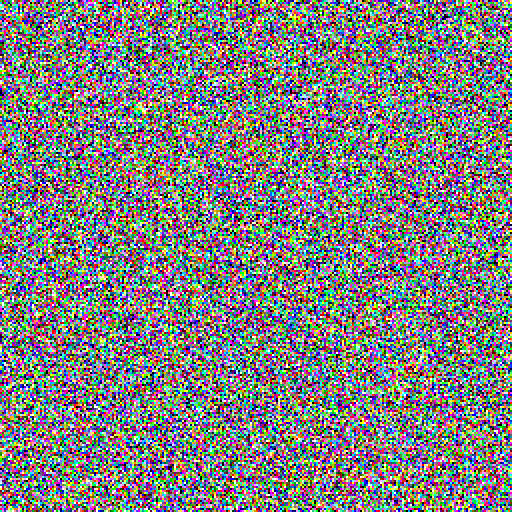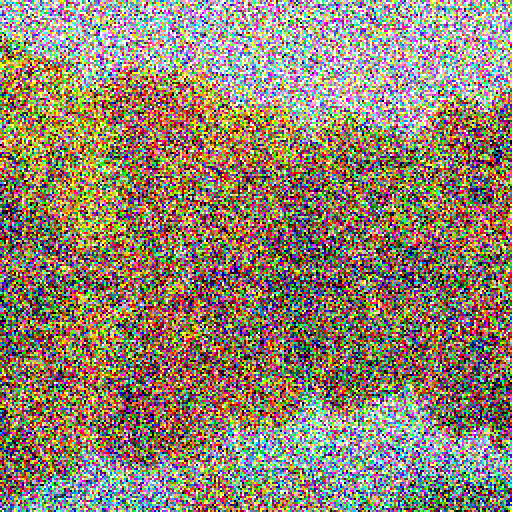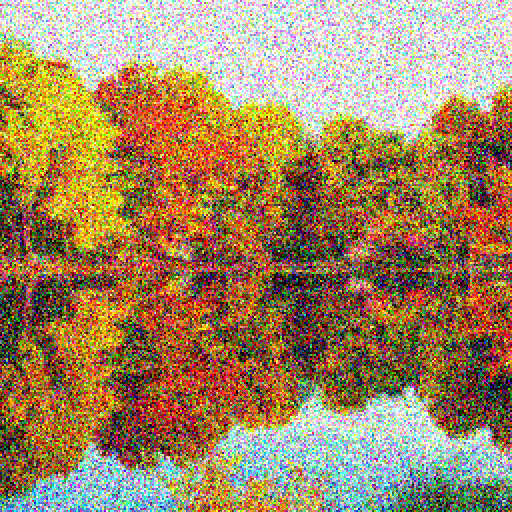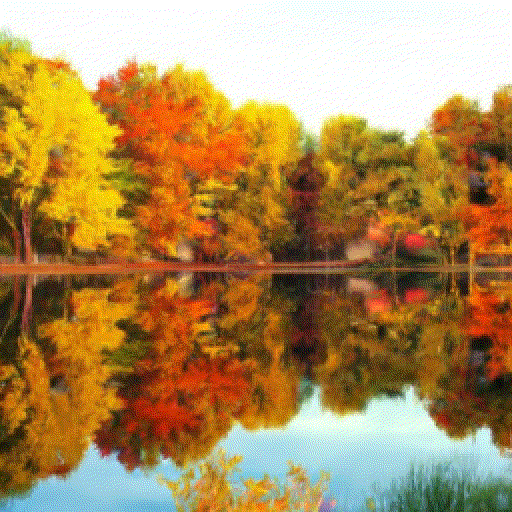Neurocomputing
Diffusion Probabilistic Models
Professur für Künstliche Intelligenz - Fakultät für Informatik
1 - Denoising Diffusion Probabilistic Model (DDPM)

Ho et al. (2020) Denoising Diffusion Probabilistic Models arXiv:2006.11239
Generative modeling
Generative modeling consists in transforming a simple probability distribution (e.g. Gaussian) into a more complex one (e.g. images).
Learning this model allows to easily sample complex images.
VAE and GAN transform simple noise into complex distributions
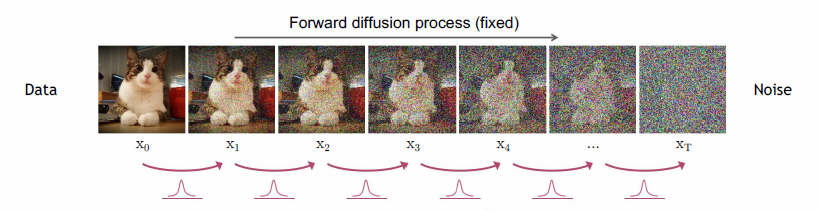
Destroying information is easier than creating it
The task of the generators in GAN or VAE is very hard: going from noise to images in a few layers.
The other direction is extremely easy.
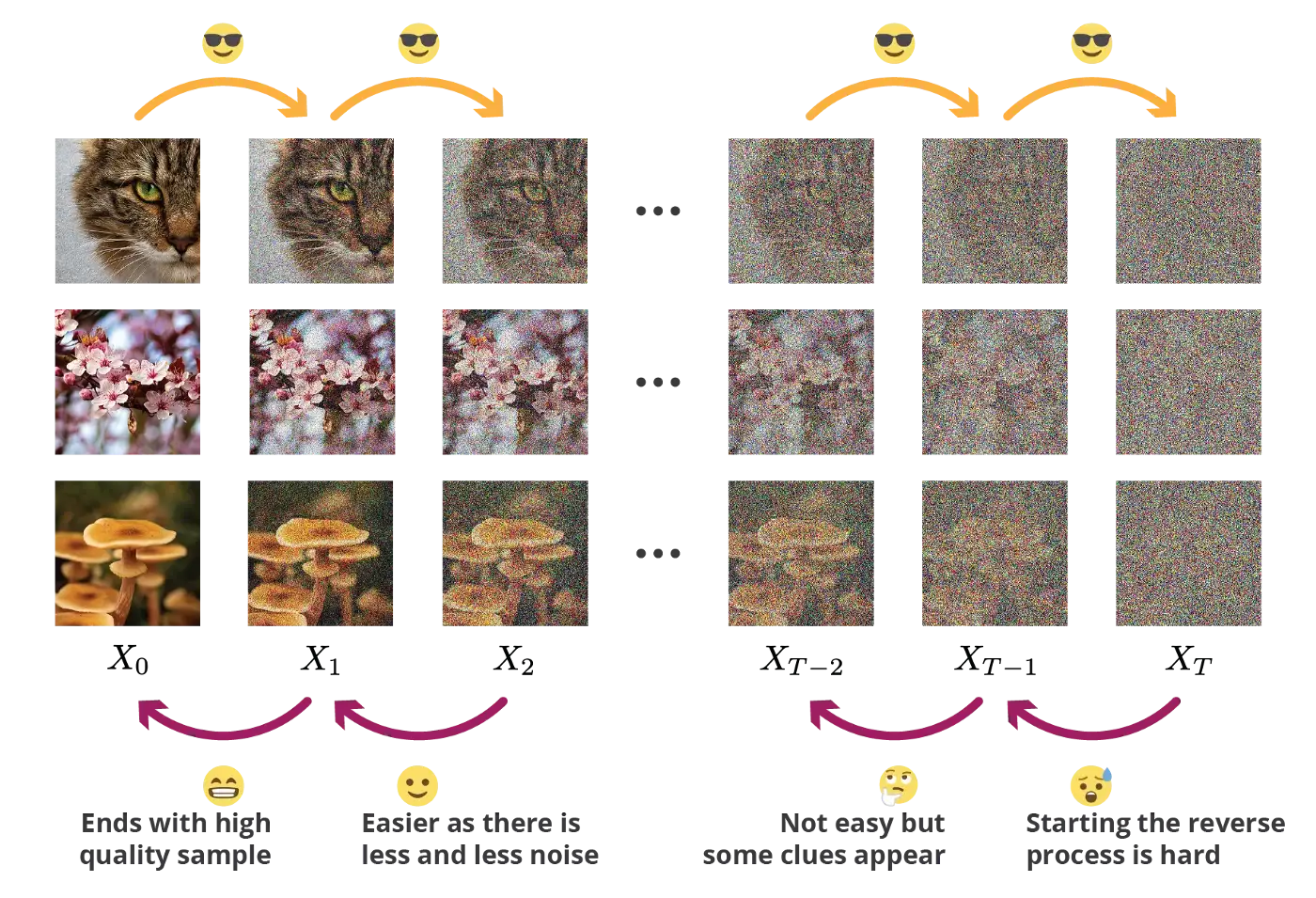
Diffusion process
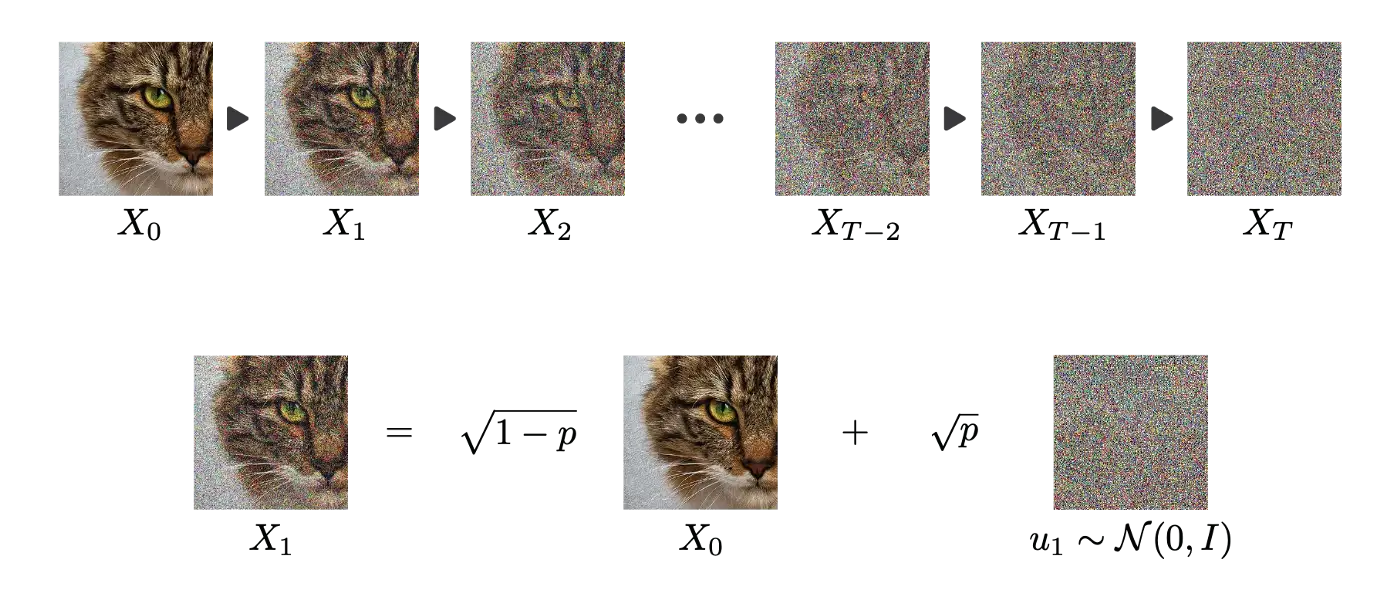
The forward diffusion process iteratively destructs all information in the image through a Markov chain that adds white noise.
A Markov chain implies that each step is independent and governed by a probability distribution q(x_t | x_{t-1}).
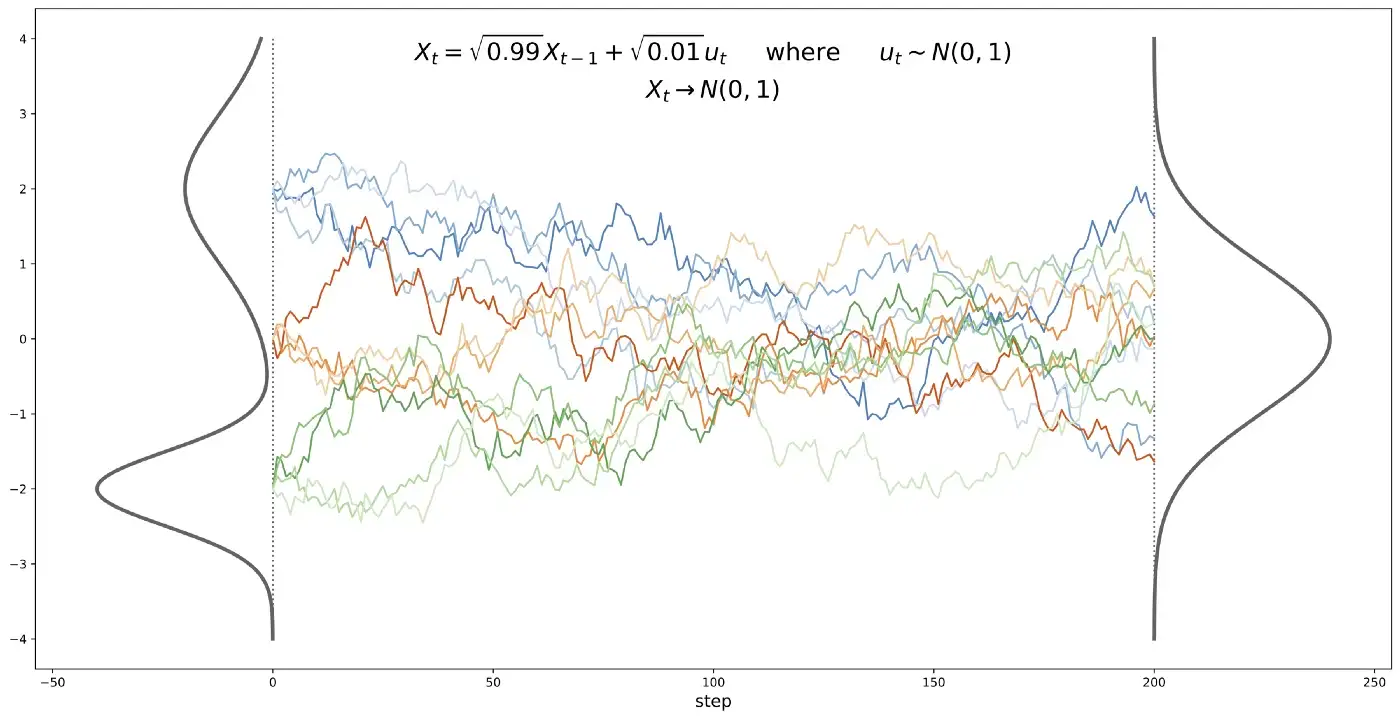
Stochastic processes can destroy information
- Iteratively adding normal noise to a signal creates a stochastic differential equation (SDE), such as the Ornstein–Uhlenbeck (OU) stochastic process.
\begin{aligned} \text{discrete:} \qquad& x_t = \sqrt{1 - \beta_t} \, x_{t-1} + \sqrt{\beta_t} \, \epsilon \\ & \qquad\qquad\text{where} \qquad \epsilon \sim \mathcal{N}(0, 1) \\ &\\ \text{continuous:} \qquad & dx = - \dfrac{1}{2} \, \beta(t) \, x \, dt + \sqrt{\beta(t)} \, dW \\ \end{aligned}
- Any probability distribution converges to a normal distribution when following the OU process.
- The Focker-Planck equation is a general form of the OU process (drift + diffusion), hence the name:
dx = \underbrace{\mu(x, t) \, dt}_{\text{drift}} + \underbrace{\sigma(x, t) \, dW}_{\text{diffusion}}
Probabilistic diffusion models
- It should be possible to reverse each diffusion step by removing the noise using a sort of denoising autoencoder.
Reminder: Denoising autoencoder
- A denoising autoencoder (DAE) is trained with noisy inputs but perfect desired outputs. It learns to suppress that noise.
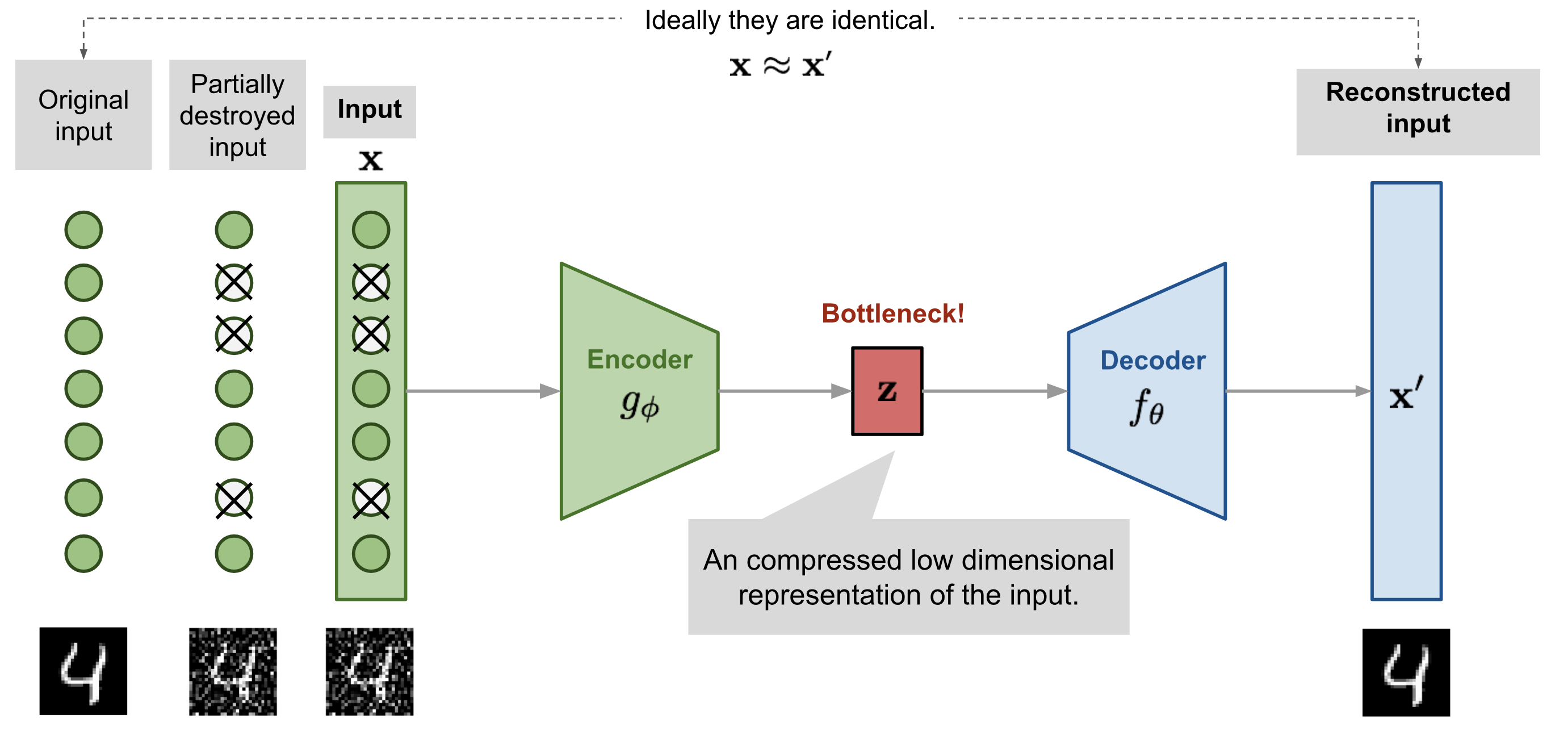
Vincent et al. (2010) “Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion”. JMLR.
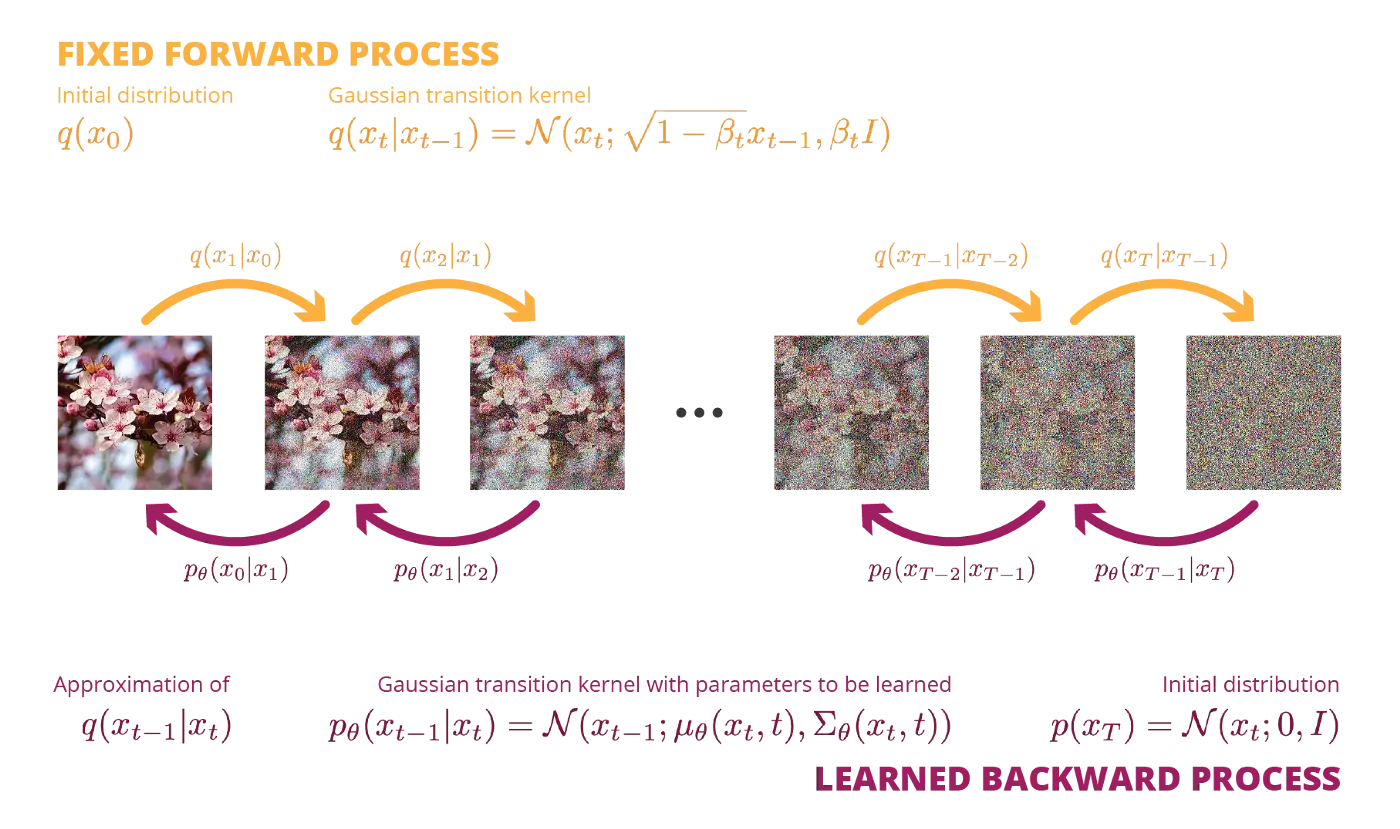
Forward Diffusion process
The forward process iteratively corrupts the image using q(x_t | x_{t-1}) for T steps (e.g. T=1000).
The goal is to learn a reverse process p_\theta(x_{t-1} | x_t) that approximates the true posterior q(x_{t-1} | x_t).
Forward Diffusion process
- The forward diffusion process iteratively adds Gaussian noise with a fixed variance schedule \beta_t:
x_t = \sqrt{1 - \beta_t} \, x_{t-1} + \sqrt{\beta_t} \, \epsilon \;\; \text{where} \; \epsilon \sim \mathcal{N}(0, I)
- It is equivalent to say that we sample x_t from a conditional normal distribution.
q(x_t | x_{t-1}) = \mathcal{N}(\mu_t = \sqrt{1 - \beta_t} \, x_{t-1}, \Sigma_t^2 = \beta_t \, I)
\mu_t = \sqrt{1 - \beta_t} \, x_{t-1} is the mean of the distribution, \Sigma_t^2 = \beta_t \, I its variance.
The parameter \beta_t is annealed with a decreasing schedule, as adding more noise at the end does not destroy much more information.
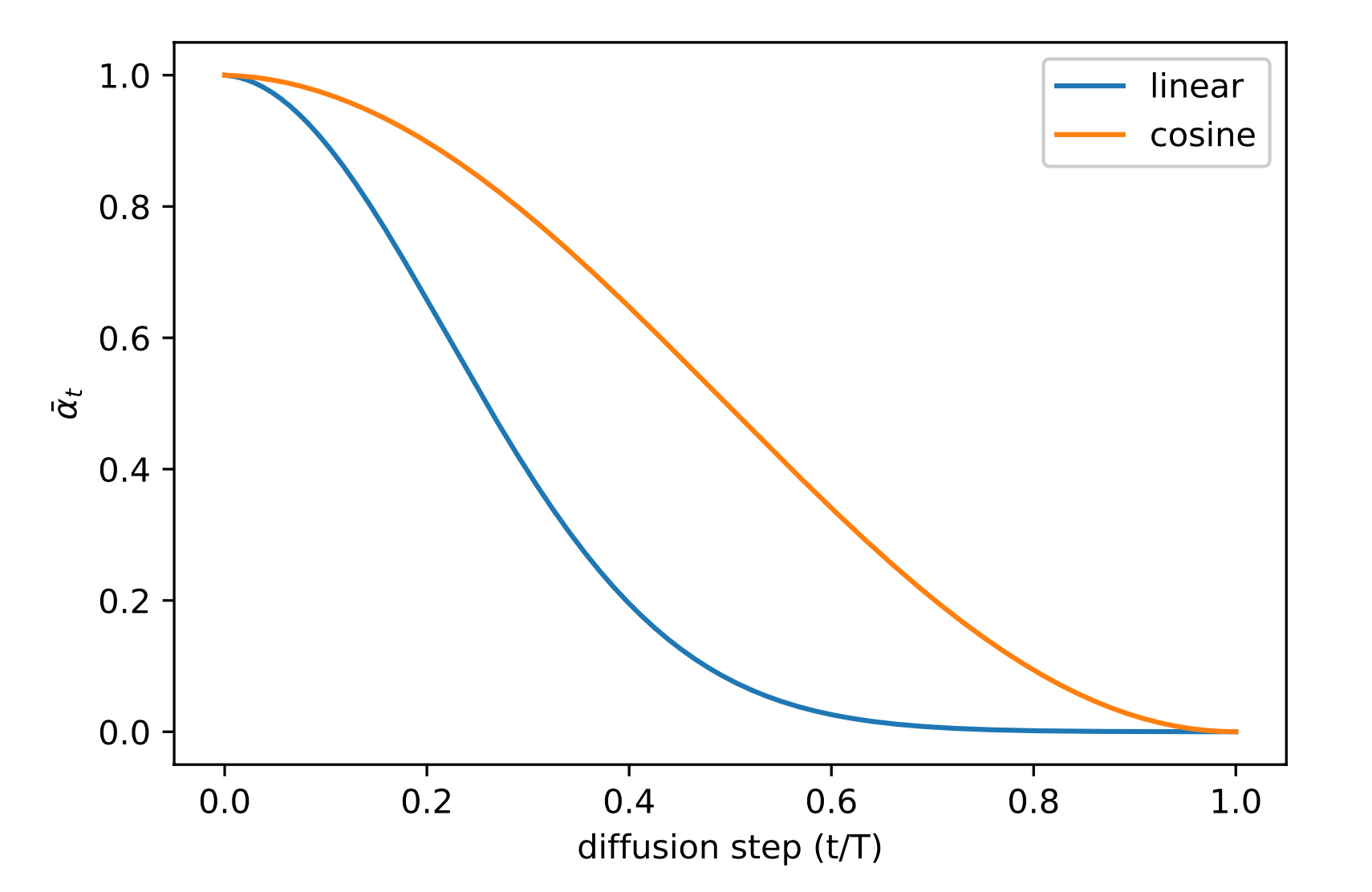
Forward Diffusion process
- Nice property: each image x_t is also a noisy version of the original image x_0:
q(x_t | x_{0}) = \mathcal{N}(\sqrt{\bar{\alpha}_t} \, x_0 , (1 - \bar{\alpha}_t) \, I) x_t = \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon_t \;\; \text{where} \; \epsilon_t \sim \mathcal{N}(0, I)
with \alpha_t = 1 - \beta_t and \bar{\alpha}_t = \prod_{s=1}^t \alpha_s only depending on the history of \beta_t.
Adding Gaussian noise to Gaussian noise is still Gaussian noise.
We do not need to perform t noising steps on x_0 to obtain x_t!
Reverse diffusion model
- The goal of the reverse diffusion process is to find a parameterized model p_\theta explaining the sequence of images backwards in time:
p_\theta(x_{0:T}) = p(x_T) \, \prod_{t=1}^T p_\theta(x_{t-1} | x_t)
where:
p_\theta(x_{t-1} | x_t) = \mathcal{N}(\mu_\theta(x_t, t), \Sigma_\theta(x_t, t))
- The reverse process is also normally distributed, given that the noise \beta_t is not too big.
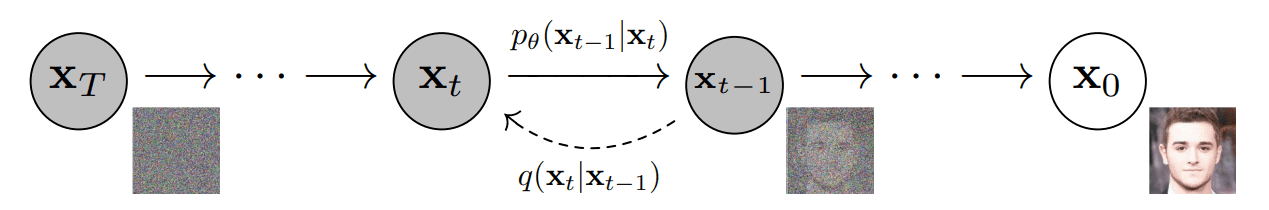
Denoising Probabilistic Diffusion Model
- By doing some Bayesian inference on the true posterior q(x_{t-1} | x_t) = \mathcal{N}(\mu_t, \Sigma_t), Ho et al. (2020) could show that:
\begin{cases} \mu_t = \dfrac{1}{\sqrt{\alpha_t}} \, (x_t - \dfrac{1-\alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \, \epsilon_t)\\ \\ \Sigma_t = \dfrac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_{t}} \beta_t \, I = \bar{\beta}_t \, I \\ \end{cases}
- The reverse variance only depends on the schedule of \beta_t, it can be pre-computed.
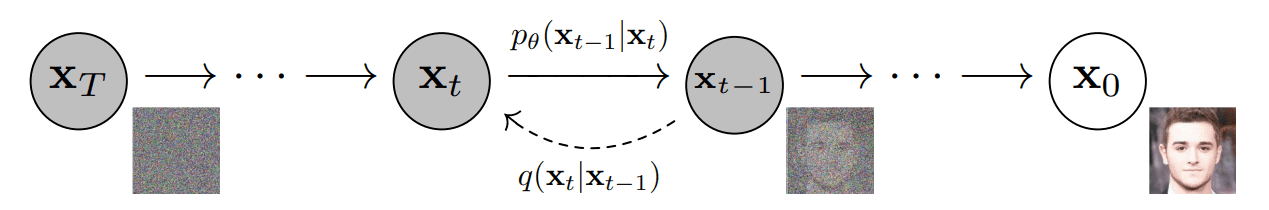
Denoising Probabilistic Diffusion Model
- The reverse model p_\theta(x_{t-1} | x_t) only need to approximate the mean:
\mu_\theta(x_t, t) = \dfrac{1}{\sqrt{\alpha_t}} \, (x_t - \dfrac{1-\alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \, \epsilon_\theta(x_t, t))
x_t is an input to the model, it does not have to predicted.
All we need to learn is the noise \epsilon_\theta(x_t, t) \approx \epsilon_t that was added to the original image x_0 to obtain x_t:
x_t = \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon_t
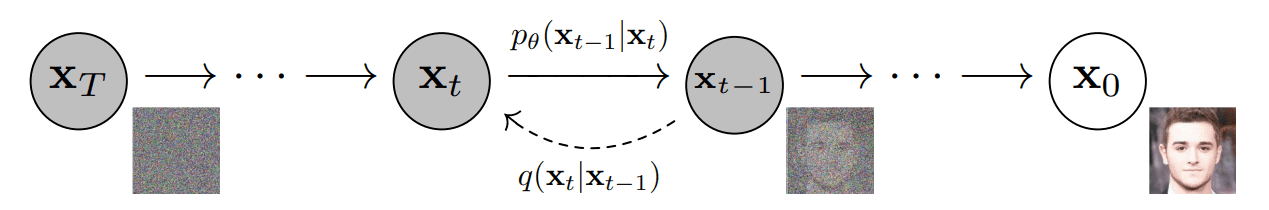
Denoising Probabilistic Diffusion Model
- We want to predict the added noise in the image space:
\epsilon_\theta(x_t, t) = \epsilon_\theta(\sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon_t, t) \approx \epsilon_t
- We can simply minimize the mse with the true noise:
\begin{aligned} \mathcal{L}(\theta) &= \mathbb{E}_{t \sim [1, T], x_0, \epsilon_t} [(\epsilon_t - \epsilon_\theta(x_t, t))^2] \\ &= \mathbb{E}_{t \sim [1, T], x_0, \epsilon_t} [(\epsilon_t - \epsilon_\theta(\sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon_t, t) )^2] \\ \end{aligned}
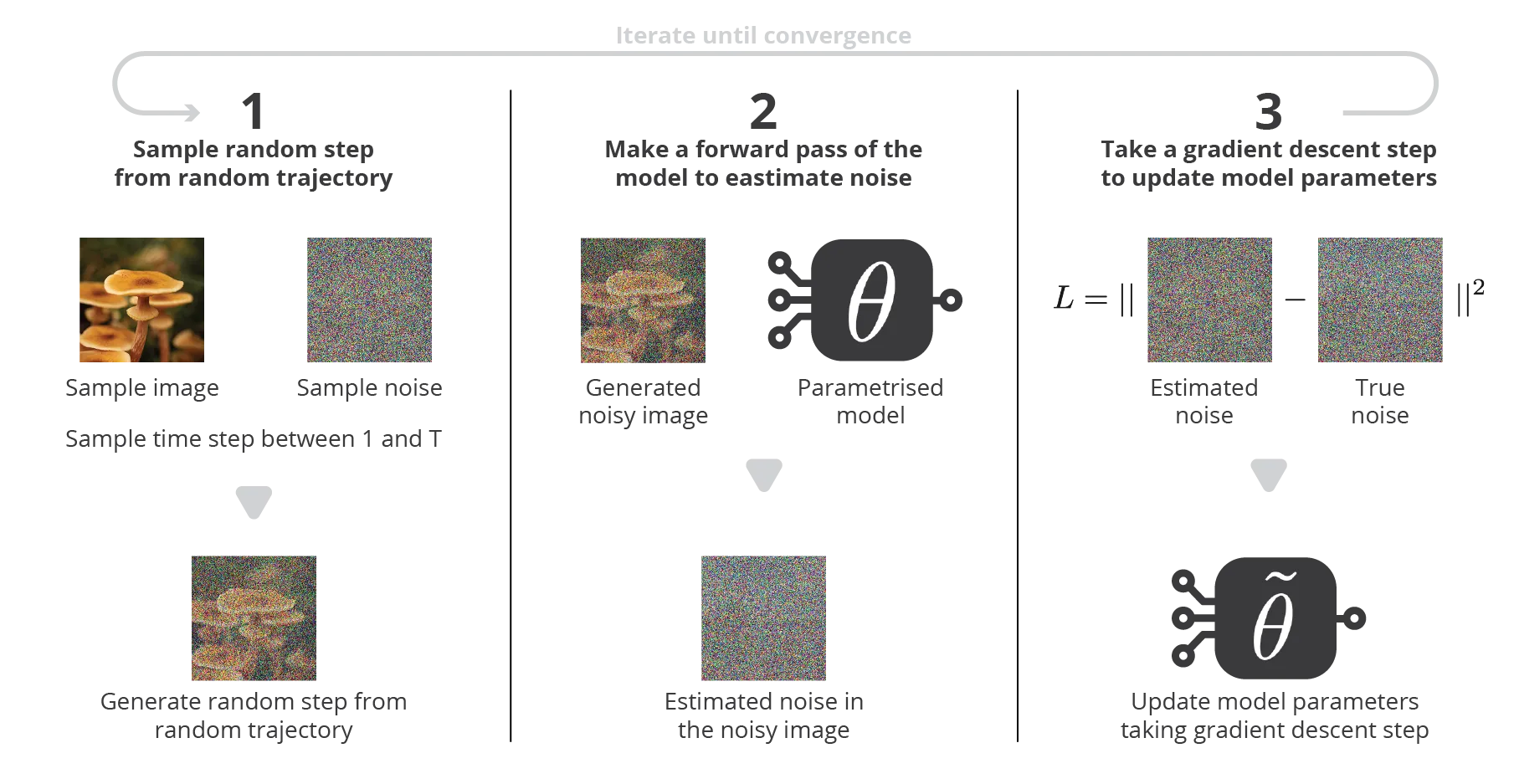
- We only need to sample an image x_0, a time step t, a noise \epsilon_t \sim \mathcal{N}(0, I), predict the noise \epsilon_\theta(x_t, t) and minimize the mse!

Ho et al. (2020) Denoising Diffusion Probabilistic Models. arXiv:2006.11239
Denoising Probabilistic Diffusion Model
- Training can be done on individual samples, no need for the whole Markov chain to create the minibatches.
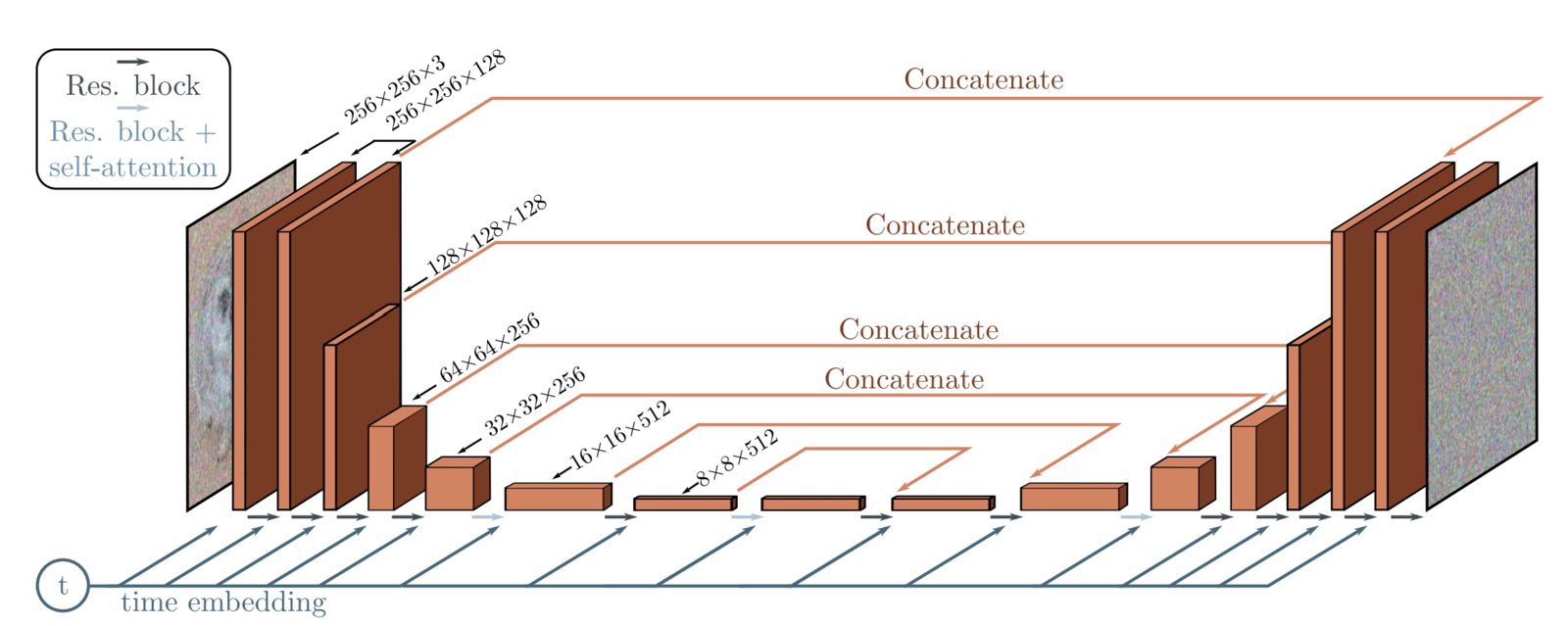
DDPM backbone
- The neural network used for the reverse diffusion is usually some kind of U-net, with attentional layers, or even a vision Transformer.
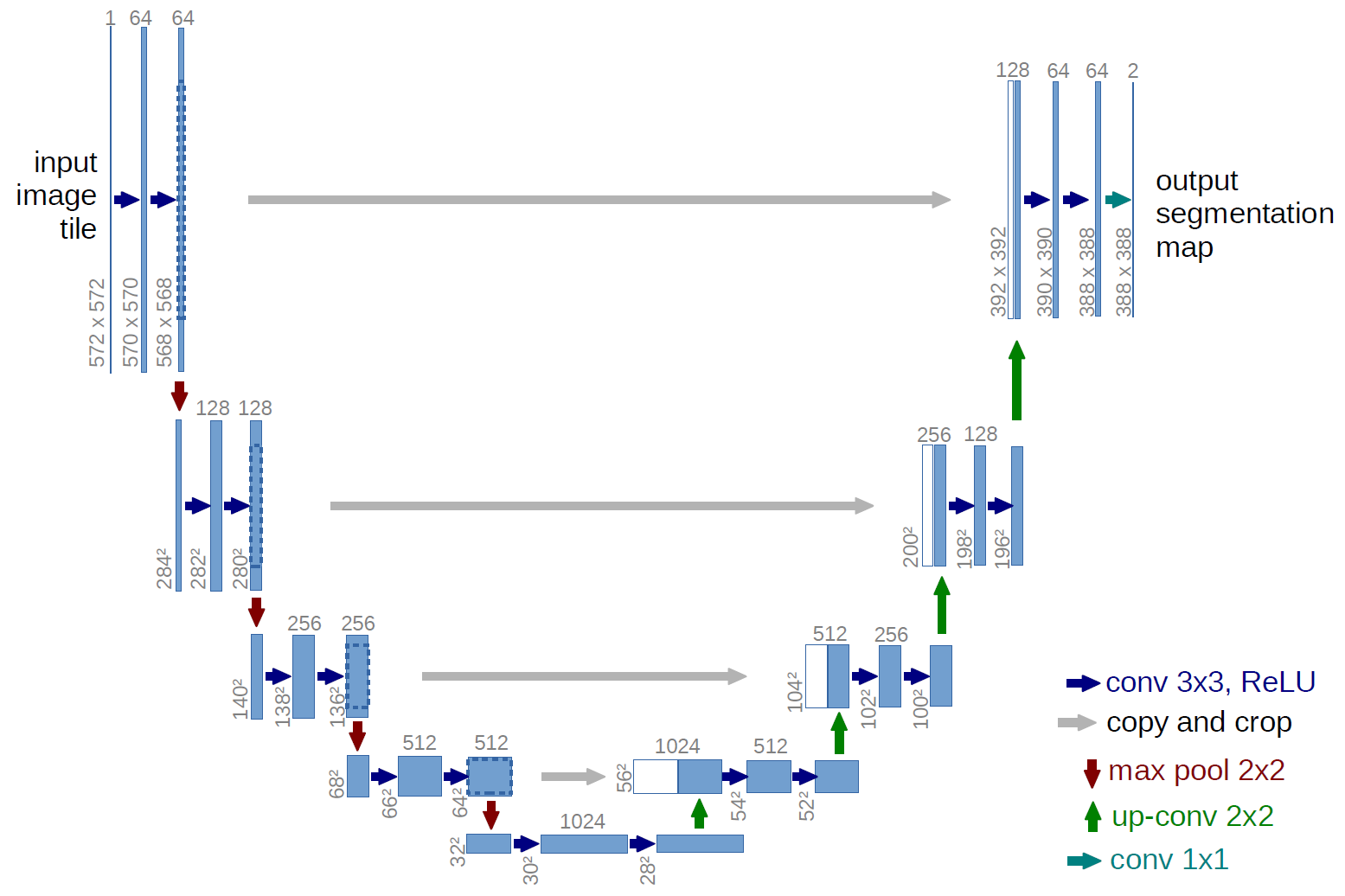
- A time embedding for the time index t is necessary. It is usually added to each layer of the U-Net.
DDPM sampler
- The reverse diffusion occurs iteratively backwards in time (1000 steps) by sampling the posterior:
p_\theta(x_{t-1} | x_t) = \mathcal{N}(\mu_\theta(x_t, t), \bar{\beta}_t \, I)
x_{t-1} = \dfrac{1}{\sqrt{\alpha_t}} \, (x_t - \dfrac{1-\alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \, \epsilon_\theta(x_t, t)) + \bar{\beta}_t \, \epsilon
The last step x_1 \rightarrow x_0 can be done deterministically.
It is possible to use less iterations (200) by taking bigger steps, but this stays expensive and generates lower quality images.
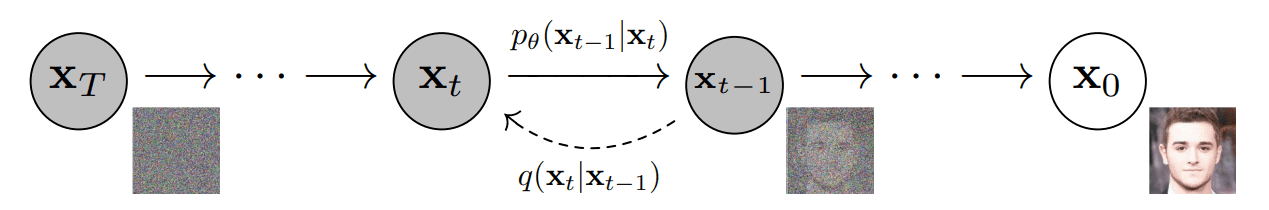
Denoising Probabilistic Diffusion Model
Modern samplers
- The equivalent SDE is:
dx = \left[-\frac{1}{2}\beta(t) x + \frac{\beta(t)}{\sqrt{1-\bar{\alpha}_t}} \epsilon_\theta(x, t)\right] dt + \sqrt{\beta(t)} \, d\bar{W}
- The DDPM sampler is actually a simple first-order Euler-Maruyama SDE solver:
x_{t-1} = \dfrac{1}{\sqrt{\alpha_t}} \, (x_t - \dfrac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \, \epsilon_\theta(x_t, t)) + \bar{\beta}_t \, \epsilon
- Higher-order and/or deterministic solvers allow to more precisely evaluate the SDE while taking much less steps (50), such as the DDIM sampler, or fancier ones like DPM++, Heun, etc.
x_{t-1} = \sqrt{\bar{\alpha}_{t-1}} \, (\dfrac{x_t - \sqrt{1- \bar{\alpha}_t} \, \epsilon_\theta(x_t, t)}{ \sqrt{\bar{\alpha}_t}}) + \sqrt{1 - \bar{\alpha}_{t-1}} \, \epsilon_\theta(x_t, t)
2 - Loss derivation
Loss derivation
Let’s now see how to arrive to the same loss function from a variational point of view.
The blog post by Lilian Weng is very helpful: https://lilianweng.github.io/posts/2021-07-11-diffusion-models/, as well as this one by Jonathan Kernes https://towardsdatascience.com/diffusion-models-91b75430ec2.
As we have a generative model (learning the distribution of images x_0), all we want to maximize is the log-likelihood of the model p_\theta(x_0) on the data, which gives us the following NLL loss:
\mathcal{L}(\theta) = \mathbb{E}_{x_0 \sim q(x_0)} [- \log p_\theta(x_0)] = \int - q(x_0) \log p_\theta(x_0) dx_0
Loss derivation
The first trick is to rewrite the log-evidence \log p_\theta(x_0) as a function of normalized transition probabilities using the Markov assumption.
Let’s first marginalize p_\theta(x_0) using the rest of the sequence (x_1, \ldots x_T), involving the joint probability of the sequence:
\log p_\theta(x_0) = \log \int p_\theta(x_0, x_1, \ldots, x_T)\, dx_1 \, dx_2 \ldots \, dx_T
- The Markov assumption states that the different denoising steps of the sequence are independent from each other, i.e. x_t contains enough information to predict the distribution of x_{t-1}, there is no need to know the “history”, i.e. the other steps:
p_\theta(x_0, x_1, \ldots, x_T) = p_\theta(x_T) \prod_{t=1}^T p_\theta(x_{t-1} | x_t)
Loss derivation
- Let’s do the same with the forward process on the whole sequence q(x_0, x_1, \ldots x_t), but in the other direction:
q(x_0, x_1, \ldots, x_T) = q(x_0) \prod_{t=1}^T q(x_{t} | x_{t-1})
- Dividing both sides with q(x_0), we obtain the conditional:
q(x_1, \ldots, x_T | x_0) = \prod_{t=1}^T q(x_{t} | x_{t-1})
- Noting dx_{1..T} = dx_1 \, dx_2 \ldots \, dx_T, we have
\log p_\theta(x_0) = \log \int p_\theta(x_T) \prod_{t=1}^T p_\theta(x_{t-1} | x_t) \, dx_{1..T}
Loss derivation
- We now use the importance sampling trick, by adding the term \dfrac{q(x_1, \ldots, x_T | x_0)}{q(x_1, \ldots, x_T | x_0)} = 1 inside the equation and expanding the denominator:
\begin{aligned} \log p_\theta(x_0) & = \log \int \dfrac{q(x_1, \ldots, x_T | x_0)}{q(x_1, \ldots, x_T | x_0)} p_\theta(x_T) \prod_{t=1}^T p_\theta(x_{t-1} | x_t) \, dx_{1..T} \\ &\\ &= \log \int q(x_1, \ldots, x_T | x_0) \, p_\theta(x_T) \prod_{t=1}^T \frac{p_\theta(x_{t-1} | x_t)}{q(x_t | x_{t-1})} \, dx_{1..T} \\ &\\ &= \log \mathbb{E}_{x_1, \dots, x_T \sim q(x_1, \ldots, x_T | x_0)} [ p_\theta(x_T) \prod_{t=1}^T \frac{p_\theta(x_{t-1} | x_t)}{q(x_t | x_{t-1})} ] \\ \end{aligned}
The importance sampling trick is a brilliant way to replace pesky integrals with expectations, which can later be sampled. This is exactly the same trick as in RL and policy gradients.
What this expectation means is that we only need to sample the sequence x_1, \ldots, x_t conditioned on x_0 (the input image) following the forward process.
Loss derivation
- We now use Jensen’s inequality (\mathbb{E}[f(X)] \geq f(\mathbb{E}[X]) if f is convex) to put the log inside the expectation and obtain a lower bound on the log-evidence:
\begin{aligned} \log p_\theta(x_0) &\geq \mathbb{E}_{x_1, \dots, x_T \sim q(x_1, \ldots, x_T | x_0)} [ \log ( p_\theta(x_T) \prod_{t=1}^T \frac{p_\theta(x_{t-1} | x_t)}{q(x_t | x_{t-1})} )] \\ &\\ &= \mathbb{E}_{x_1, \dots, x_T \sim q(x_1, \ldots, x_T | x_0)} [ \log p_\theta(x_T) + \sum_{t=1}^T \log \frac{p_\theta(x_{t-1} | x_t)}{q(x_t | x_{t-1})} ] \\ &\\ &= \text{ELBO}(p_\theta, q, x_0) \end{aligned}
The evidence lower bound (ELBO) or variational lower bound (VLB) is a classical trick in variational inference (including VAE): the goal is to maximize the evidence \log p_\theta(x_0), but it is generally intractable.
We instead maximize its lower bound, as the parameters \theta maximizing the ELBO will also maximize the evidence (see https://yunfanj.com/blog/2021/01/11/ELBO.html for more details).
Loss derivation
The ratio of probabilities \log \dfrac{p_\theta(x_{t-1} | x_t)}{q(x_t | x_{t-1})} looks interesting, as it might lead us to a KL divergence, but the conditionals are reversed.
Let’s use the Bayes rule to invert q(x_t | x_{t-1}), remembering from earlier that it is only tractable when conditioned on x_0:
q(x_{t}| x_{t-1}) = q(x_{t}| x_{t-1}, x_0) = q(x_{t-1}| x_{t}, x_0) \, \dfrac{q(x_{t} | x_0)}{q(x_{t-1} | x_0)}
- The first equality q(x_{t}| x_{t-1}) = q(x_{t}| x_{t-1}, x_0) is due to the Markov property, we do not need x_0 to predict x_{t} from x_{t-1} in the forward process!
Loss derivation
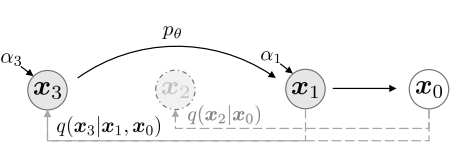
- Let’s plug this in our ELBO, taking out t=1 from the sum:
\begin{aligned} \log p_\theta(x_0) &\geq \mathbb{E}_{x_1, \dots, x_T \sim q(x_1, \ldots, x_T | x_0)} [ \log p_\theta(x_T) + \sum_{t=2}^T \log \frac{p_\theta(x_{t-1} | x_t)}{q(x_t | x_{t-1})} + \log \dfrac{p_\theta(x_0 | x_1)}{q(x_1 | x_0)}] \\ &\\ &= \mathbb{E}_{x_1, \dots, x_T \sim q(x_1, \ldots, x_T | x_0)} [ \log p_\theta(x_T) + \sum_{t=2}^T \log \frac{p_\theta(x_{t-1} | x_t)}{q(x_{t-1} | x_{t}, x_0)} \, \dfrac{q(x_{t-1} | x_0)}{q(x_t | x_0)}+ \log \dfrac{p_\theta(x_0 | x_1)}{q(x_1 | x_0)}] \\ &\\ &= \mathbb{E}_{x_1, \dots, x_T \sim q(x_1, \ldots, x_T | x_0)} [ \log p_\theta(x_T) + \sum_{t=2}^T \log \frac{p_\theta(x_{t-1} | x_t)}{q(x_{t-1} | x_{t}, x_0)} + \sum_{t=2}^T \log \dfrac{q(x_{t-1} | x_0)}{q(x_t | x_0)} + \log \dfrac{p_\theta(x_0 | x_1)}{q(x_1 | x_0)}] \\ \end{aligned}
- The term \sum_{t=2}^T \log \dfrac{q(x_{t-1} | x_0)}{q(x_t | x_0)} cancels nicely and becomes equal to \log q(x_1 | x_0) - \log q(x_{T} | x_0).
Loss derivation
- The first term \log q(x_1 | x_0) even cancels the denominator of \log \dfrac{p_\theta(x_0 | x_1)}{q(x_1 | x_0)}, so we obtain:
\begin{aligned} \log p_\theta(x_0) &\geq \mathbb{E}_{x_1, \dots, x_T \sim q(x_1, \ldots, x_T | x_0)} [ \log p_\theta(x_T) + \sum_{t=2}^T \log \frac{p_\theta(x_{t-1} | x_t)}{q(x_{t-1} | x_{t}, x_0)} -\log q(x_T | x_0) + \log p_\theta(x_0 | x_1) ] \\ &\\ & = \mathbb{E}_{x_1, \dots, x_T \sim q(x_1, \ldots, x_T | x_0)} [ \log \dfrac{p_\theta(x_T)}{q(x_T | x_0)} + \sum_{t=2}^T \log \frac{p_\theta(x_{t-1} | x_t)}{q(x_{t-1} | x_{t}, x_0)} + \log p_\theta(x_0 | x_1) ]\\ &\\ & = \mathbb{E}_{x_1, \dots, x_T \sim q(x_1, \ldots, x_T | x_0)} [ L_T + \sum_{t=2}^T L_{t} + L_0 ]\\ \end{aligned}
Loss derivation
\begin{aligned} \log p_\theta(x_0) & = \mathbb{E}_{x_1, \dots, x_T \sim q(x_1, \ldots, x_T | x_0)} [ L_T + \sum_{t=2}^T L_{t} + L_0 ]\\ \end{aligned}
- The final term L_T depends on the final image x_T, which is just pure noise if the forward process was parameterized correctly. The reverse process does not play a role in obtaining x_T, so it is a constant with respect to \theta, and we can ignore it for the optimization process.
- The initial loss L_0 = \log p_\theta(x_0 | x_1) concerns the reconstruction of the original image from the first noisy version. It ensures that the model can accurately recover the original data after the noise has been gradually removed through the reverse process. It is in particular involved in scaling the pixels to [-1,1], ensuring that a real image comes out of the denoising process.
- The loss at time t L_t = \log \dfrac{p_\theta(x_{t-1} | x_t)}{q(x_{t-1} | x_{t}, x_0)} = - \text{KL} (p_\theta(x_{t-1} | x_t), q(x_{t-1} | x_{t}, x_0)) is the KL divergence between the learned posterior p_\theta(x_{t-1} | x_t) and the “true” posterior q(x_{t-1} | x_{t}, x_0).
Loss derivation
- Now we can simplify this loss using all our assumptions. In particular, the Markov property states that the different step of the noising/denoising process are independent, so we do no need to explicitly optimize the sum of all L_t terms: optimizing each of them individually by sampling t uniformly in [1, T] would lead to the same result.
\mathcal{L}_\text{VLB}(\theta) = \mathbb{E}_{x_0 \sim q(x_0), t \sim \mathcal{U}(1, T)} [\text{KL} (p_\theta(x_{t-1} | x_t), q(x_{t-1} | x_{t}, x_0) ) ]
Remember that L_T does not matter, and that L_0 will be a special case. We call this loss the variational lower bound VLB.
Moreover, we know that both distributions inside the KL are normal distributions. As shown earlier, the true posterior is known to be:
q(x_{t-1}| x_t, x_0) = \mathcal{N}(x_{t-1}; \hat{\mu}(x_t, t) = \dfrac{1}{\sqrt{\bar{\alpha}_t}} \, (x_t - \dfrac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \, \epsilon_t), (\dfrac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \, \beta_t)^2 \, I)
- The learned posterior should therefore also be a normal distribution, whose parameters should be learned.
p_\theta(x_{t-1}| x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma^2_\theta(x_t, t))
Loss derivation
- The interest of having normal distributions is that their KL divergence takes a closed form:
Closed form of the KL divergence between two Gaussians
The closed form of the KL divergence between X = \mathcal{N}(\mu_x, \sigma^2_x) and Y=\mathcal{N}(\mu_y, \sigma^2_y) is simply a function of their parameters:
\text{KL}(X ||Y) = \log \dfrac{\sigma_y}{\sigma_x} + \dfrac{\sigma_x^2 + (\mu_x - \mu_y)^2}{2 \sigma_y^2} - \dfrac{1}{2}
Loss derivation
Furthermore, an assumption of DDPM is that the variance schedule \beta_t is fixed and does not depend on \theta.
All terms of the KL depending on the variances disappear when calculating the gradient of the KL.
All that remains in the loss function is the squared difference between the means, i.e. the mse!
\mathcal{L}_\text{VLB}(\theta) = \mathbb{E}_{x_0 \sim q(x_0), t \sim \mathcal{U}(1, T)} [ (\hat{\mu}(x_t, t) - \mu_\theta(x_t, t))^2 ]
Loss derivation
- In addition, noting that \hat{\mu}(x_t, t) = \dfrac{1}{\sqrt{\bar{\alpha}_t}} \, (x_t - \dfrac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \, \epsilon_t), we can parameterize \mu_\theta(x_t, t) in the following way:
\mu_\theta(x_t, t) = \dfrac{1}{\sqrt{\bar{\alpha}_t}} \, (x_t - \dfrac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \, \epsilon_\theta(x_t, t))
and have only to compute the mse between the residuals \epsilon_t and \epsilon_\theta(x_t, t). This is the simple objective we used previously:
\mathcal{L}(\theta) = \mathbb{E}_{x_0 \sim q, \epsilon_t \sim \mathcal{N}(0, I), t \sim \mathcal{U}(1, T)} [(\epsilon_t - \epsilon_\theta(x_t, t))^2]
- Using the Markov property, normal distributions, a fixed variance schedule and a clever reparameterization, we moved from the very complex ELBO loss to a simple regression on the residuals.
3 - Dall-e 2

Ramesh et al. (2022) Hierarchical Text-Conditional Image Generation with CLIP Latents. arXiv:2204.06125
Dall-e 2
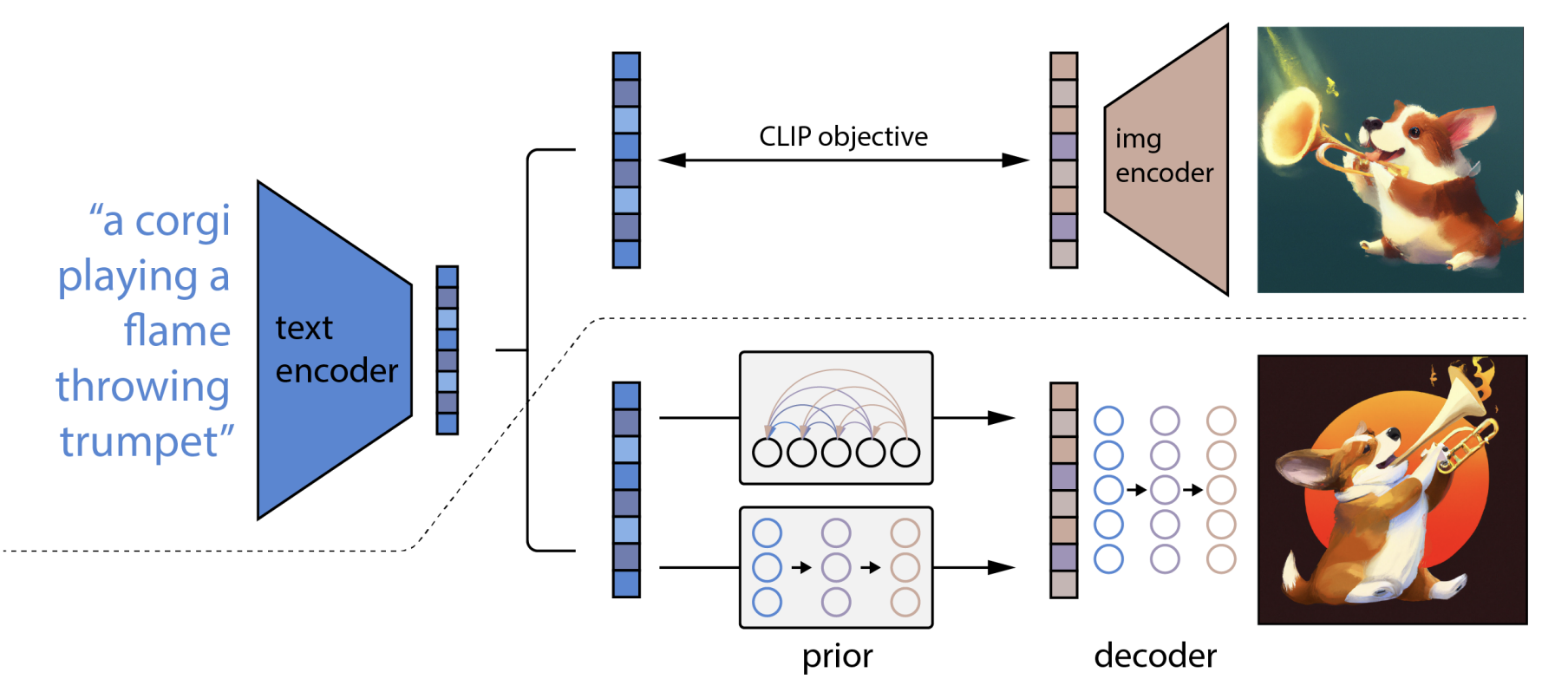
Text-to-image generators such as Dall-e, Midjourney, or Stable Diffusion combine LLM for text embedding with diffusion models for image generation.
CLIP embeddings of texts and images are first learned using contrastive learning.
A conditional diffusion process (GLIDE) then uses the image embeddings to produce images.
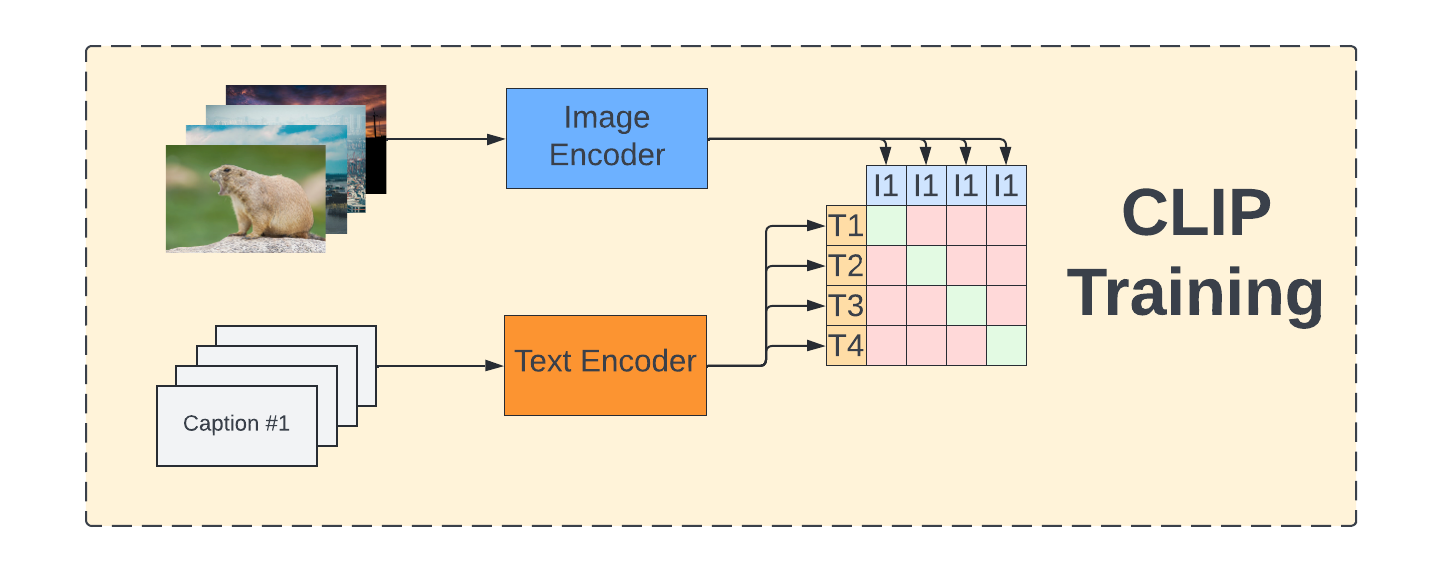
CLIP: Contrastive Language-Image Pre-training
Embeddings for text and images are learned using Transformer encoders and contrastive learning.
For each pair (text, image) in the training set, their representation should be made similar, while being different from the others.
GLIDE
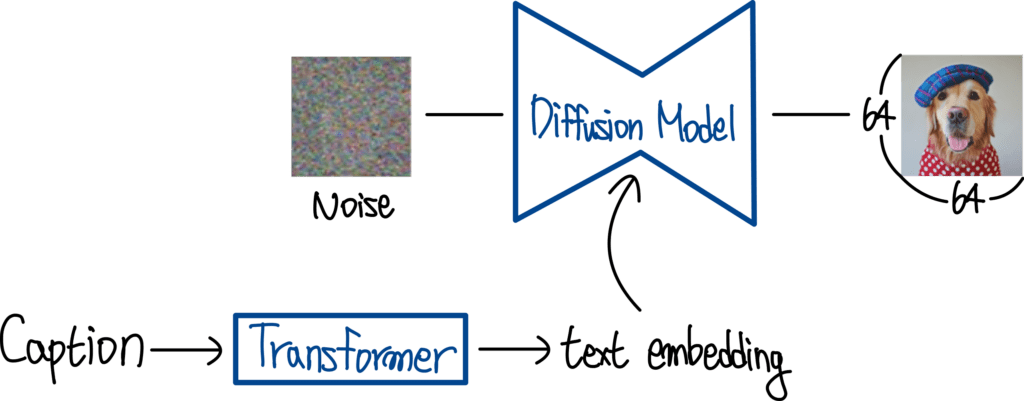
DDPMs generate images from raw noise, but there is no control over which image will emerge.
GLIDE (Guided Language to Image Diffusion for Generation and Editing) is a DDPM conditioned on a latent representation of a caption c.
As for cGAN and cVAE, the caption c is provided to the learned model:
\epsilon_\theta(x_t, t, c) \approx \epsilon_t
- Text embeddings can be obtained from any NLP model, for example a Transformer.
Nichol et al. (2022) GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models. arXiv:2112.10741
Dall-e 2
- In Dall-e 2, the prior network learns to map text embeddings to a sequence of image embeddings:
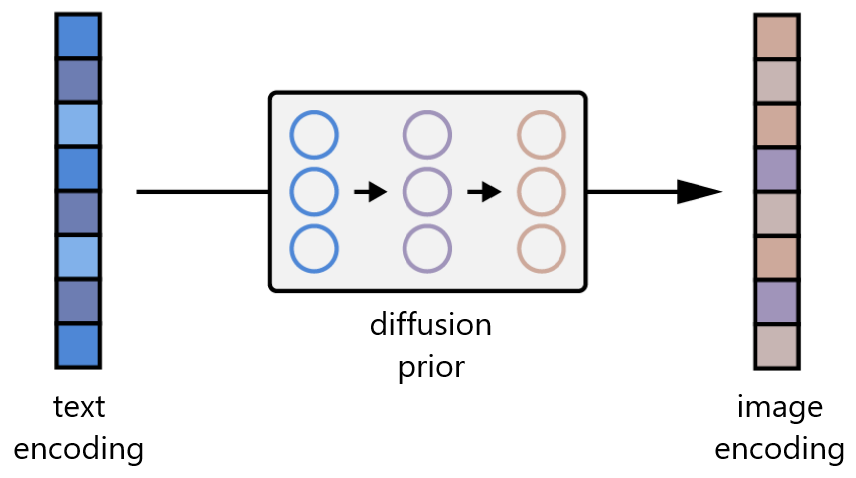
After CLIP training, the two embeddings are already close from each other, but the authors find that the diffusion process works better when the image embeddings change during the diffusion.
The image embedding is then used as the condition for GLIDE.
Ramesh et al. (2022) Hierarchical Text-Conditional Image Generation with CLIP Latents. arXiv:2204.06125