Neurocomputing
Hopfield networks
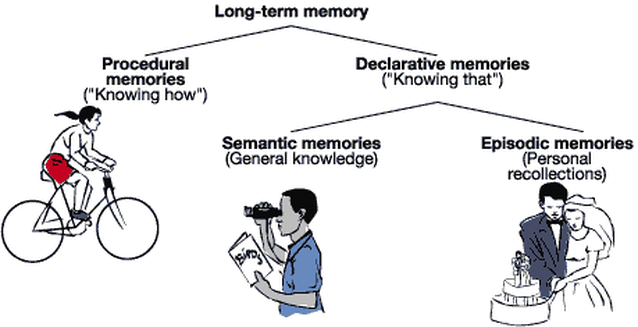
Procedural vs. episodic memory
In deep learning, our biggest enemy was overfitting, i.e. learning by heart the training examples.
But what if it was actually useful in cognitive tasks?
Deep networks implement a procedural memory: they know how to do things.
A fundamental aspect of cognition is episodic memory: remembering when specific events happened.
When can episodic memory be useful?
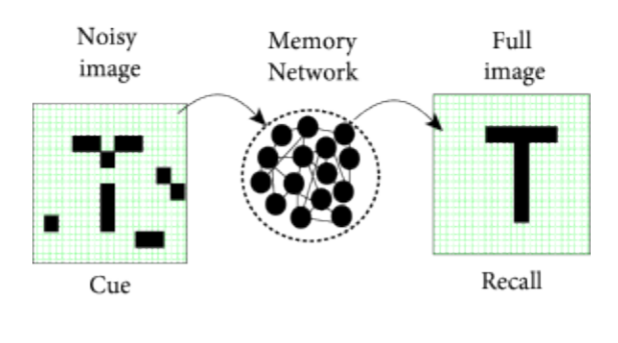
Episodic memory is particularly useful when retrieving memories from degraded or partial inputs.
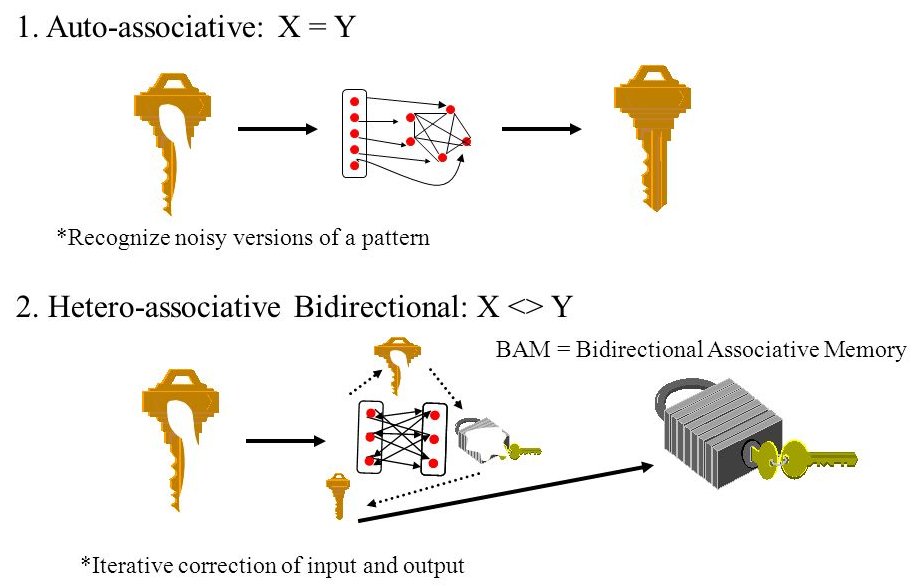
When the reconstruction is similar to the remembered input, we talk about auto-associative memory.
An item can be retrieved by just knowing part of its content: content-adressable memory.
Auto-associative memory
The classical approach is the nearest neighbour algorithm.
One compares a new input to each of the training examples using a given metric (distance) and assigns the input to the closest example.
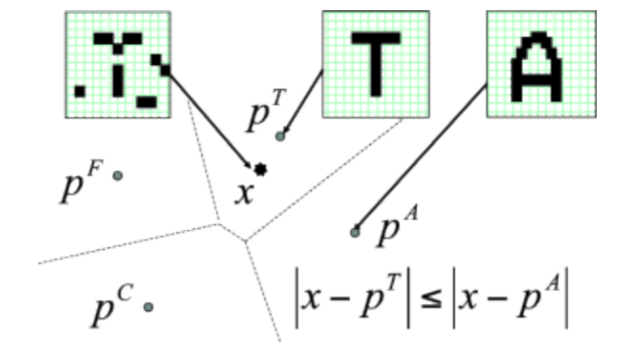
- Another approach is to have a recurrent neural network memorize the training examples and retrieve them given the input.
Hetero-associative memory
When the reconstruction is different from the input, it is an hetero-associative memory.
Hetero-associative memories often work in both directions (bidirectional associative memory):
- name \leftrightarrow face.
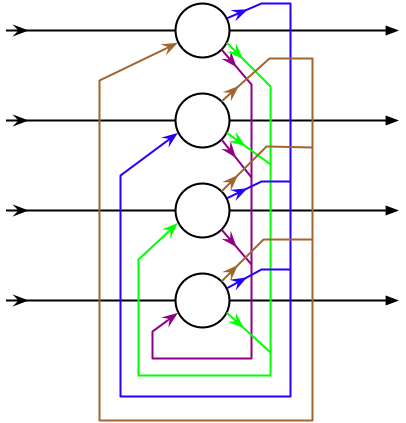
Hopfield networks
- Hopfield networks (Hopfield, 1982; Hopfield et al., 1983) only depend on a single input (one constant value per neuron) and their previous output using recurrent weights:
\mathbf{y}_t = f(\mathbf{x} + W \times \mathbf{y}_{t-1} + \mathbf{b})
For a single constant input \mathbf{x}, one lets the network converge for enough time steps T and observe what the final output \mathbf{y}_T is.
Hopfield network have their own dynamics: the output evolves over time, but the input is constant.
One can even omit the input \mathbf{x} and merge it with the bias \mathbf{b}: the dynamics will only depend on the initial state \mathbf{y}_0.
\mathbf{y}_t = f(W \times \mathbf{y}_{t-1} + \mathbf{b})
Hopfield networks
Binary Hopfield networks use binary units.
The neuron i has a net activation x_i (potential) depending on the other neurons j through weights w_{ji}:
x_i = \sum_{j \neq i} w_{ji} \, y_j + b
- The output y_i is the sign of the potential:
y_i = \text{sign}(x_i)
\text{sign}(x) = \begin{cases} +1 \; \text{if} \, x>0 \\ -1 \; \text{otherwise.}\end{cases}
There are no self-connections: w_{ii} = 0.
The weights are symmetrical: w_{ij} = w_{ji}.
- In matrix-vector form:
\mathbf{y} = \text{sign}(W \times \mathbf{y} + \mathbf{b})
Hopfield networks
At each time step, a neuron will flip its state if the sign of the potential x_i = \sum_{j \neq i} w_{ji} \, y_j + b does not match its current output y_i.
This will in turn modify the potential of all other neurons, who may also flip. The potential of that neuron may change its sign, so the neuron will flip again.
After a finite number of iterations, the network reaches a stable state (proof later).
Neurons are evaluated one after the other: asynchronous evaluation.
Hopfield networks
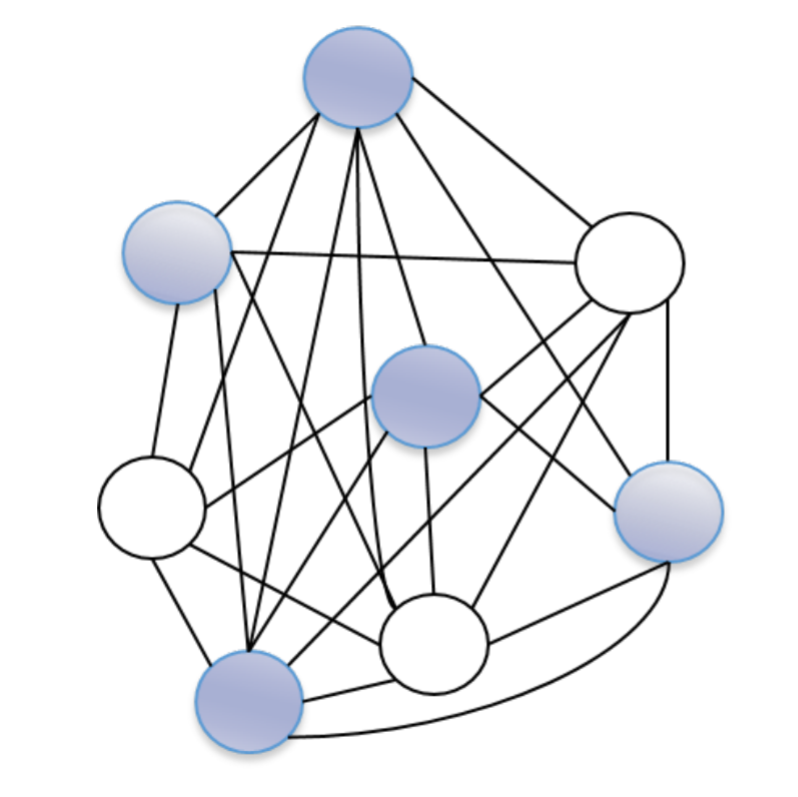
Let’s consider a Hopfield network with 5 neurons, sparse connectivity and no bias.
In the initial state, 2 neurons are on (+1), 3 are off (-1).
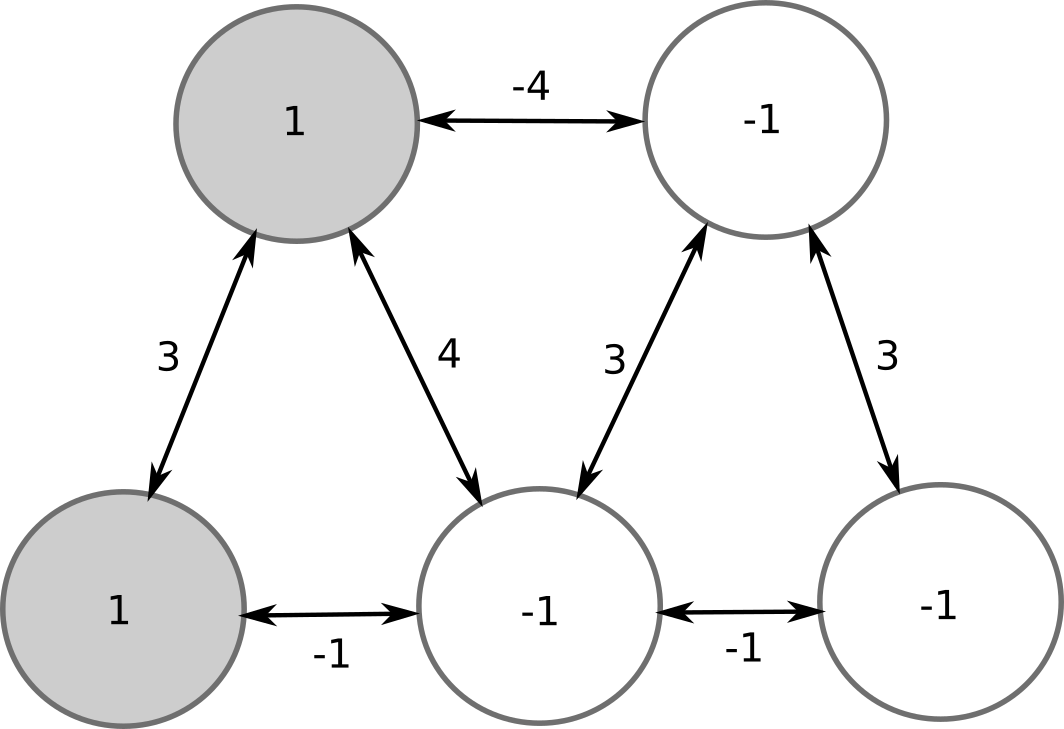
Hopfield networks
Let’s evaluate the top-right neuron.
Its potential is -4 * 1 + 3 * (-1) + 3 * (-1) = -10 < 0. Its output stays at -1.
Hopfield networks
Now the bottom-left neuron.
The same: 3 * 1 + (-1) * (-1) = 4 > 0, the output stays at +1.
Hopfield networks
But the bottom-middle neuron has to flip its sign: -1 * 1 + 4 * 1 + 3 * (-1) - 1 * (-1) = 1 > 0.
Its new output is +1.
Hopfield networks
We can continue evaluating the neurons, but nobody will flip its sign.
This configuration is a stable pattern of the network.
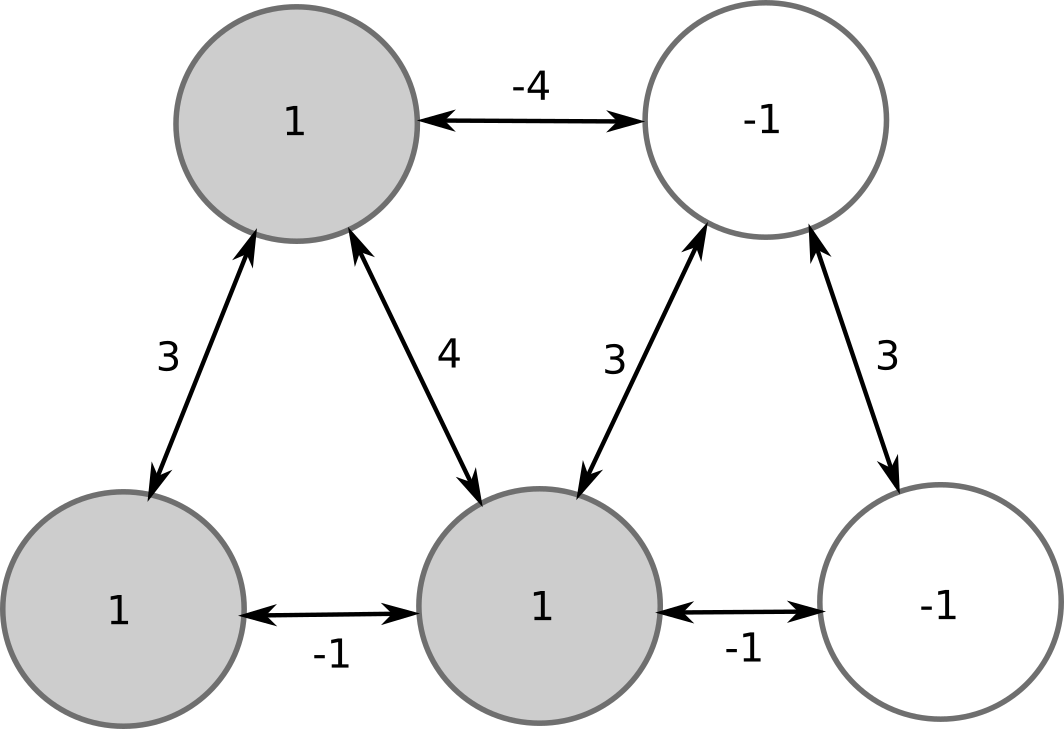
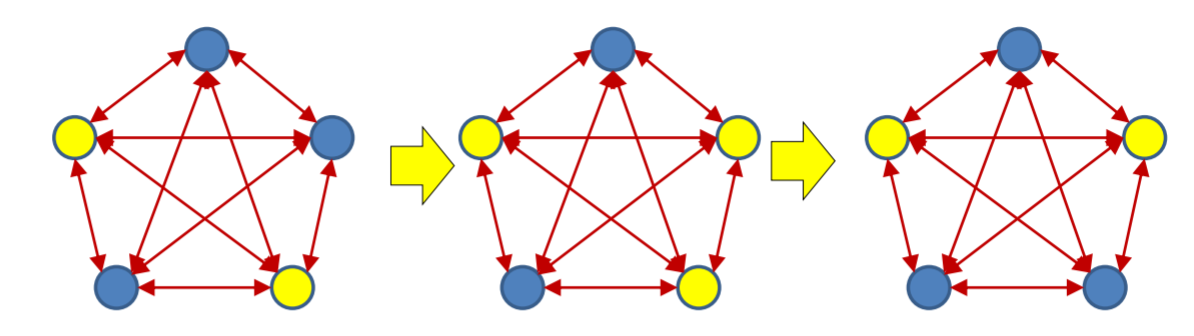
Hopfield networks
There is another stable pattern, where the two other neurons are active: symmetric or ghost pattern.
All other patterns are unstable and will eventually lead to one of the two stored patterns.
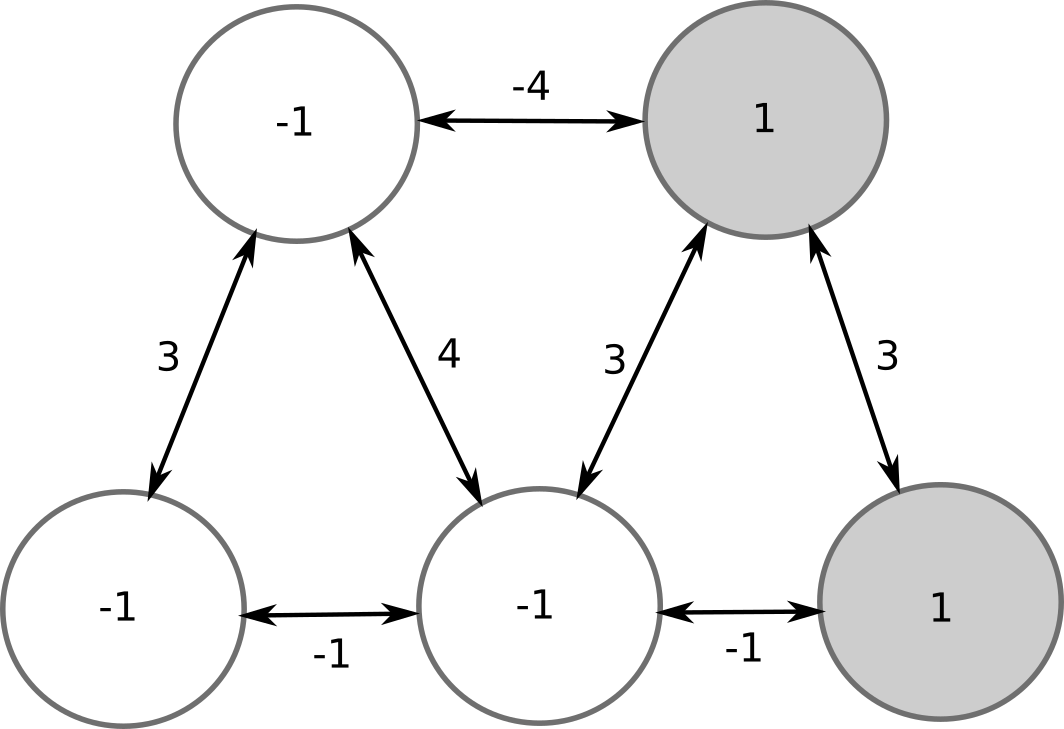
Hopfield networks
The weight matrix W allows to encode a given number of stable patterns, which are fixed points of the network’s dynamics.
Any initial configuration will converge to one of the stable patterns.
Hopfield networks
Initialize a symmetrical weight matrix without self-connections.
Set an input to the network through the bias \mathbf{b}.
while not stable:
Pick a neuron i randomly.
Compute its potential:
x_i = \sum_{j \neq i} w_{ji} \, y_j + b
- Flip its output if needed:
y_i = \text{sign}(x_i)
Asynchronous evaluation
Why do we need to update neurons one by one, instead of all together as in ANNs (vector-based)?
Consider the two neurons below:
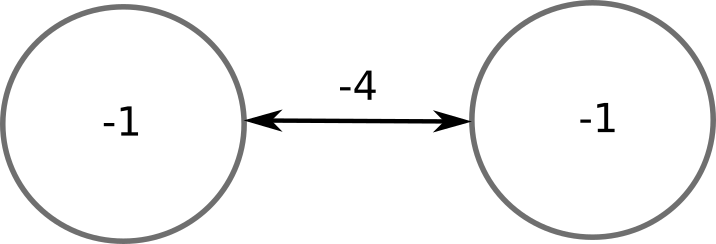
- If you update them at the same time, they will both flip:
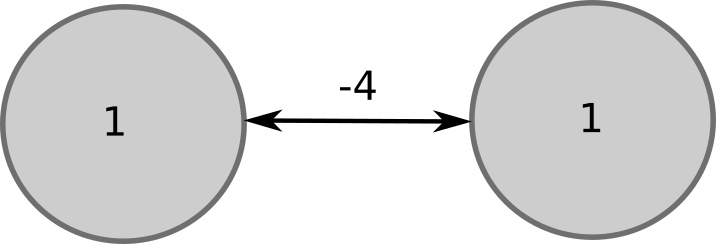
- But at the next update, they will both flip again: the network will oscillate for ever.
Asynchronous evaluation
- By updating neurons one at a time (randomly), you make sure that the network converges to a stable pattern:
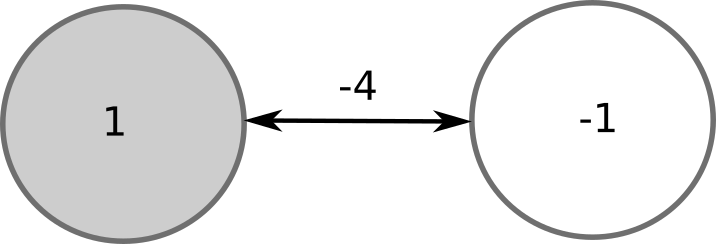
Energy of the Hopfield network
- The energy of the network can only decrease but has a lower bound.
E(\mathbf{y}) = -\frac{1}{2} \, \mathbf{y}^T \times W \times \mathbf{y} - \mathbf{b}^T \times \mathbf{y}
- Stable patterns are local minima of the energy function: no update can increase the energy.
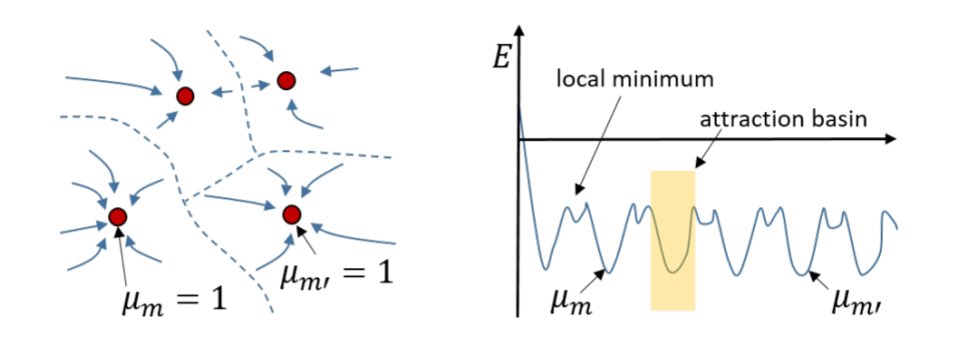
Energy of the Hopfield network
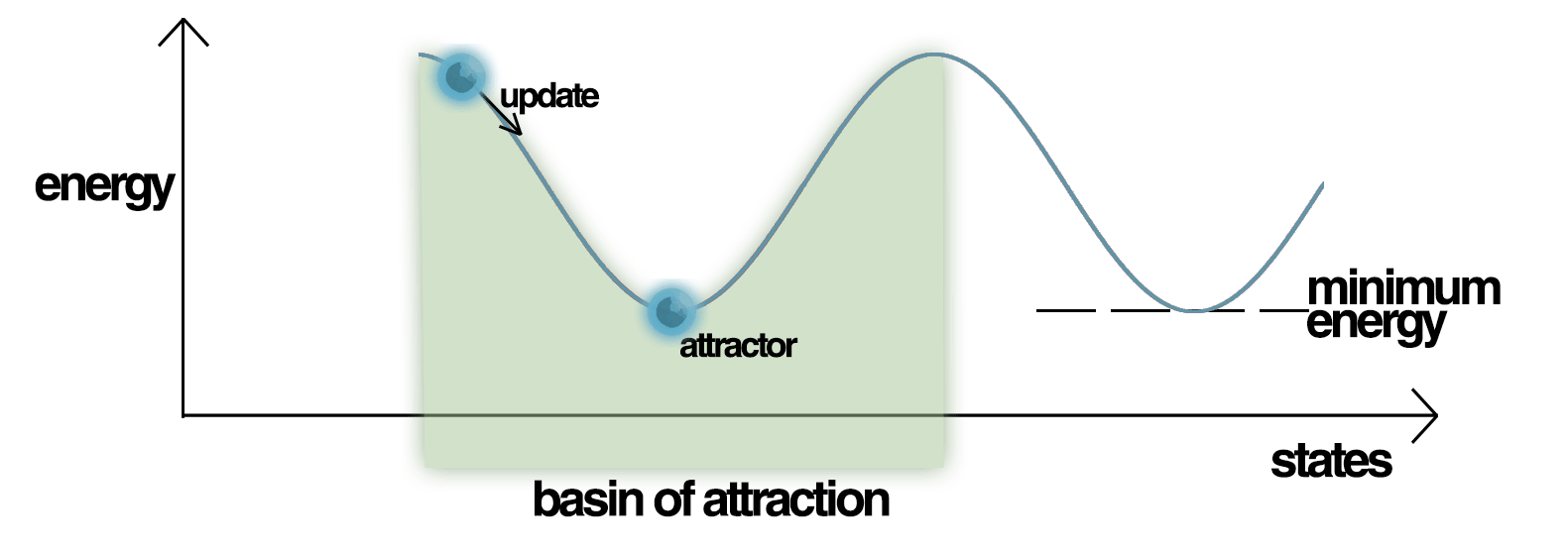
Stable patterns are point attractors.
Other patterns have higher energies and are attracted by the closest stable pattern (attraction basin).
Capacity of a Hopfield network
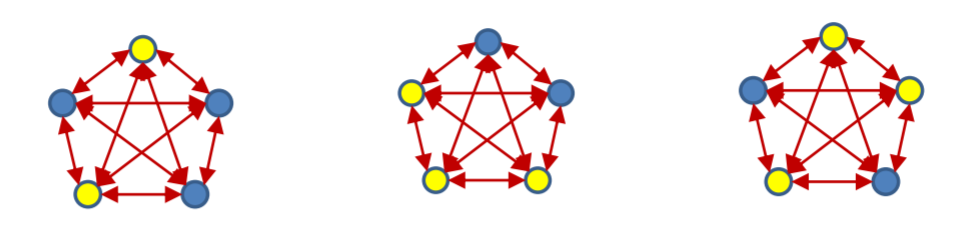
- It can be shown that for a network with N units, one can store up to 0.14 N different patterns:
C \approx 0.14 \, N
If you have 1000 neurons, you can store 140 patterns.
As you need 1 million weights for it, it is not very efficient…
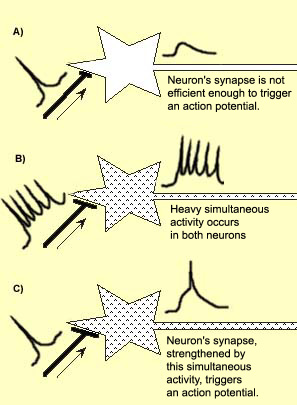
Hebb’s rule: Cells that fire together wire together
When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.
Donald Hebb, 1949
Spurious patterns
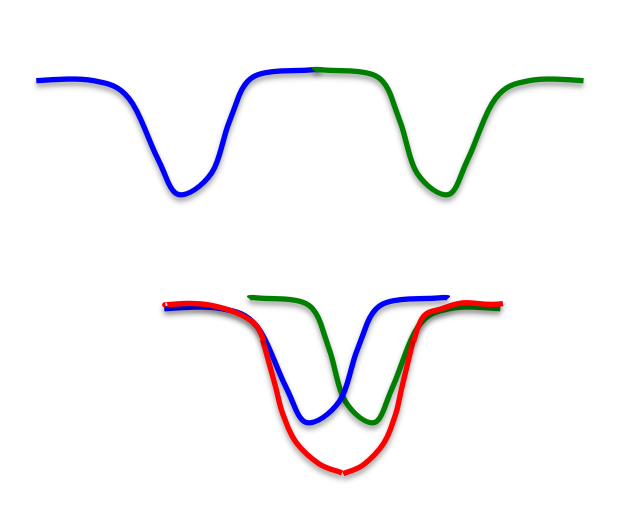
The problem when the capacity of the network is full is that the stored patterns will start to overlap.
The retrieved patterns will be a linear combination of the stored patterns, what is called a spurious pattern or metastable state.
\mathbf{y} = \pm \, \text{sign}(\alpha_1 \, \mathbf{y}^1 + \alpha_2 \, \mathbf{y}^2 + \dots + \alpha_P \, \mathbf{y}^P)
- A spurious pattern has never seen by the network, but is remembered like other memories (hallucinations).
Unlearning methods (Hopfield, Feinstein and Palmer, 1983) use a sleep / wake cycle:
When the network is awake, it remembers patterns.
When the network sleeps (dreams), it unlearns spurious patterns.
Applications of Hopfield networks
Optimization:
Traveling salesman problem http://fuzzy.cs.ovgu.de/ci/nn/v07_hopfield_en.pdf
Timetable scheduling
Routing in communication networks
Physics:
- Spin glasses (magnetism)
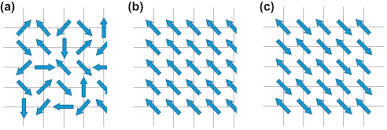
Computer Vision:
- Image reconstruction and restoration
Neuroscience:
- Models of the hippocampus, episodic memory
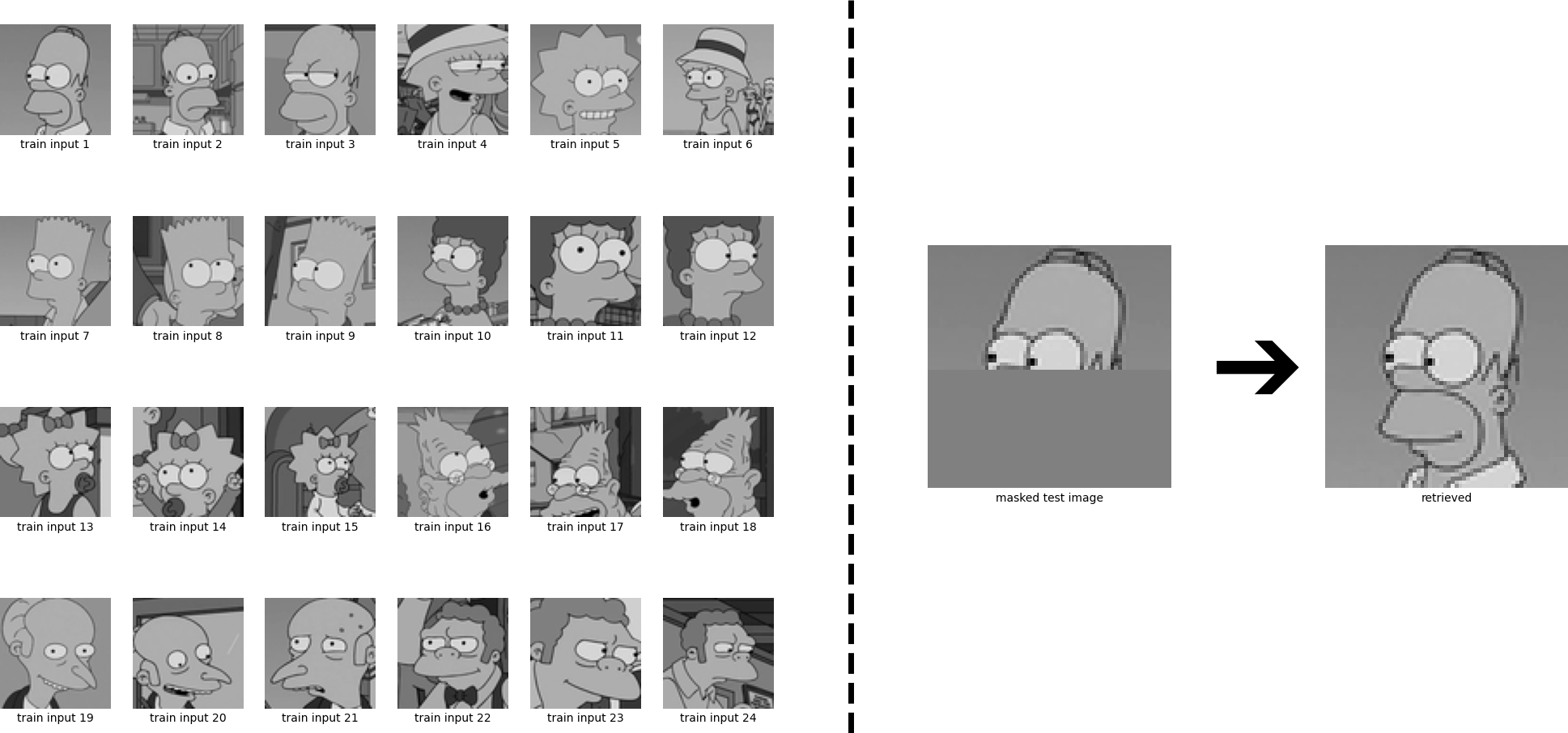
Problem with old-school Hopfield networks
The problems with Hopfield networks are:
Their limited capacity 0.14 \, N.
Ghost patterns (reversed images).
Spurious patterns (bad separation of patterns).
Retrieval is not error-free.
In this example, the masked Homer is closer to the Bart pattern in the energy function, so it converges to its ghost pattern.
Problem with old-school Hopfield networks
- The problem comes mainly from the fact the energy function is a quadratic function of the dot product between a state \mathbf{y} and the patterns \mathbf{y}^k:
E(\mathbf{y}) \approx -\frac{1}{2 P} \, \sum_{k=1}^P ((\mathbf{y}^k)^T \times \mathbf{y})^2
-((\mathbf{y}^k)^T \times \mathbf{y})^2 has minimum when \mathbf{y} = \mathbf{y}^k.
Quadratic functions are very wide, so it is hard to avoid overlap between the patterns.
- If we had a sharper energy functions, could not we store more patterns and avoid interference?
Modern Hopfield networks
The increased capacity of the modern Hopfield network makes sure that you store many patterns without interference (separability of patterns).
Convergence occurs in only one step (one update per neuron).
4 - Hopfield networks is all you need
Hopfield networks is all you need
- The update rule that minimizes the energy
E(\mathbf{y}) = - \text{lse}(\beta, X^T \, \mathbf{y}) + \frac{1}{2} \, \mathbf{y}^T \mathbf{y} + \beta^{-1} \, \log P + \frac{1}{2} \, M
is:
\mathbf{y} = \text{softmax}(\beta \, \mathbf{y} \, X^T) \, X^T
Why? Just read the 100 pages of mathematical proof.
Take home message: these are just matrix-vector multiplications and a softmax. We can do that!
Hopfield networks is all you need
- Continuous Hopfield networks can retrieve precisely continous vectors with an exponential capacity.
Hopfield networks is all you need
The sharpness of the attractors is controlled by the temperature parameter \beta.
You decide whether you want single patterns or meta-stable states, i.e. combinations of similar patterns.
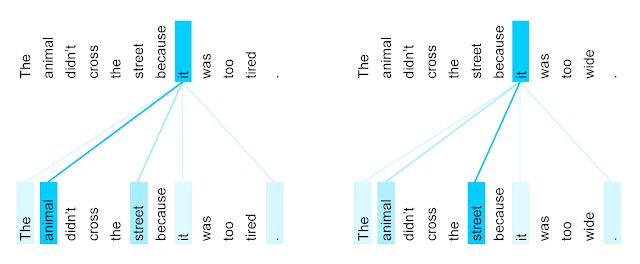
Why would we want that? Because it is the principle of self-attention.
Which other words in the sentence are related to the current word?
Hopfield networks is all you need
- Using the representation of a word \mathbf{y}, as well as the rest of the sentence X, we can retrieve a new representation \mathbf{y}^\text{new} that is a mixture of all words in the sentence.
\mathbf{y}^\text{new} = \text{softmax}(\beta \, \mathbf{y} \, X^T) \, X^T
This makes the representation of a word more context-related.
The representations \mathbf{y} and X can be learned using weight matrices, so backpropagation can be used.
This was the key insight of the transformer network that has replaced attentional RNNs in NLP.
Hopfield layers can replace the transformer self-attention with a better performance.
The transformer network was introduced with the title “Attention is all you need”, hence the title of this paper…
The authors claim that a Hopfield layer can also replace fully-connected layers, LSTM layers, attentional layers, but also SVM, KNN or LVQ…
