Neurocomputing
Reservoir computing
Professur für Künstliche Intelligenz - Fakultät für Informatik
Reservoir computing
The concept of Reservoir Computing (RC) was developed simultaneously by two researchers at the beginning of the 2000s.
Herbert Jaeger (Bremen) introduced echo-state networks (ESN) using rate-coded neurons (Jaeger, 2001).
Wolfgang Maass (TU Graz) introduced liquid state machines (LSM) using spiking neurons (Maass et al., 2002).
What is wrong with RNNs and LSTMs?
The recurrent networks from ML (LSTM, GRU) are very powerful thanks to the backpropagation through time (BPTT) algorithm.
However, they suffer from several problems:
- Long training times (multiple BP operations per step -> we have to limit the horizon)
- Vanishing gradients -> not-so-long-term dependencies
- Need for precisely sampled inputs (no sparse data)
- Robustness to noise and outliers.
1 - Echo-state networks
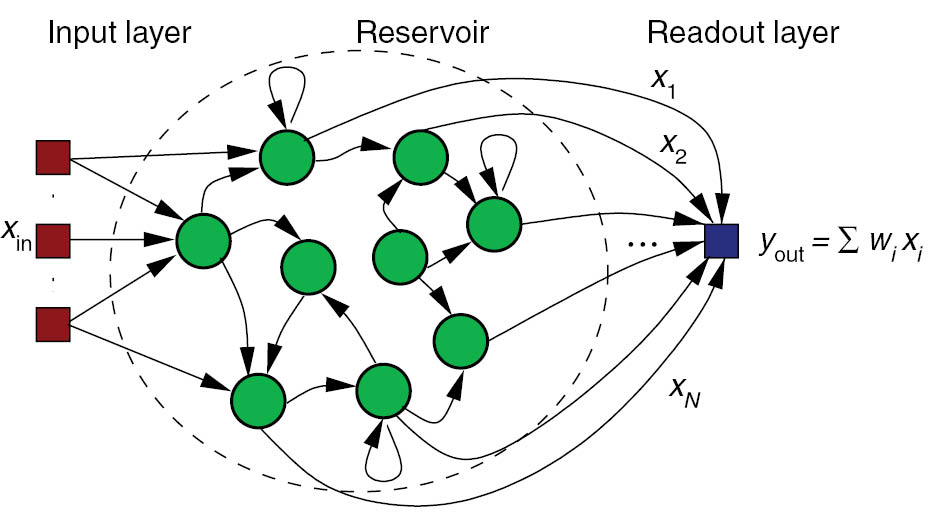
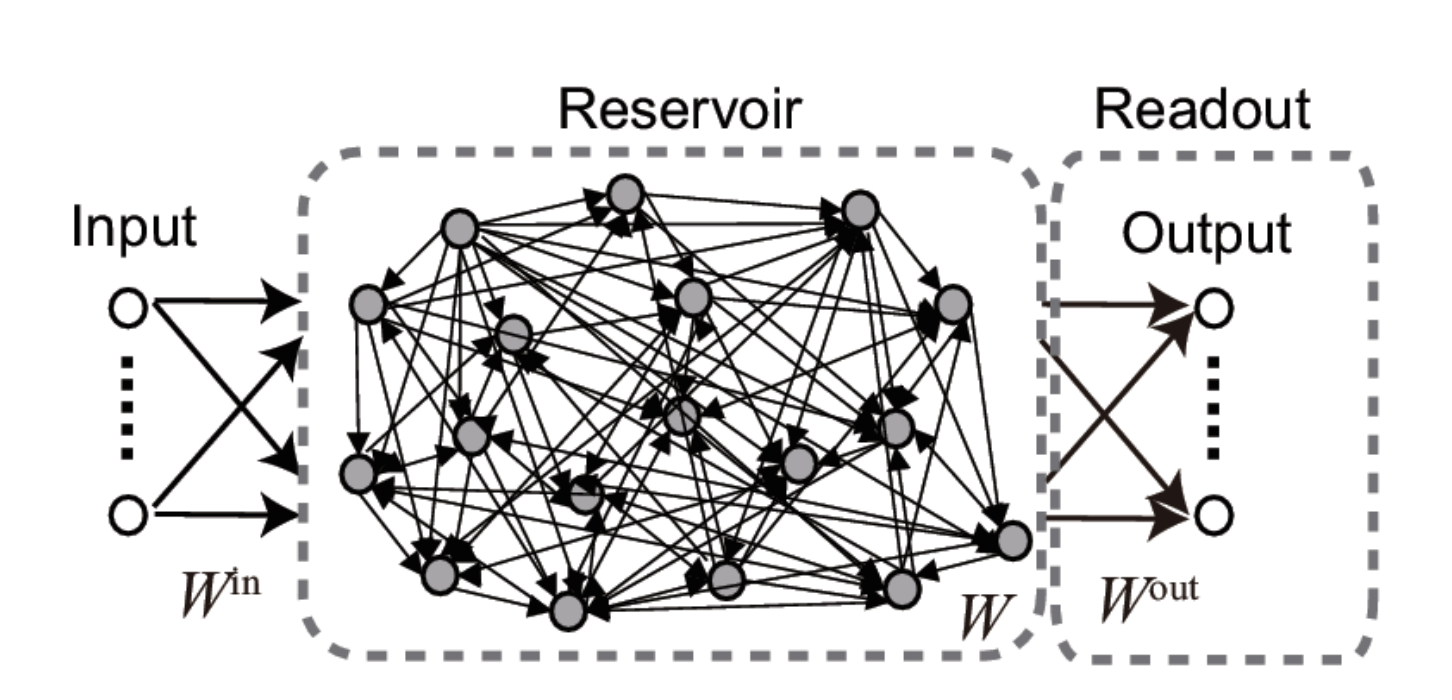
Echo-state networks
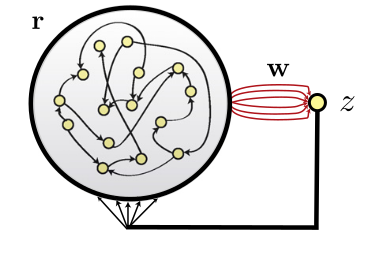
- An ESN is a set of recurrent units (sparsely connected) exhibiting complex spatiotemporal dynamics.
Rate-coded neurons in the reservoir integrate inputs and recurrent connections using an ODE: \tau \, \frac{d \mathbf{x}(t)}{dt} + \mathbf{x}(t) = W^\text{IN} \times \mathbf{I}(t) + W \times \mathbf{r}(t)
The output of a neuron typically uses the
tanhfunction (between -1 and 1):
\mathbf{r}(t) = \tanh \, \mathbf{x}(t)
- Readout neurons (or output neurons) transform linearly the activity in the reservoir:
\mathbf{z}(t) = W^\text{OUT} \times \mathbf{r}(t)
In the classical version of the ESN, only the readout weights are learned, not the recurrent ones.
One can use supervised learning to train the readout neurons to reproduce desired targets.
Tanaka et al. (2019) Recent advances in physical reservoir computing: A review. Neural Networks 115, 100–123.
Echo-state networks
Inputs \mathbf{I}(t) bring the recurrent units in a given state or trajectory.
The recurrent connections inside the reservoir create different dynamics \mathbf{r}(t) depending on the strength of the weight matrix.
Readout neurons linearly transform the recurrent dynamics into temporal outputs \mathbf{z}(t).
Supervised learning (delta learning rule, OLS) trains the readout weights to reproduce a target \mathbf{t}(t).
It is similar to a MLP with one hidden layer, but the hidden layer has dynamics.

Scaling factor
Reservoirs only need a few hundreds of units in the reservoir to learn complex functions (e.g. N=200).
The recurrent weights are initialized randomly using a normal distribution with mean 0 and deviation \frac{g}{\sqrt{N}}:
w_{ij} \sim \mathcal{N}(0, \frac{g}{\sqrt{N}})
g is a scaling factor characterizing the strength of the recurrent connections, what leads to different dynamics.
g is linked to the spectral radius of the recurrent weight matrix (highest eigenvalue).
The recurrent weight matrix is often sparse:
A subset of the possible connections N \times N has non-zero weights.
Typically, only 10% of the possible connections are created.
Depending on the value of g, the dynamics of the reservoir can exhibit different stable or cyclic attractors.
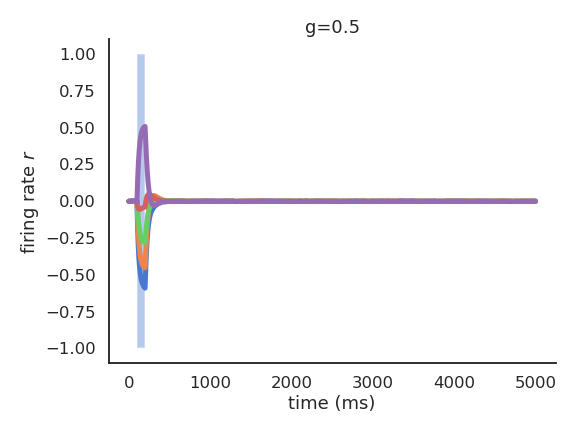
Let’s have a look at the activity of a few neurons after the presentation of a short input.
Echo-state networks
- When g<1, the network has no dynamics: the activity quickly fades to 0 when the input is removed.
Echo-state networks
- For g=1, the reservoir exhibits some transcient dynamics but eventually fades to 0 (echo-state property).
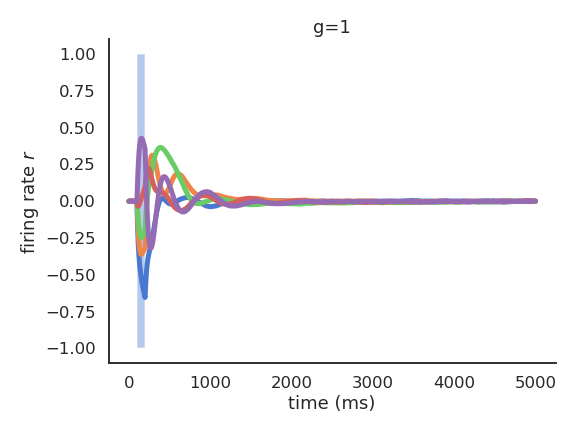
Echo-state networks
- For 1 \leq g \leq 1.5, the reservoir can exhibit many stable attractors due to its rich dynamics.
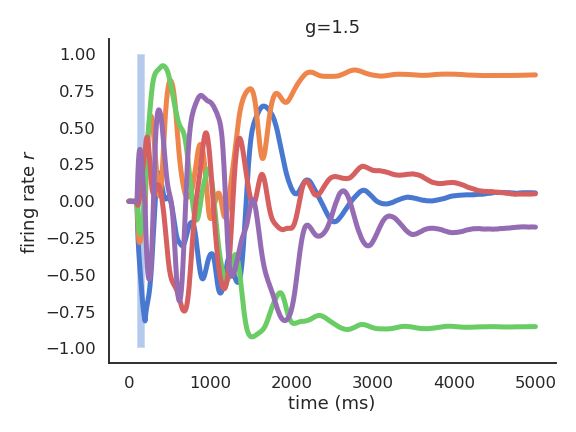
Echo-state networks
- For higher values of g, there are no stable attractors anymore: chaotic behavior.
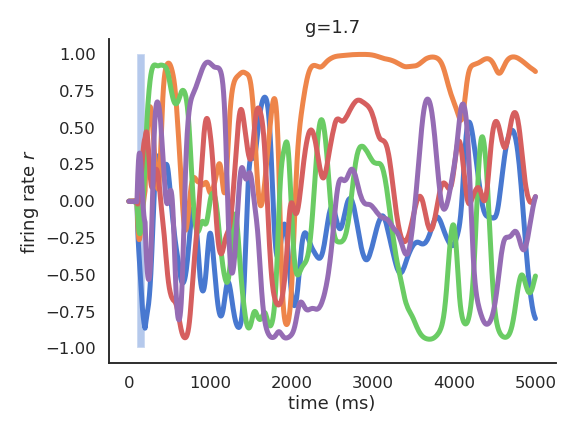
Representational power at the edge of chaos
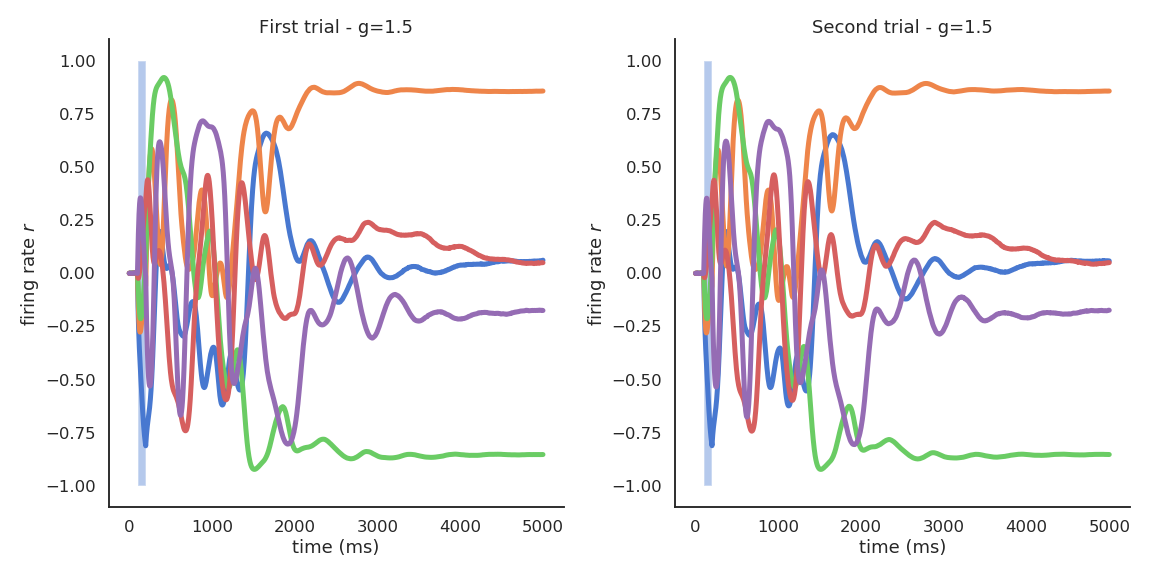
- For g = 1.5, different inputs (initial states) lead to different attractors.
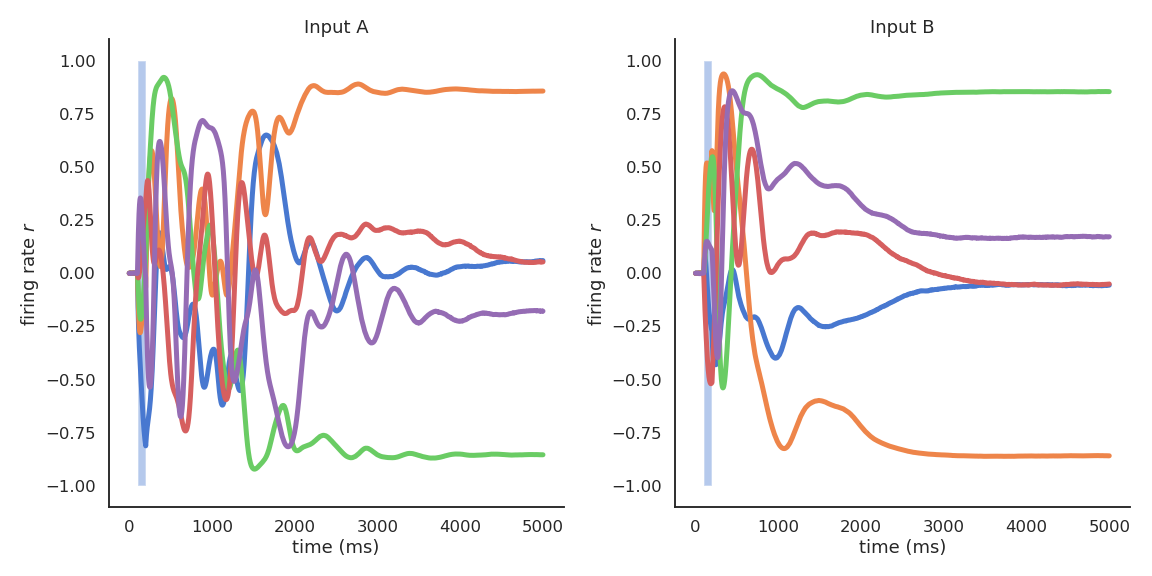
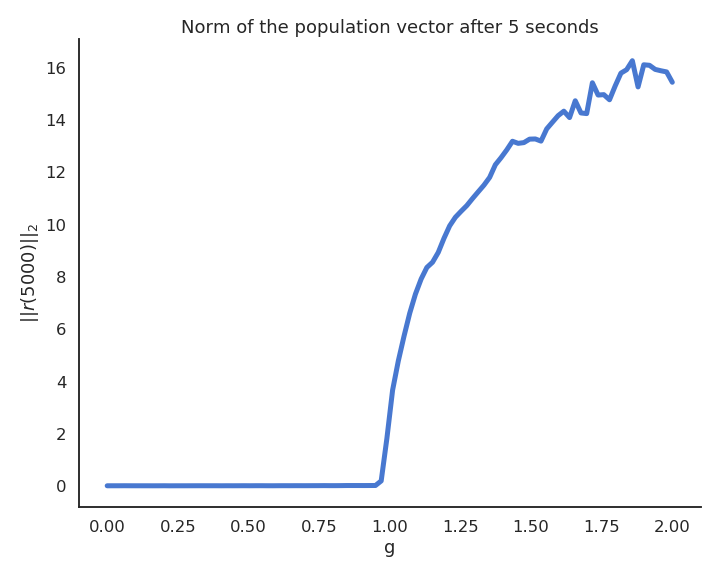
Apparition of stable attractors
- The weight matrix must have a scaling factor above 1 to exhibit non-zero attractors.
Stable attractors at the edge of chaos
- For a single input, the attractor is always the same, even in the presence of noise or perturbations.
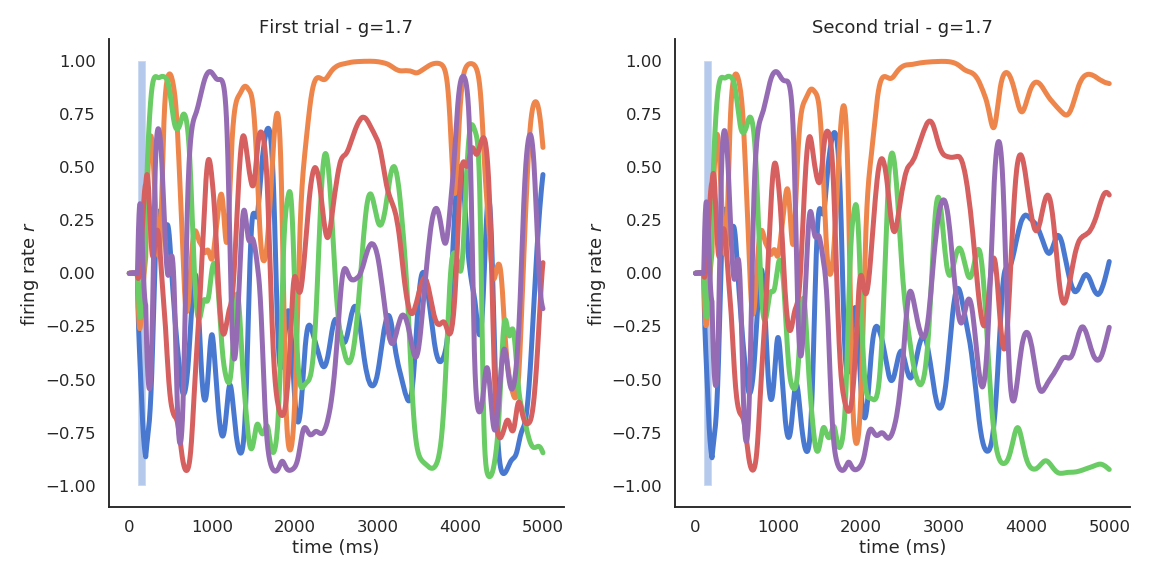
Chaotic behavior for high values of g
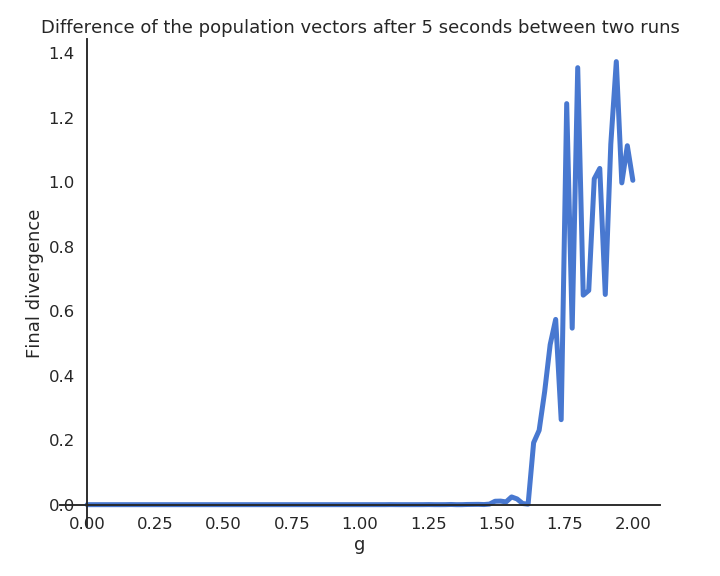
- In the chaotic regime, the slightest uncertainty on the initial conditions (or the presence of noise) produces very different trajectories on the long-term.
Edge of chaos
The chaotic regime appears for g > 1.5.
g=1.5 is the edge of chaos: the dynamics are very rich, but the network is not chaotic yet.
Lorenz attractor
The Lorenz attractor is a famous example of a chaotic attractor.
The position x, y, z of a particle is describe by a set of 3 deterministic ordinary differential equations:
\begin{cases} \dfrac{dx}{dt} = \sigma \, (y - x) \\ \\ \dfrac{dy}{dt} = x \, (\rho - z) - y \\ \\ \dfrac{dz}{dt} = x\, y - \beta \, z \\ \end{cases}
- The resulting trajectories over time have complex dynamics and are chaotic: the slightest change in the initial conditions generates different trajectories.
Training the readout neurons

- Using the reservoir as input, the linear readout neurons can be trained to reproduce any non-linear target signal over time:
\mathbf{z}(t) = W^\text{OUT} \times \mathbf{r}(t)
- The batch ordinary least squares (OLS) regression algorithm using the matrix \mathbf{R} of recorded activations is often used:
W^\text{OUT} = (\mathbf{R}^T \times \mathbf{R})^{-1} \times \mathbf{R}^T \times \mathbf{T}
- Reservoirs are universal approximators:
Given enough neurons in the reservoir and dynamics at the edge of the chaos, a RC network can approximate any non-linear function between an input signal \mathbf{I}(t) and a target signal \mathbf{t}(t).
Pattern separation
The reservoir projects a low-dimensional input into a high-dimensional spatio-temporal feature space where trajectories becomes linearly separable.
The reservoir increases the distance between the input patterns.
Input patterns are separated in both space (neurons) and time: the readout neurons need much less weights than the equivalent MLP: better generalization and faster learning.
The only drawback is that it does not deal very well with high-dimensional inputs (images).
Seoane (2019) Evolutionary aspects of reservoir computing. Philosophical Transactions of the Royal Society B.
Applications of Reservoir Computing
See Zhang and Vargas (2023).
Applications of Reservoir Computing
- Forecasting: ESN are able to predict the future of chaotic systems (stock market, weather) much better than static NN.
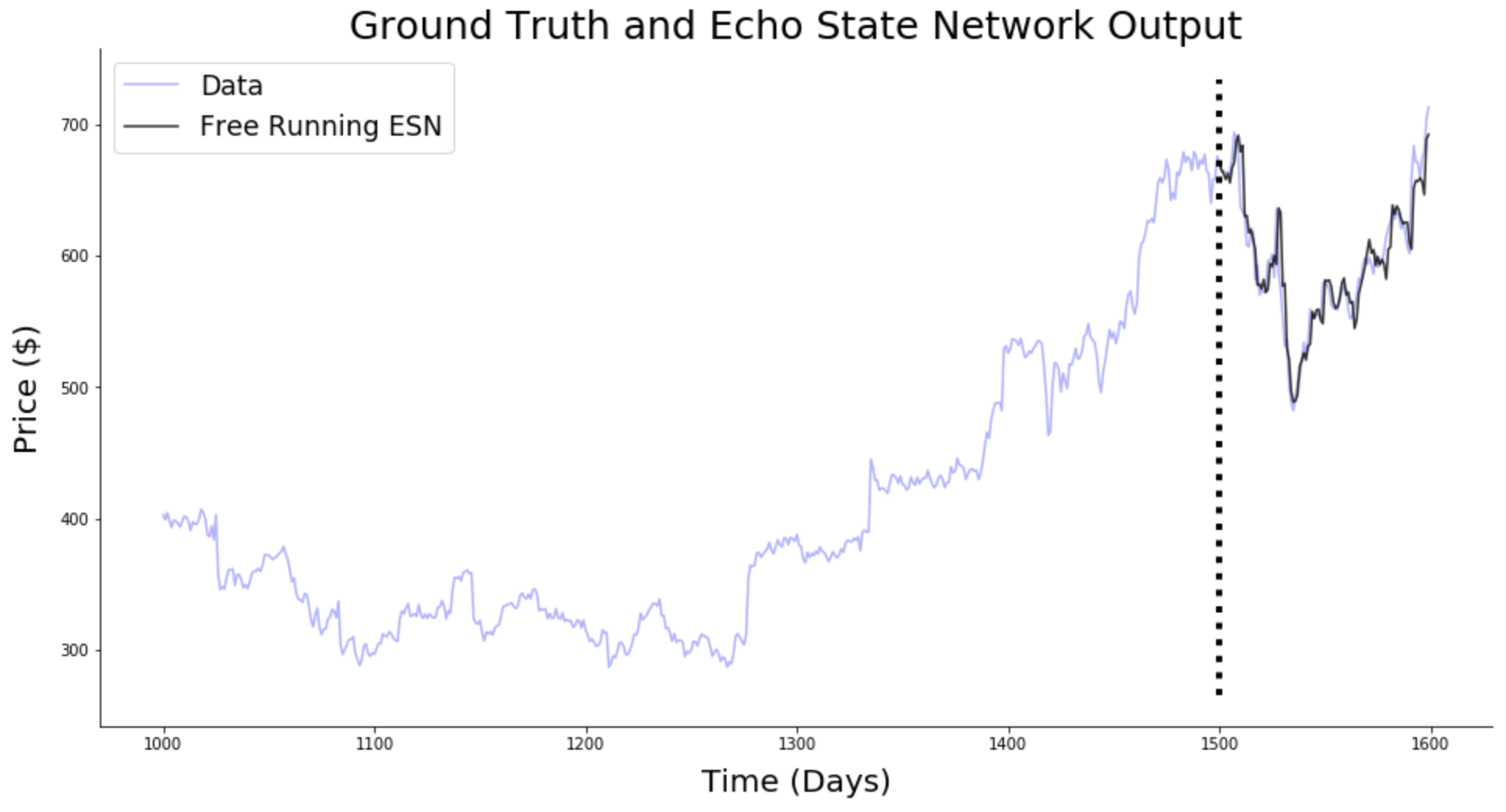
Applications of Reservoir Computing
- Physics: RC networks can be used to predict the evolution of chaotic systems (Lorenz, Mackey-Glass, Kuramoto-Sivashinsky) at very long time scales (8 times the Lyapunov time).

Pathak et al. (2018) Model-Free Prediction of Large Spatiotemporally Chaotic Systems from Data: A Reservoir Computing Approach. Physical Review Letters 120, 024102–024102.
Applications of Reservoir Computing
NLP: RC networks can grasp the dynamics of language, i.e. its grammar.
RC networks can be trained to produce predicates (“hit(Mary, John)”) from sentences (“Mary hit John” or “John was hit by Mary”)
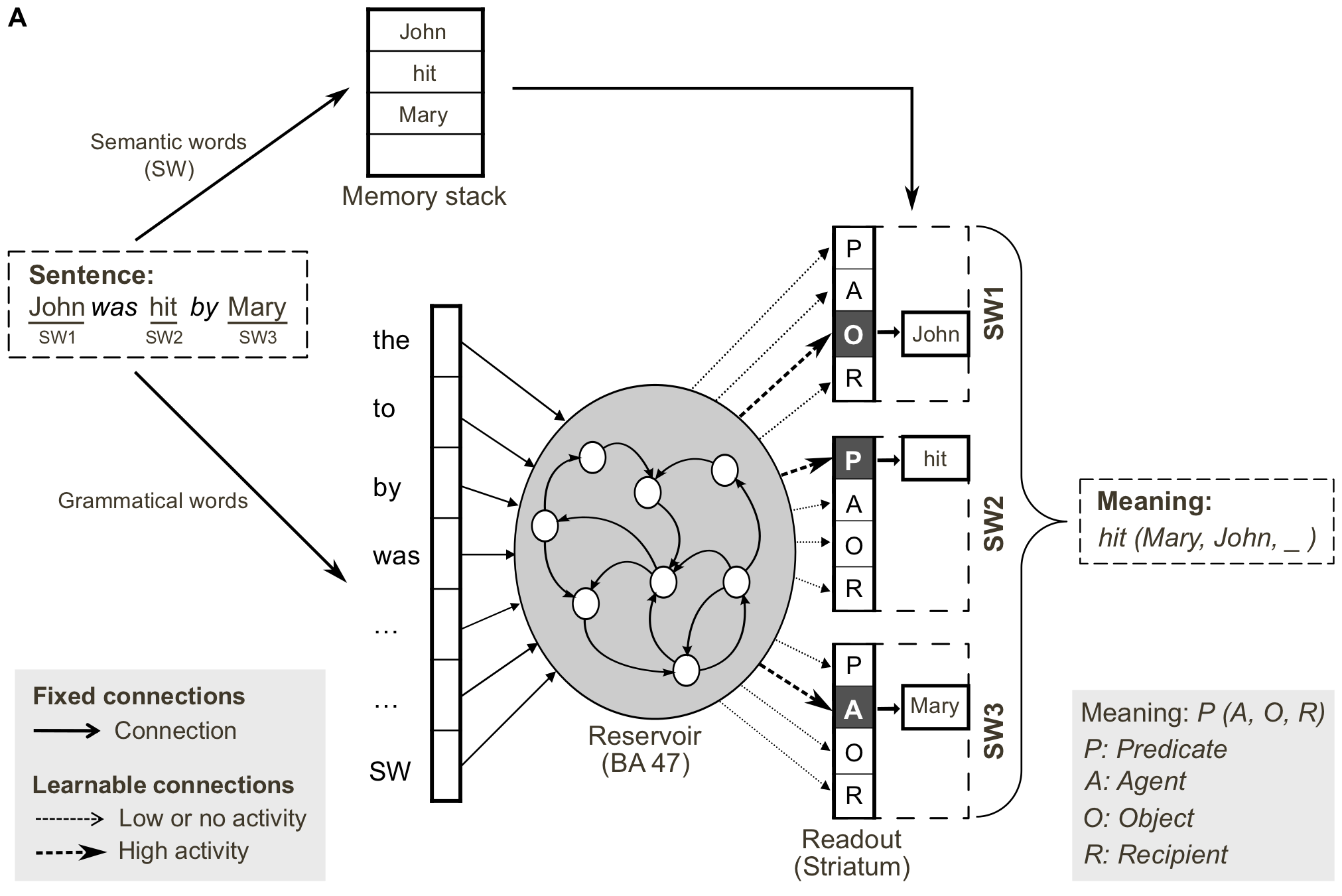
Hinaut and Dominey (2013) Real-Time Parallel Processing of Grammatical Structure in the Fronto-Striatal System. PLOS ONE 8, e52946.
Application of Reservoir Computing
Physical Reservoir Computing
The cool thing with reservoirs is that they do not have to be simulated by classical von Neumann architectures (CPU, GPU).
Anything able to exhibit dynamics at the edge of chaos can be used:
- VLSI (memristors), magnetronics, photonics (lasers), spintronics (nanoscale electronics)…
This can limit drastically the energy consumption of ML algorithms (200W for a GPU).
Even biological or physical systems can be used…
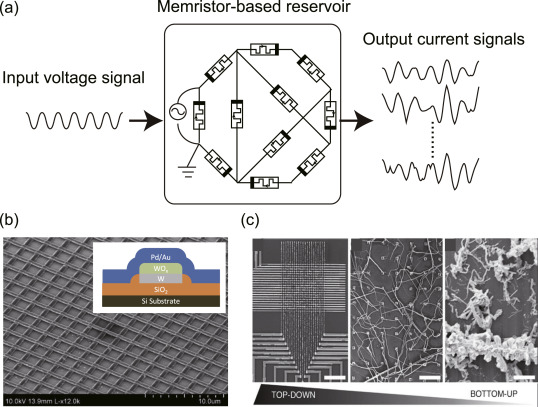
Tanaka et al. (2019) Recent Advances in Physical Reservoir Computing: A Review. arXiv:1808.04962
Pattern recognition in a bucket

A bucket of water can be used as a reservoir.
Different motors provide inputs to the reservoir by creating weights.
The surface of the bucket is recorded and used as an input to a linear algorithm.
It can learn non-linear operations (XOR) or even speech recognition.

Fernando and Sojakka (2003) Pattern Recognition in a Bucket. in Advances in Artificial Life Lecture Notes in Computer Science.
RC with a in-silico culture of biological neurons
- Real biological neurons can be kept alive in a culture and stimulated /recorded to implement a reservoir.
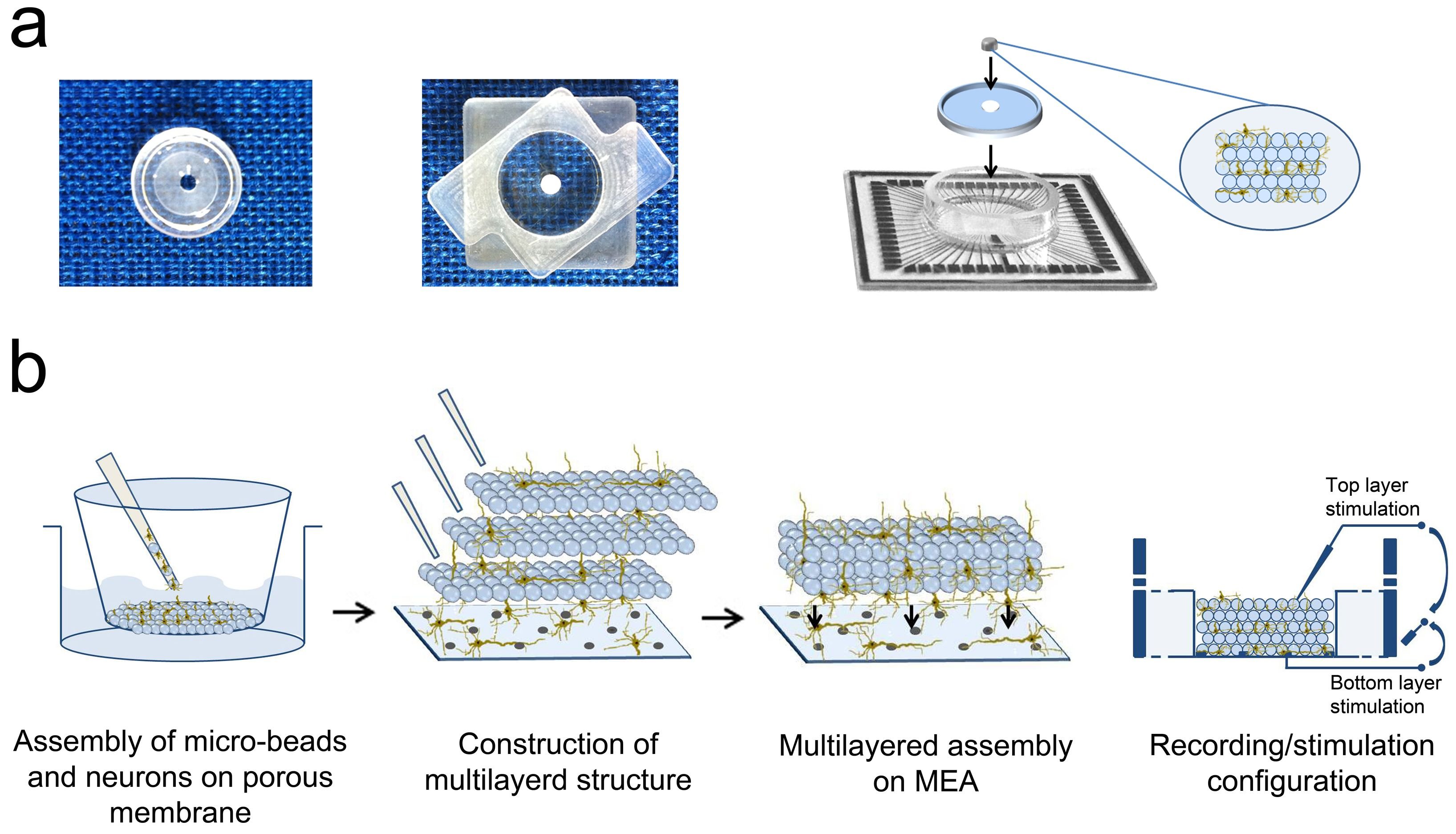
Frega et al. (2014) Network dynamics of 3D engineered neuronal cultures: a new experimental model for in-vitro electrophysiology. Scientific Reports 4, 1–14.
RC in cultures of E.Coli bacteria
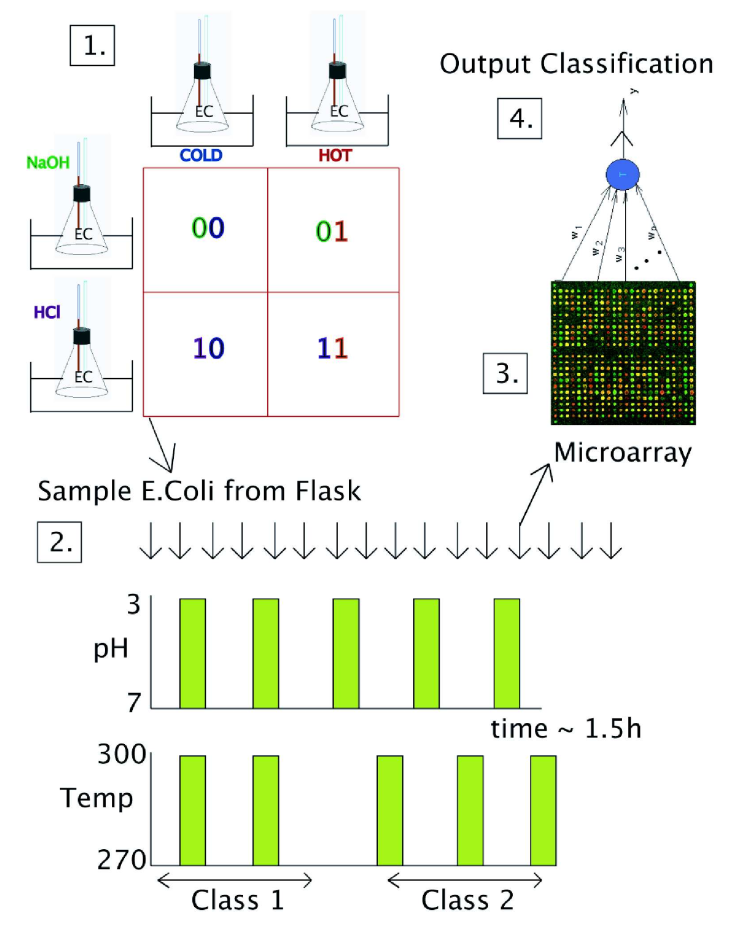
Escherichia Coli bacteria change their mRNA in response to various external factors (temperature, chemical products, etc) and interact with each other.
Their mRNA encode a dynamical trajectory reflecting the inputs.
By placing them on a microarray, one can linearly learn to perform non-linear operations on the inputs.
Jones et al. (2007) Is there a Liquid State Machine in the Bacterium Escherichia Coli? in 2007 IEEE Symposium on Artificial Life, 187–191.
2 - FORCE learning

Sussillo and Abbott (2009) Generating coherent patterns of activity from chaotic neural networks. Neuron, 63(4), 544–557.
Feedback connections
- The output of the readout neurons can be fed back into the reservoir to stabilize the trajectories:
\tau \, \dfrac{d \mathbf{x}(t)}{dt} + \mathbf{x}(t) = W^\text{IN} \times \mathbf{I}(t) + W^\text{REC} \times \mathbf{r}(t) + W^\text{FB} \times \mathbf{z}(t)
This makes the reservoir much more robust to perturbations, especially at the edge of chaos.
The trajectories are more stable (but still highly dynamical), making the job of the readout neurons easier.
Using feedback, there is even no need for an input I(t). The target value t(t) just needs to be used by the readout layer which should learn to minimize the difference.
A reservoir with feedback can perform autoregression, for example time series prediction.
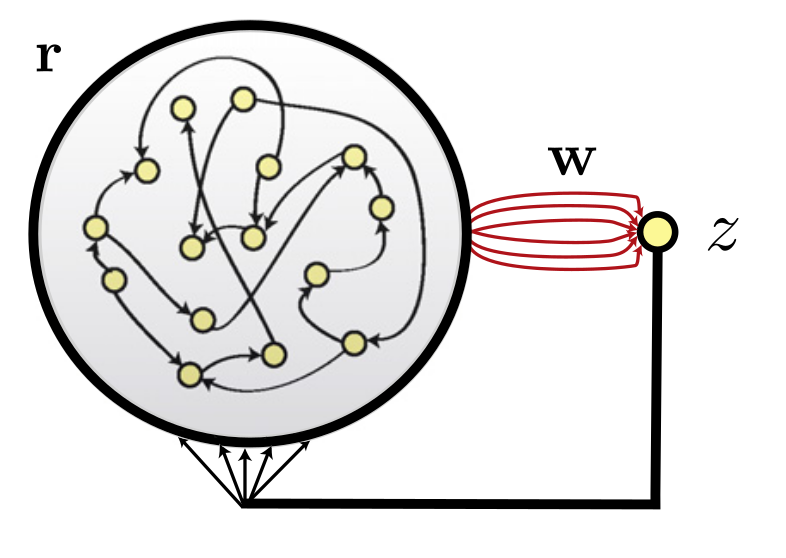
Sussillo and Abbott (2009) Generating coherent patterns of activity from chaotic neural networks. Neuron, 63(4), 544–557.
Online learning is not possible with simple regression rules
- However, using the feedback makes batch learning impossible, as the evolution of the reservoir’s activity depends on the readout:
\begin{cases} \tau \, \dfrac{d \mathbf{x}(t)}{dt} + \mathbf{x}(t) = W^\text{IN} \times \mathbf{I}(t) + W^\text{REC} \times \mathbf{r}(t) + W^\text{FB} \times \mathbf{z}(t) \\ \\ \mathbf{r}(t) = \tanh \, \mathbf{x}(t) \\ \\ \mathbf{z}(t) = W^\text{OUT} \times \mathbf{r}(t) \\ \end{cases}
- The batch ordinary least squares (OLS) regression algorithm makes the assumption that the samples over time t are i.i.d, which they clearly aren’t.
\mathcal{L}(W^\text{OUT}) = \mathbb{E}_t [||\mathbf{t}(t) - W^\text{OUT} \times \mathbf{r}(t)||^2]
W^\text{OUT} = (\mathbf{R}^T \times \mathbf{R})^{-1} \times \mathbf{R}^T \times \mathbf{T}
- Using the online delta-learning rule (batch size of 1) leads to catastrophic forgetting.
\Delta W^\text{OUT} = \eta \, (\mathbf{t}(t) - \mathbf{z}(t)) \times \mathbf{r}^T(t)
Recursive least squares (RLS)
If we wanted to take the temporal dependencies into account, we would need to apply BPTT to the recurrent weights: bad.
There exists a version of OLS which is online and allows to perform linear regression incrementally.
The math is complex, so here are some online resources if you are interested: here and there.
Let’s say we have already learned from the t-1 first samples, and get a new sample (\mathbf{z}(t), \mathbf{t}(t)).
How do we update the weights
The readout weights will be updated online using the error, the input and P:
\Delta W^\text{OUT} = \eta \, (\mathbf{t}_t - \mathbf{z}_t) \times P \times \mathbf{r}_t
where P is a running estimate of the inverse information matrix of the input :
P = (\mathbf{R}^T \times \mathbf{R})^{-1}
- This implements a form of adaptive learning rate: synapses where the uncertainty on the parameter estimates is high will learn faster than those which are certain.
Haykin (2002) Adaptive filter theory. Prentice Hall.
Recursive least squares (RLS)
- In practice, the inverse of the information matrix is updated at each time step t using the formula:
\Delta P = - \dfrac{(P \times \mathbf{r}_t) \times (P \times \mathbf{r}_t)^T}{1 + \mathbf{r}_t^T \times P \times \mathbf{r}_t}
and the weight updates are also normalized:
\Delta W^\text{OUT} = \eta \, (\mathbf{t}_t - \mathbf{z}_t) \times \dfrac{P}{1 + \mathbf{r}_t^T \times P \times \mathbf{r}_t} \times \mathbf{r}_t
Updating P requires n \times n operations per step, compared with the n operations needed by the delta learning rule, but at least it works…
This is the formula of a single readout neuron (\mathbf{t}_t and \mathbf{z}_t are actually scalars). If you have several output neurons, you need to update several P matrices…
FORCE Learning
FORCE learning (first-order reduced and controlled error) consists of feeding back the readout into the reservoir and using RLS.
FORCE learning allows to stabilize trajectories in the chaotic reservoir and generate complex patterns in an autoregressive manner.
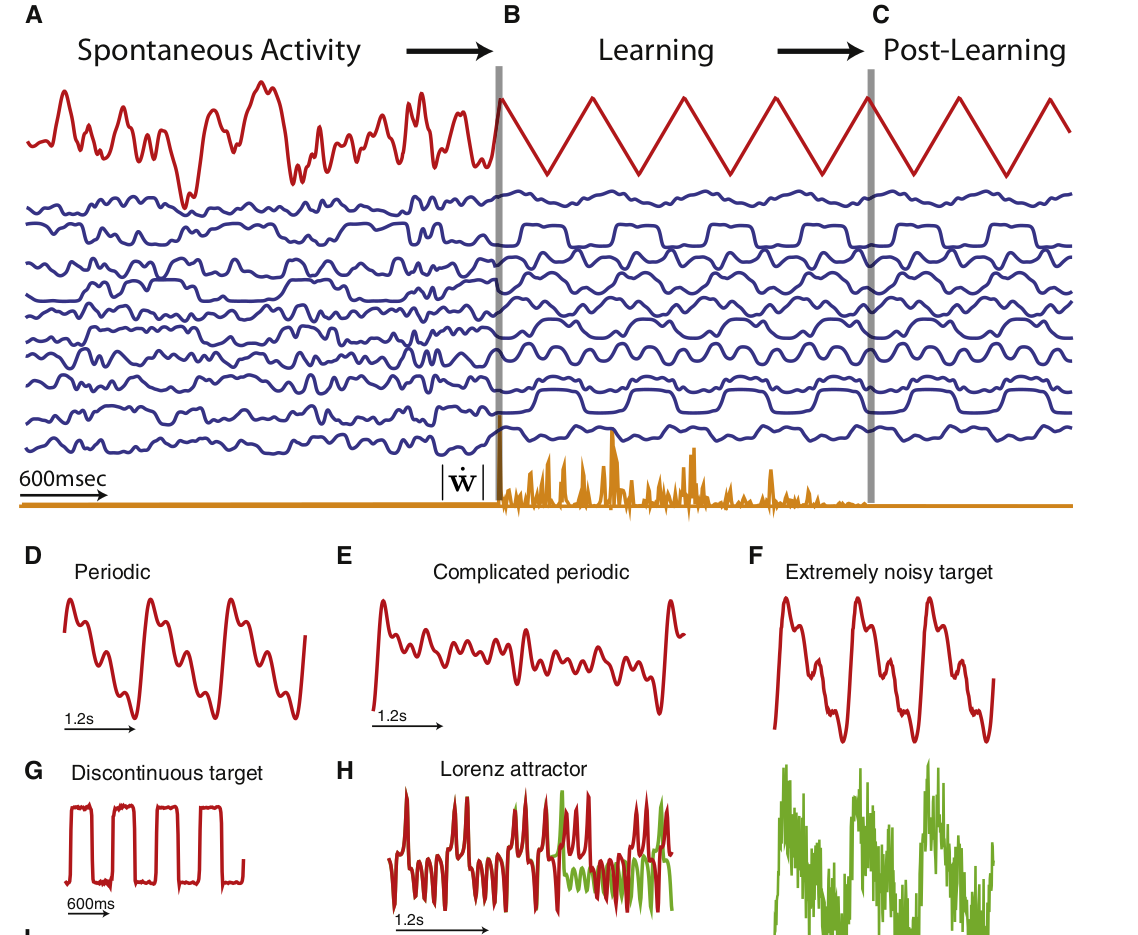
Sussillo and Abbott (2009) Generating coherent patterns of activity from chaotic neural networks. Neuron, 63(4), 544–557.
3 - Taming chaos by learning the recurrent weights

Laje and Buonomano (2013) Robust timing and motor patterns by taming chaos in recurrent neural networks. Nature Neuroscience, 16(7), 925–933.
Taming chaos by learning the recurrent weights
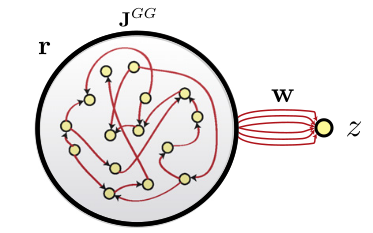
In classical RC networks, the recurrent weights are fixed and only the readout weights are trained.
The reservoir dynamics are fixed by the recurrent weights, we cannot change them.
Dynamics can be broken by external perturbations or high-amplitude noise.
The edge of chaos is sometimes too close.
If we could learn the recurrent weights, we could force the reservoir to have fixed and robust trajectories, while keeping interesting dynamics.
However, learning in a chaotic system, even with BPTT, is very hard.
Sussillo and Abbott (2009) Generating coherent patterns of activity from chaotic neural networks. Neuron, 63(4), 544–557. doi:10.1016/j.neuron.2009.07.018
Taming chaos by learning the recurrent weights

A classical network is trained to reproduce handwriting.
The two readout neurons produce a sequence of (x, y) positions for the pen.
It works quite well when the input is not perturbed.
If some perturbation enters the reservoir, the trajectory is lost.
Training the recurrent connections

We have an output error signal \mathbf{t}_t - \mathbf{z}_t at each time step.
Why can’t we just apply backpropagation (through time) on the recurrent weights?
\mathcal{L}(W, W^\text{OUT}) = \mathbb{E}_{t} [(\mathbf{t}_t - \mathbf{z}_t)^2]
- BPTT is too unstable: the slightest weight change impacts the whole dynamics.
FORCE Learning
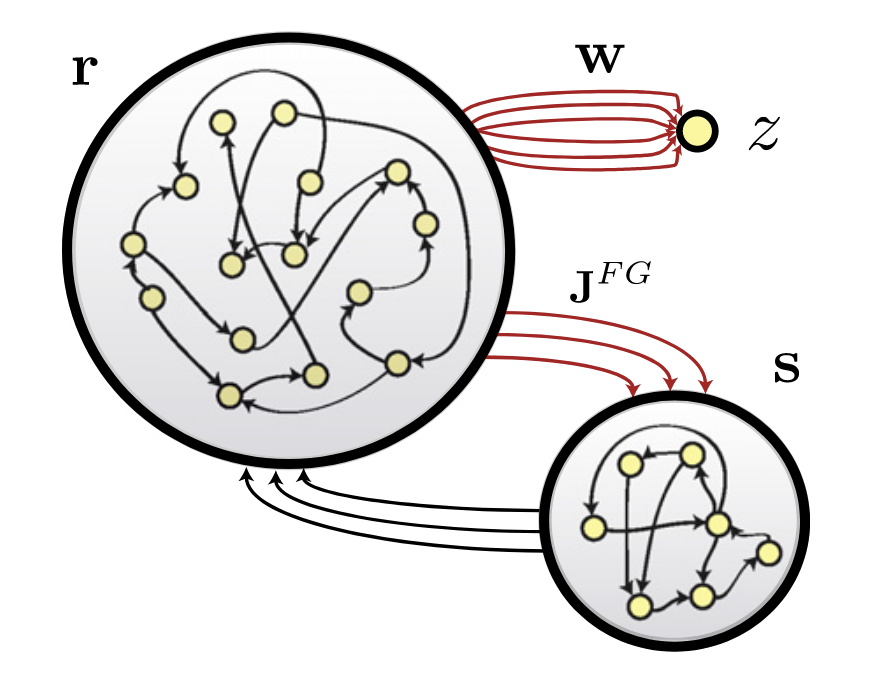
With FORCE learning, we have an error term for the readout weights.
For the recurrent weights, we would also need an error term.
It can computed by recording the dynamics during an initialization trial \mathbf{r}^*_t and forcing the recurrent weights to reproduce these dynamics in the learning trials:
\Delta W = - \eta \, (\mathbf{r}^*_t - \mathbf{r}_t) \times P \times \mathbf{r}_t
This is equivalent to having a fixed, external reservoir providing the targets.
See https://github.com/ReScience-Archives/Vitay-2016 for a reimplementation.
Sussillo and Abbott (2009) Generating coherent patterns of activity from chaotic neural networks. Neuron, 63(4), 544–557.
Taming Chaos in RC networks
- This allows to stabilize trajectories in the chaotic reservoir (taming chaos) and generate complex patterns.
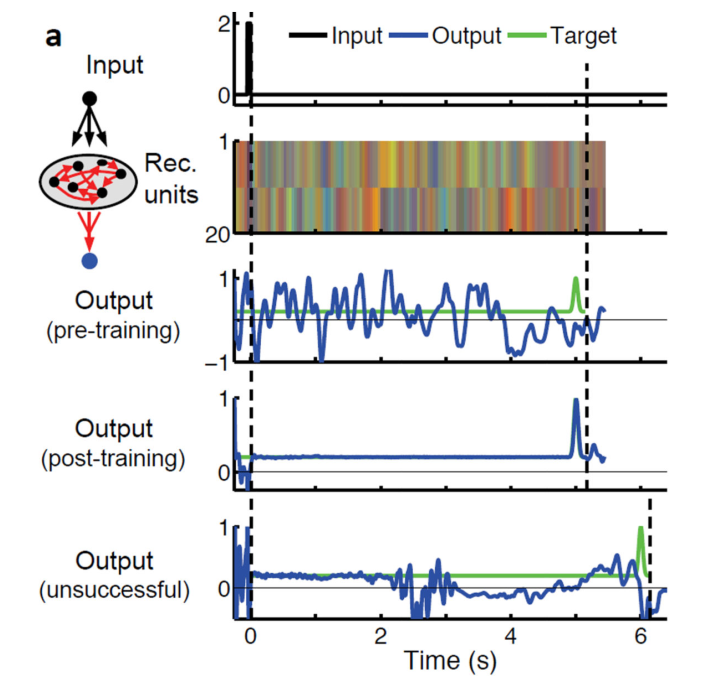
Laje and Buonomano (2013) Robust timing and motor patterns by taming chaos in recurrent neural networks. Nature Neuroscience, 16(7), 925–933.
Taming Chaos in RC networks
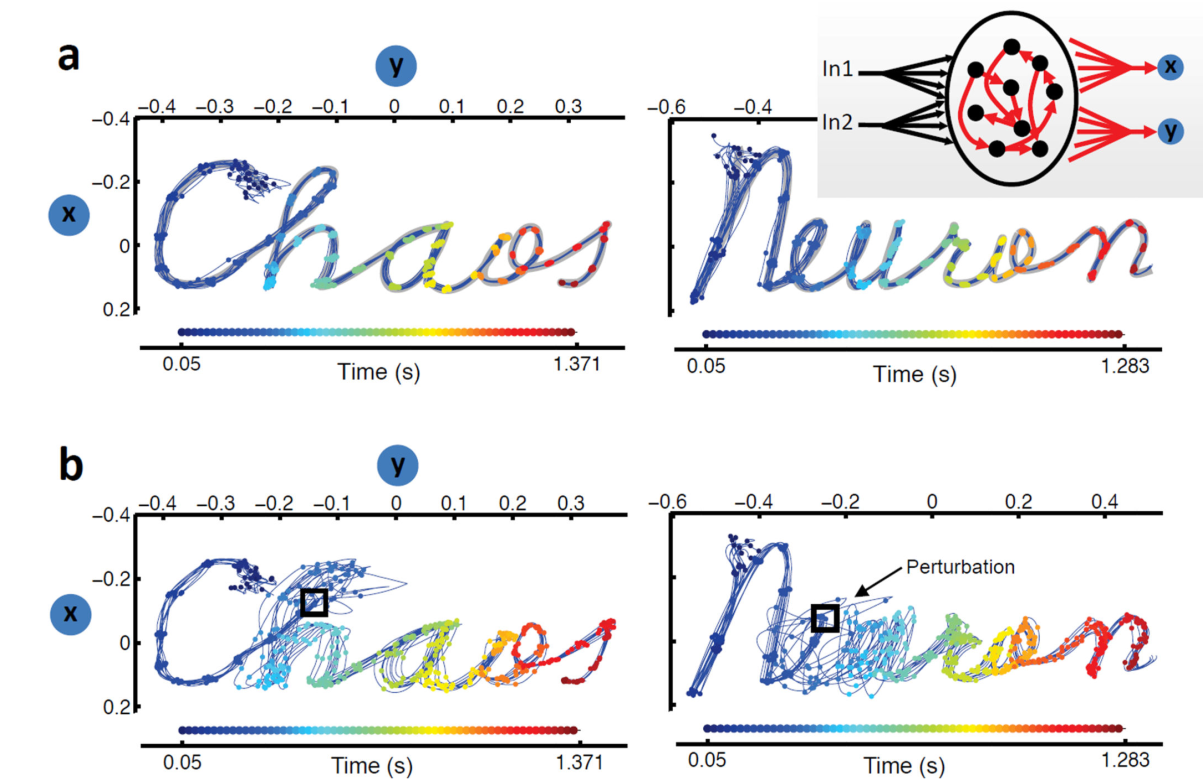
Laje and Buonomano (2013) Robust timing and motor patterns by taming chaos in recurrent neural networks. Nature Neuroscience, 16(7), 925–933.
4 - Biologically plausible reward modulated learning in RC

Miconi (2017) Biologically plausible learning in recurrent neural networks reproduces neural dynamics observed during cognitive tasks. eLife 6:e20899.
Biologically plausible reward modulated learning in RC
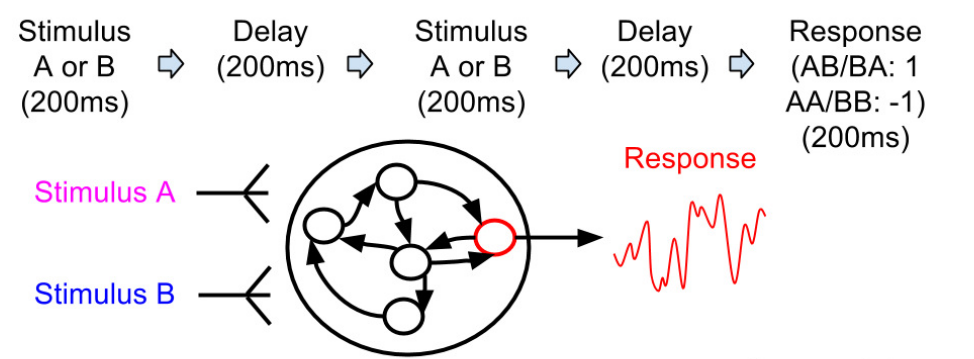
- Miconi proposed a realistic model of reward-based learning in a classical reservoir:
\tau \frac{d \mathbf{x}(t)}{dt} + \mathbf{x}(t) = W^\text{IN} \times \mathbf{I}(t) + W \times \mathbf{r}(t)
\mathbf{r}(t) = \tanh \mathbf{x}(t)
However, there are NO readout neurons: a random neuron of the reservoir is picked as output neuron.
Its activity at the end of a trial is used to provide a reward or not.
Miconi (2017) Biologically plausible learning in recurrent neural networks reproduces neural dynamics observed during cognitive tasks. eLife 6:e20899.
Biologically plausible reward modulated learning in RC
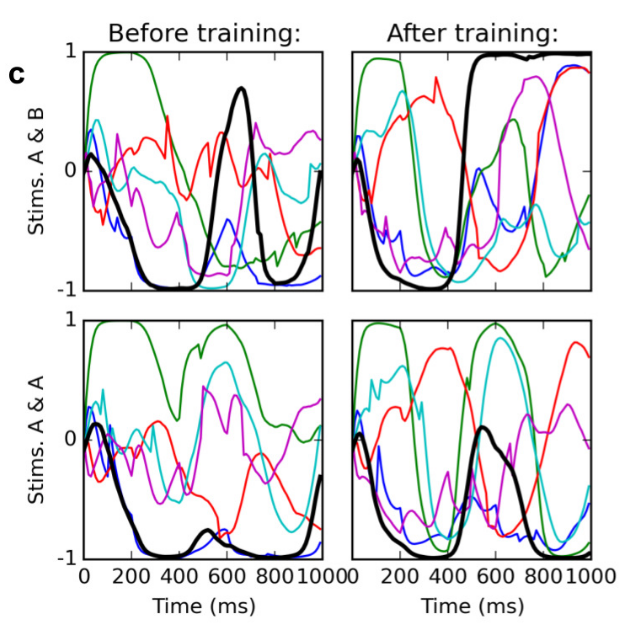
Delayed non-match-to-sample (DNMS) task:
- t = +1 when the cue is different from the sample (AB or BA)
- t = -1 otherwise (AA, BB).
It is a task involving working memory: the first item must be actively remembered in order to produce the response later.
The response is calculated as the mean activity y of the output neuron over the last 200 ms.
The “reward” used is simply the difference between the desired value (t=+1 or -1) and the response:
r = - |t - y|
- The goal is to maximize the sparse reward function, but we know its value only at the end of a trial: temporal credit assignment.
Miconi (2017) Biologically plausible learning in recurrent neural networks reproduces neural dynamics observed during cognitive tasks. eLife 6:e20899.
Reward-modulated Hebbian learning
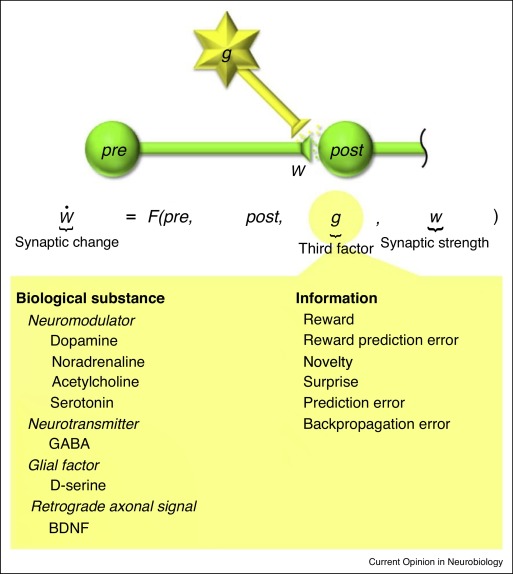
- Reward-modulated Hebbian learning changes weights according to the Hebbian product and the change in reward intake:
\Delta w_{ij} = \eta \, r_i \, r_j \, (R - \bar{R})
- \bar{R} can be a running average of the rewards/returns:
\bar{R} \leftarrow \alpha \, \bar{R} + (1-\alpha) \, R
If more reward than usual is received, the weights between correlated neurons should be increased.
If less reward than usual is received, the weights between correlated neurons should be decreased.
This does not work well with sparse rewards (at the end of a complex sequence).
Kuśmierz et al. (2017) Learning with three factors: modulating Hebbian plasticity with errors. Current Opinion in Neurobiology 46, 170–177.
Weight perturbation
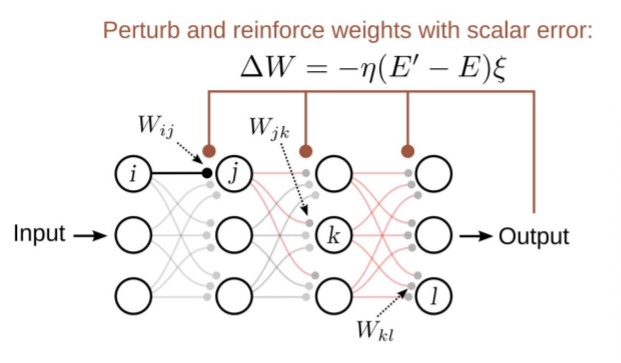
- A simple alternative to backpropagation would consist of adding a perturbation to some weights:
w_{ij} \rightarrow w_{ij} + \xi
and observing the change of reward intake at the end of the episode:
\Delta R = R - \bar{R}
- If the change is positive (the new network gets higher rewards than before), the weight change is conserved. Otherwise it is thrown away or reversed.
\Delta w_{ij} = \eta \, (R - \bar{R}) \, \xi
- Weight perturbation is somehow a way to estimate the gradient of the loss function locally:
\frac{\partial R(\theta)}{\partial w_{ij}} \approx \frac{\Delta R}{\Delta w_{ij}} = \frac{R - \bar{R}}{ w_{ij} + \xi - w_{ij} }
- Core principle of genetic algorithms for NN (e.g. NEAT), but not really biologically realistic…
Node-perturbation
- The post-synaptic potential x_j depends linearly on the weights w_{ij}:
x_j = \ldots + w_{i,j} \, r_i + \ldots
- So instead of perturbing the weight, one could perturb the post-synaptic activity x_j by adding randomly some noise to it \xi_j and observing the change in reward:
x_j \rightarrow x_j + \xi_j
- If a higher postsynaptic activity leads to more reward, then weights from correlated pre-synaptic neurons should be increased:
\Delta w_{ij} = \eta \, (\sum_t r_i \, \xi_j) \, (R - \bar{R})
A trace of the perturbations must be maintained, as learning occurs only at the end of the trial.
Still not biologically plausible: a synapse cannot access and store directly the perturbations, which may come from other neurons.
Fiete and Seung (2006) Gradient learning in spiking neural networks by dynamic perturbation of conductances. Physical Review Letters 97:048104.
Exploratory Hebbian (E-H) learning
- Miconi’s idea was to couple node-perturbation (Fiete et al. 2006) with Exploratory-Hebbian learning (Legenstein et al., 2010).
\Delta w_{ij} = \eta \, r_i \, (x_j - \bar{x_j}) \, (R - \bar{R})
where \bar{x_j} is a running average of the postsynaptic activity (a trace of its activity).
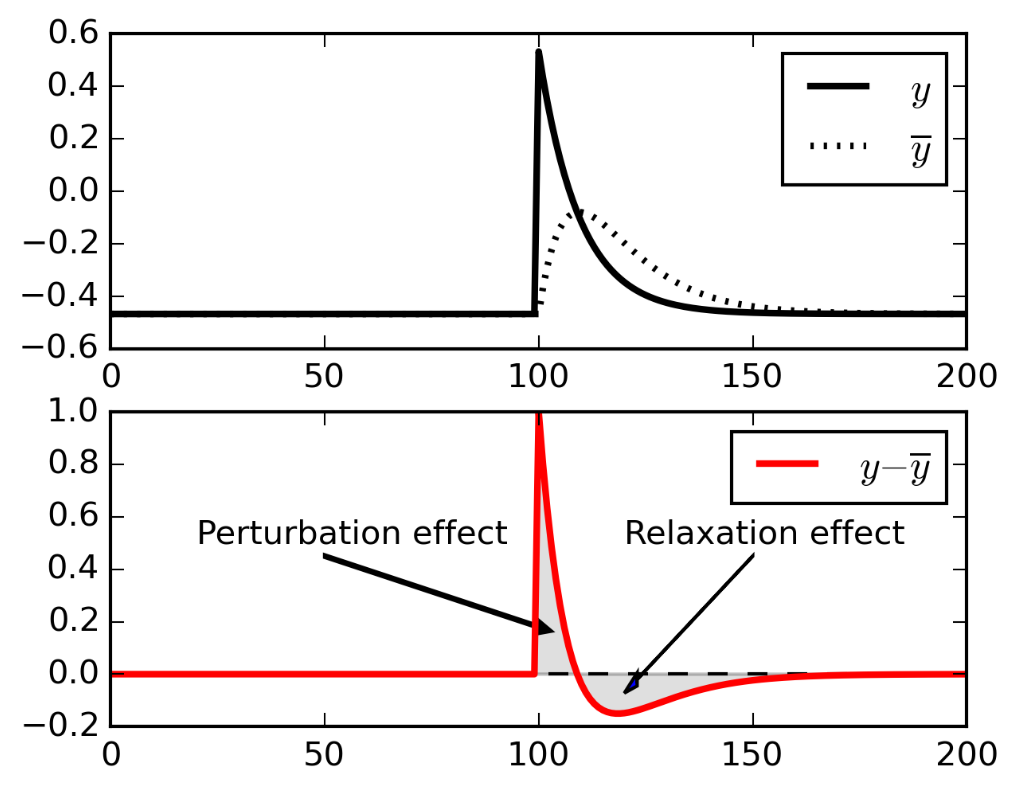
The difference x_j - \bar{x_j} contains information about the perturbation, but is local to the synapse (biologically realistic).
However, the perturbation is canceled by the relaxation. Need for a non-linearity:
\Delta w_{ij} = \eta \, r_i \, (x_j - \bar{x_j})^3 \, (R - \bar{R})
Legenstein et al. (2010) A reward-modulated hebbian learning rule can explain experimentally observed network reorganization in a brain control task. Journal of Neuroscience.
Miconi’s learning rule

- Apply randomly at f=3Hz a perturbation of all the nodes in the reservoir.
x_j \rightarrow x_j + \xi_j
- Maintain a non-linear eligibility trace of the perturbation during the trial.
e_{ij} = e_{ij} + r_i \, (x_j - \bar{x_j})^3
- At the end of the trial, train all weights using the eligibility trace and the change in performance:
\Delta w_{ij} = \eta \, e_{ij} \, (R - \bar{R})
Results : DNMS task
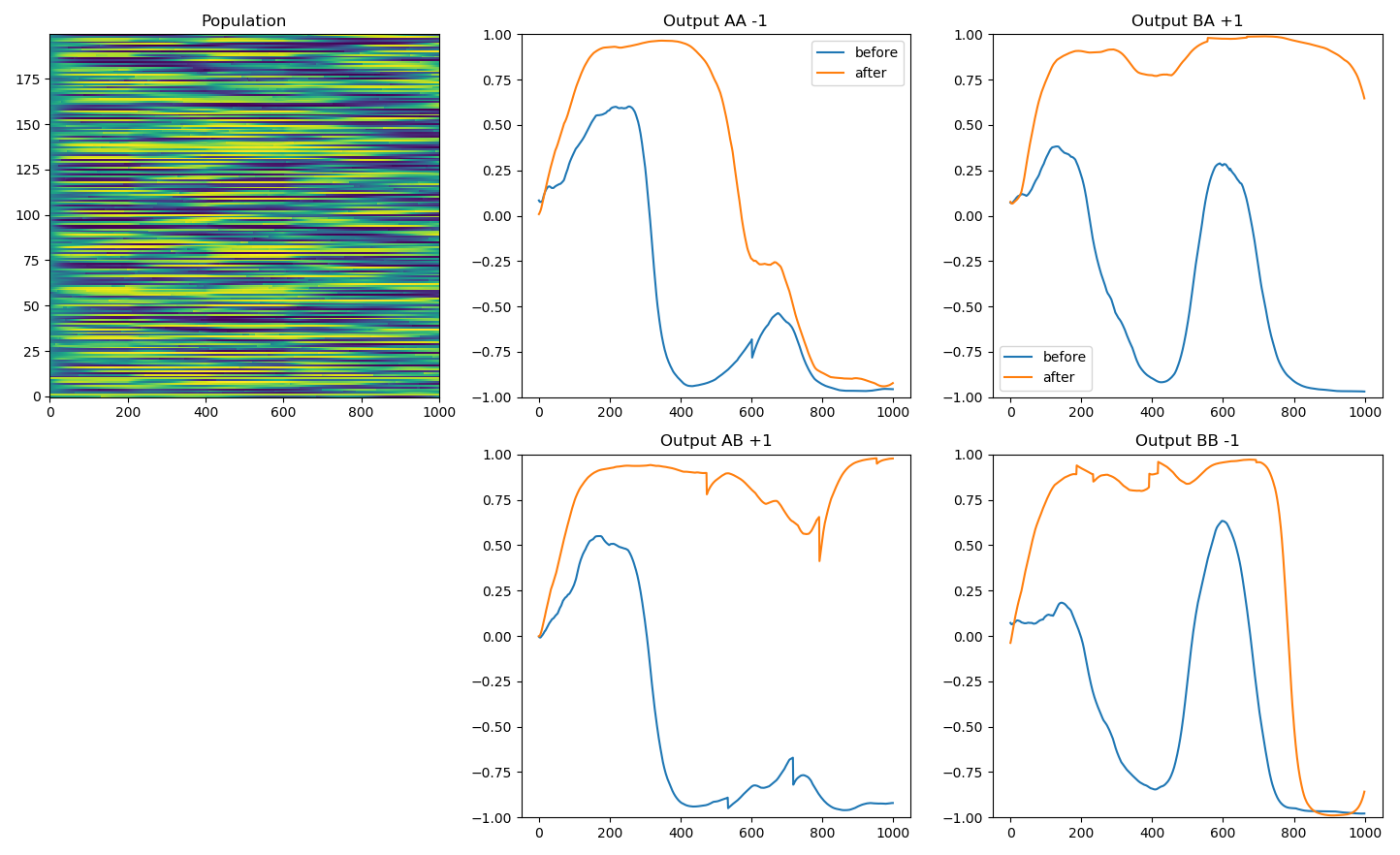
Results : DNMS task
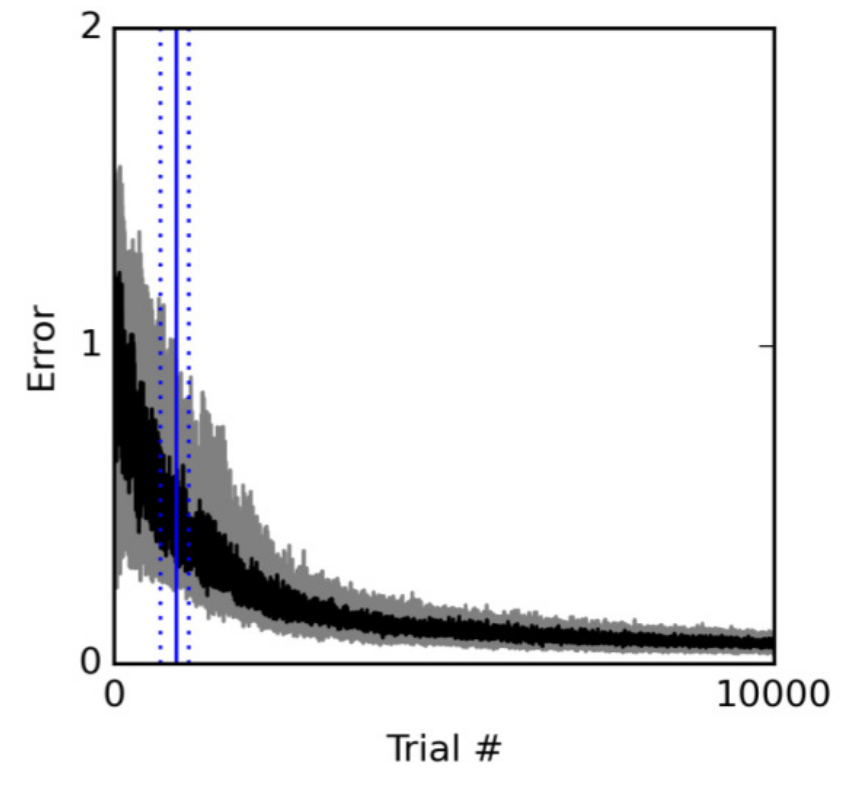
Learning is quite slow (ca 1000 trials), but only from sparse rewards at the end of the trial.
The power of the network does not lie in the readout neurons, but in the dynamics of the reservoir: trajectories are discovered and stabilized using RL.
The only “imperfection” is that learning is actually error-driven, not success-driven:
r = - |t - y|
Results : controlling a robotic arm
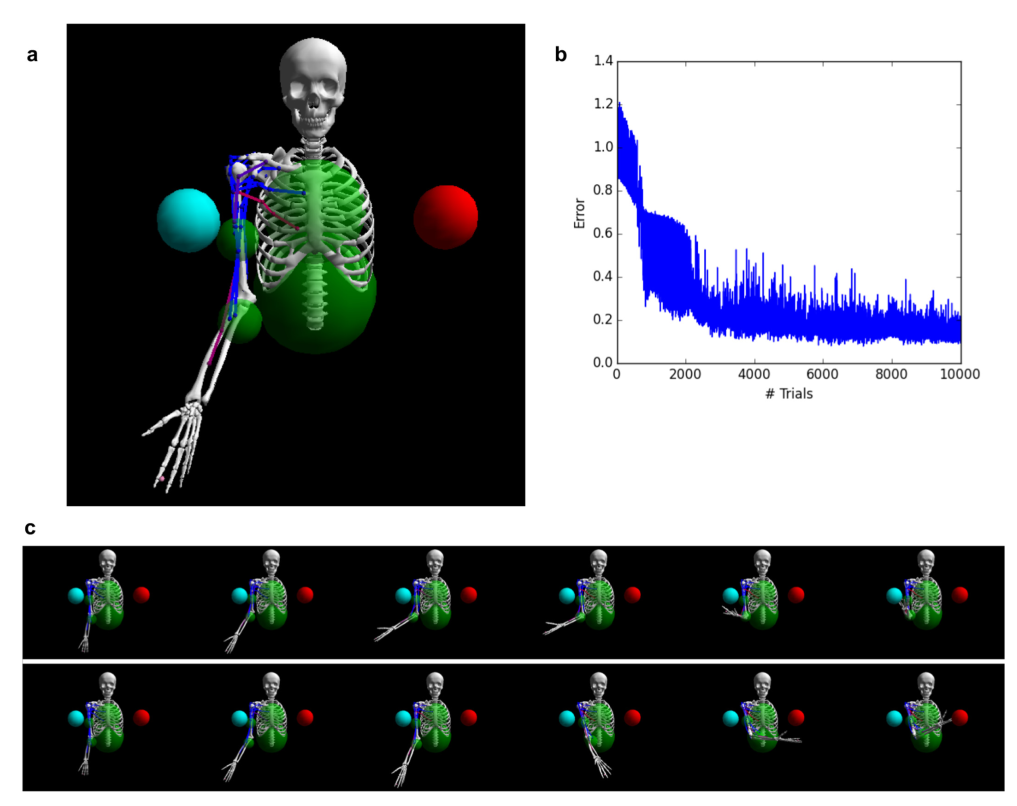
16 motor neurons to control the muscles of an arm.
2 inputs: left / right.
Error is the remaining distance at the end of the trial.
Summary of reservoir computing
- The vanilla formulation of RC with fixed recurrent weights is very powerful compared to classical RNNs (according to LLama3):
- Improved long-term dependencies: RC can learn longer-range dependencies than traditional RNNs, which are limited by their recurrent connections.
- Faster training times: RC typically requires less computation and memory during training compared to RNNs, making it more efficient for large datasets.
- Better handling of sparse data: RC is better suited for dealing with sparse or irregularly sampled time series data, as it doesn’t require fixed-size input sequences like traditional RNNs.
- Improved robustness to noise and outliers: RC has been shown to be more robust to noisy or outlier-filled data due to its ability to learn from a smaller window of past information.
- Reduced overfitting: RC’s architecture can help prevent overfitting by focusing on local patterns in the data, rather than trying to capture long-term dependencies that may not be relevant.
- Improved interpretability: The reservoir’s fixed weights and simple recurrent connections make it easier to understand how the model is processing information, compared to traditional RNNs with complex weight updates.
- Scalability: RC can be applied to larger datasets and more complex tasks than traditional RNNs, thanks to its ability to handle sparse data and improved computational efficiency.
- Learning the recurrent weights to stabilize the dynamics is much more difficult, and requires advanced/expensive optimization methods (RLS) or gradient-free approaches such as RL and evolution.