Neurocomputing
Spiking networks
Professur für Künstliche Intelligenz - Fakultät für Informatik
1 - Spiking neurons
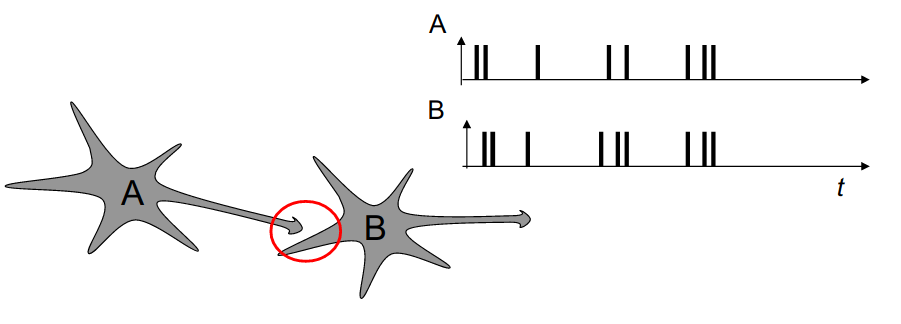
Biological neurons communicate through spikes
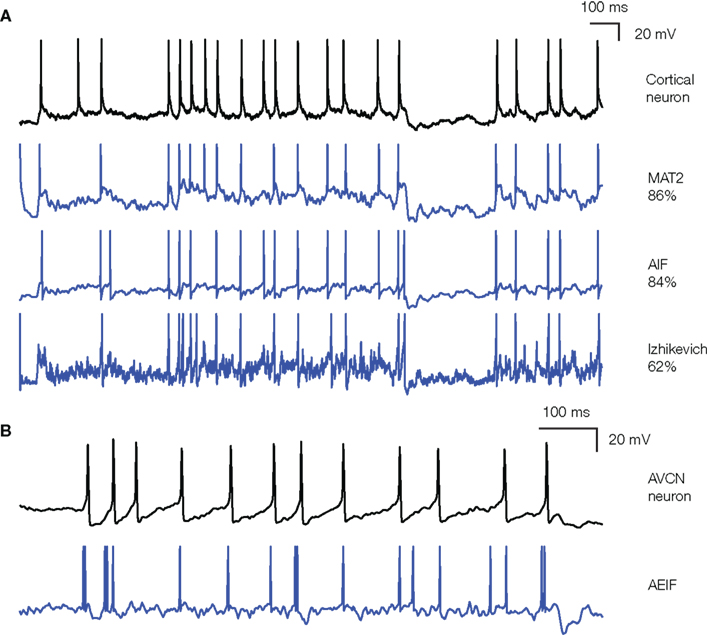
The two important dimensions of the information exchanged by neurons are:
The instantaneous frequency or firing rate: number of spikes per second (Hz).
The precise timing of the spikes.
The shape of the spike (amplitude, duration) does not matter much.
Spikes are binary signals (0 or 1) at precise moments of time.
Rate-coded neurons only represent the firing rate of a neuron and ignore spike timing.
Spiking neurons represent explicitly spike timing, but omit the details of action potentials.
Rossant et al. (2011) Fitting Neuron Models to Spike Trains. Front. Neurosci. 5. doi:10.3389/fnins.2011.00009
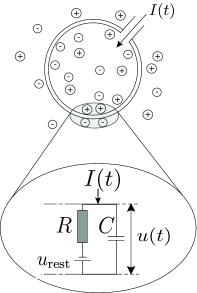
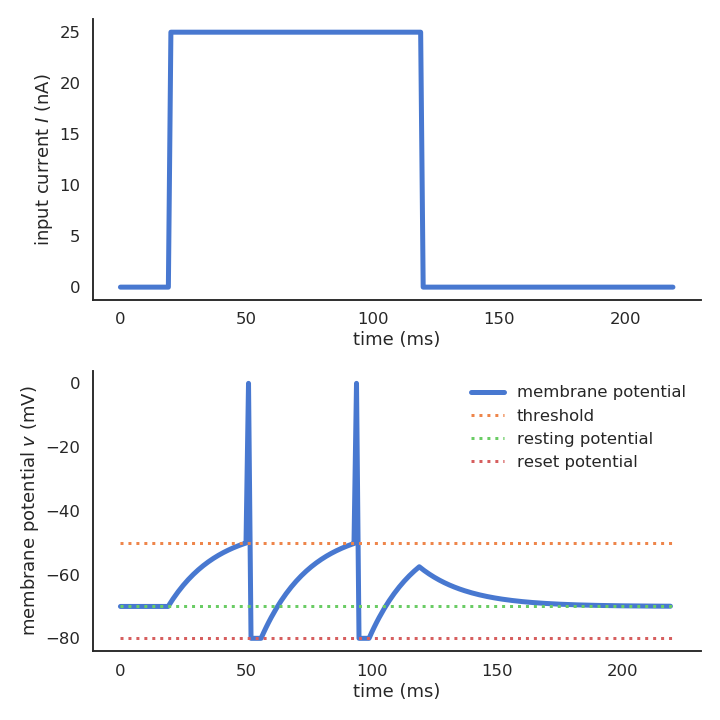
The leaky integrate-and-fire neuron (Lapicque, 1907)
- The leaky integrate-and-fire (LIF) neuron has a membrane potential v(t) that integrates its input current I(t):
C \, \frac{dv(t)}{dt} = - g_L \, (v(t) - V_L) + I(t)
C is the membrane capacitance, g_L the leak conductance and V_L the resting potential.
In the absence of input current (I=0), the membrane potential is equal to the resting potential.
- When the membrane potential exceeds a threshold V_T, the neuron emits a spike and the membrane potential is reset to the reset potential V_r for a fixed refractory period t_\text{ref}.
\text{if} \; v(t) > V_T \; \text{: emit a spike and set} \, v(t) = V_r \; \text{for} \, t_\text{ref} \, \text{ms.}
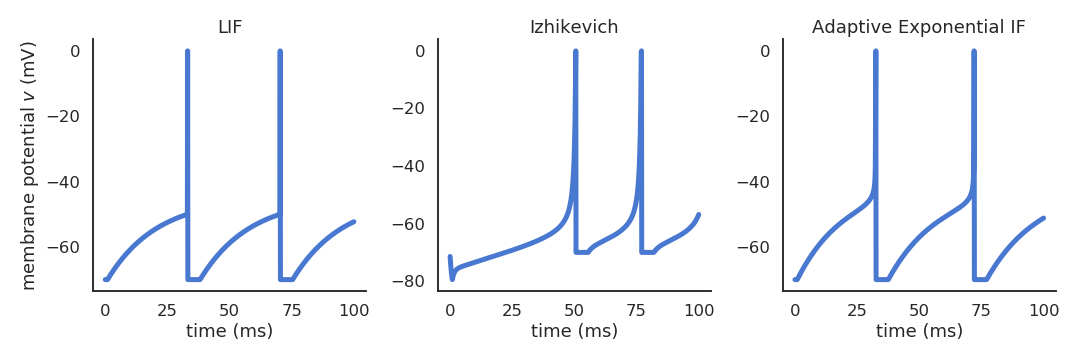
Different spiking neuron models are possible
- Izhikevich quadratic Integrate-and-fire.
\frac{dv(t)}{dt} = 0.04 \, v(t)^2 + 5 \, v(t) + 140 - u(t) + I(t) \frac{du(t)}{dt} = a \, (b \, v(t) - u(t))
Izhikevich (2003) Simple model of spiking neurons. IEEE transactions on neural networks 14:1569–72. doi:10.1109/TNN.2003.820440
Different spiking neuron models are possible
- Adaptive exponential IF (AdEx).
C \, \frac{dv(t)}{dt} = -g_L \ (v(t) - E_L) + g_L \, \Delta_T \, \exp(\frac{v(t) - v_T}{\Delta_T}) + I(t) - w \tau_w \, \frac{dw}{dt} = a \, (v(t) - E_L) - w

Brette and Gerstner (2005) Adaptive Exponential Integrate-and-Fire Model as an Effective Description of Neuronal Activity. Journal of Neurophysiology 94:3637–3642.
Realistic neuron models can reproduce a variety of dynamics
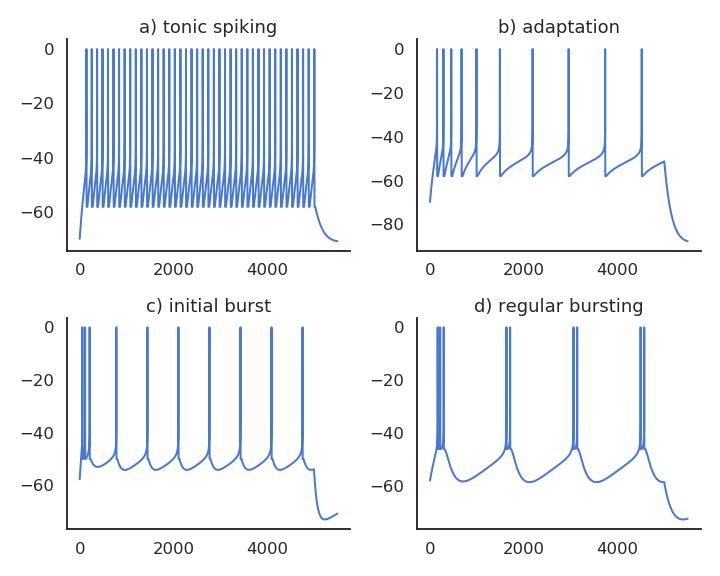
Biological neurons do not all respond the same to an input current.
Some fire regularly.
Some slow down with time.
Some emit bursts of spikes.
Modern spiking neuron models allow to recreate these dynamics by changing a few parameters.
Synaptic transmission
- Spiking neurons communicate by increasing the conductance g_e of the postsynaptic neuron:
C \, \frac{dv(t)}{dt} = - g_L \, (v(t) - V_L) - g_e(t) \, (v(t) - V_E) + I(t)
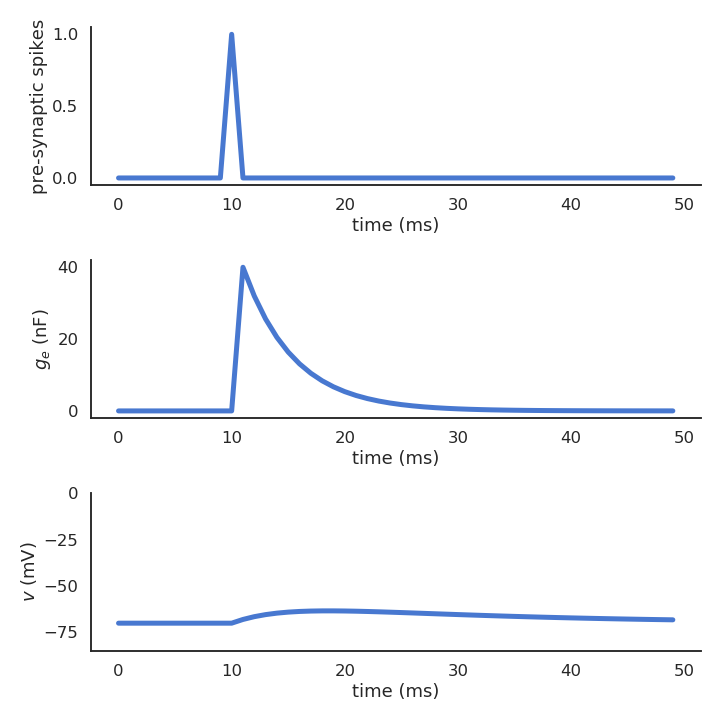
- Incoming spikes increase the conductance from a constant w which represents the synaptic efficiency (or weight):
g_e(t) \leftarrow g_e(t) + w
- If there is no spike, the conductance decays back to zero:
\tau_e \, \frac{d g_e(t)}{dt} + g_e(t) = 0
- An incoming spike temporarily increases (or decreases if the weight w is negative) the membrane potential of the post-synaptic neuron.
Synaptic transmission
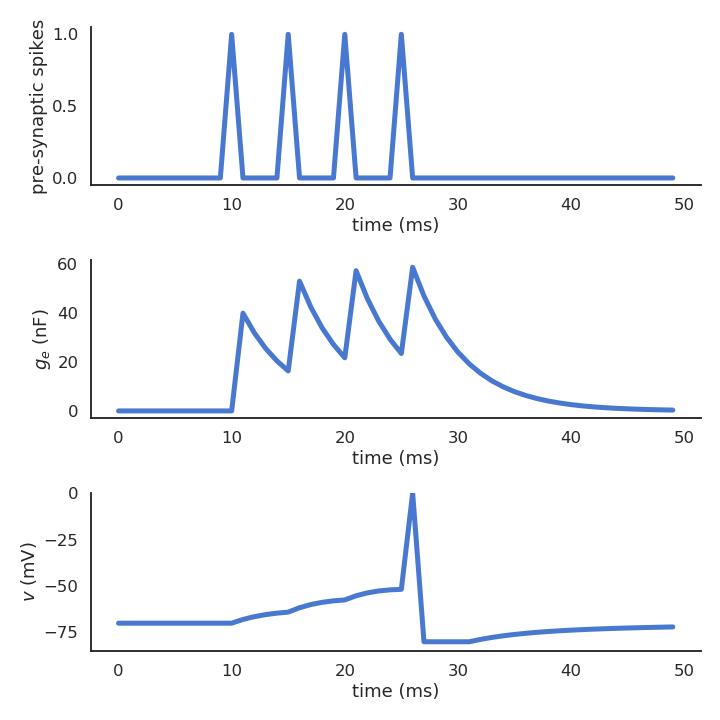
When enough spikes arrive at the post-synaptic neuron close in time:
either one pre-synaptic fires very rapidly,
or many different pre-synaptic neurons fire in close proximity,
this can be enough to bring the post-synaptic membrane over the threshold, so that it it turns emits a spike.
This is the basic principle of synaptic transmission in biological neurons.
- Neurons emit spikes, which modify the membrane potential of other neurons, which in turn emit spikes, and so on.
Populations of spiking neurons
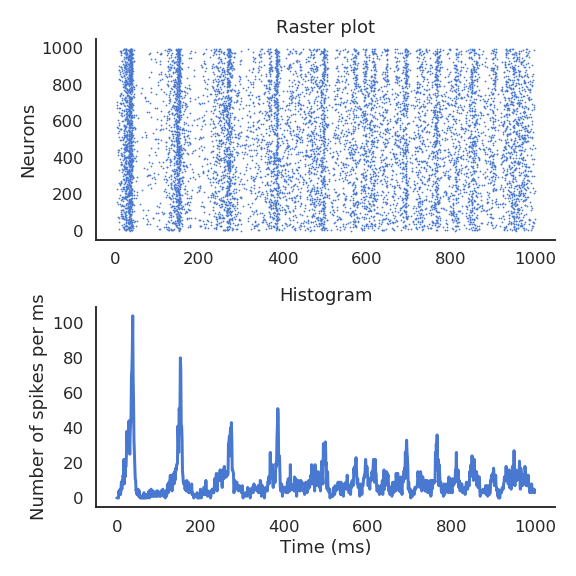
- Recurrent networks of spiking neurons exhibit various dynamics.
They can fire randomly, or tend to fire synchronously, depending on their inputs and the strength of the connections.
Liquid State Machines are the spiking equivalent of echo-state networks.
Hebbian learning
- Hebbian learning postulates that synapses strengthen based on the correlation between the activity of the pre- and post-synaptic neurons:
When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased. Donald Hebb, 1949
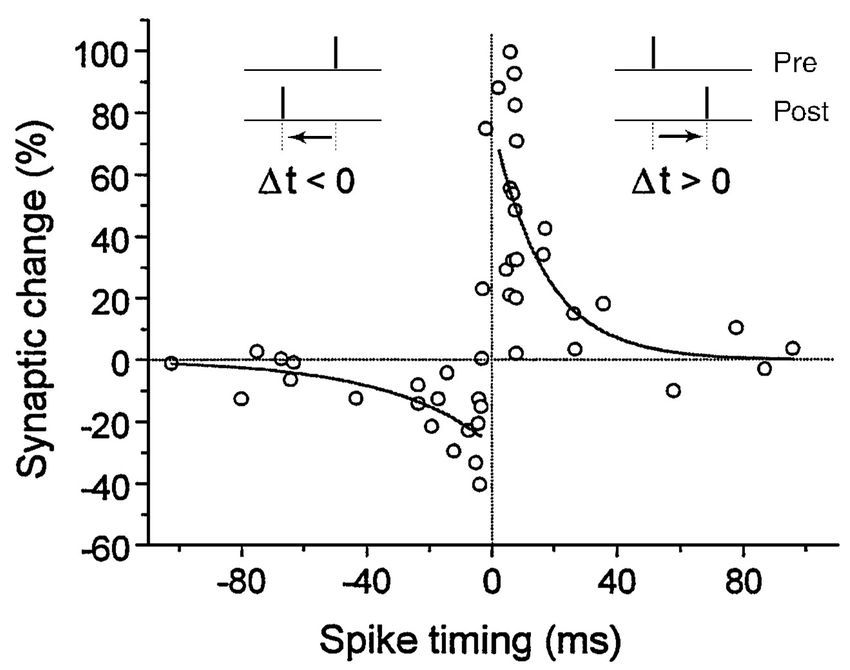
STDP: Spike-timing dependent plasticity
Synaptic efficiencies actually evolve depending on the the causation between the neuron’s firing patterns:
If the pre-synaptic neuron fires before the post-synaptic one, the weight is increased (long-term potentiation). Pre causes Post to fire.
If it fires after, the weight is decreased (long-term depression). Pre does not cause Post to fire.
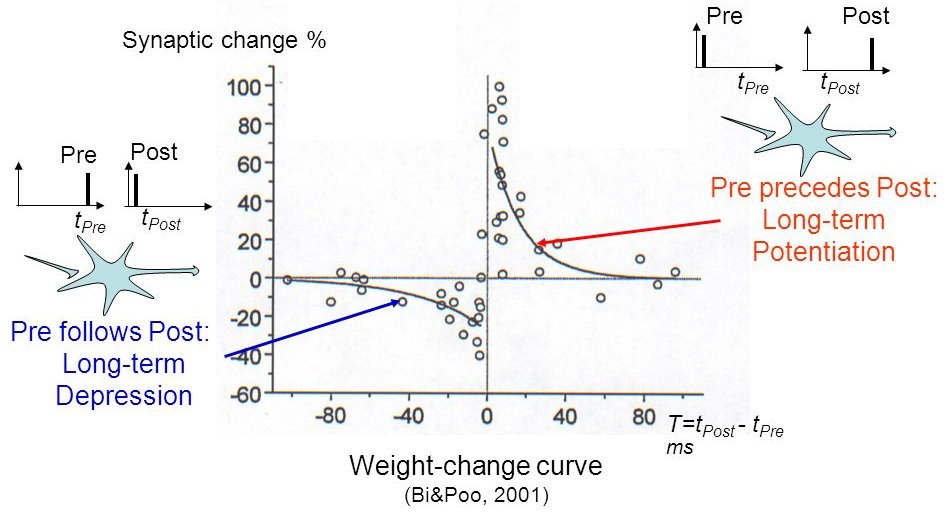
Bi and Poo (2001) Synaptic modification of correlated activity: Hebb’s postulate revisited. Ann. Rev. Neurosci., 24:139-166.
STDP: Spike-timing dependent plasticity
- The STDP (spike-timing dependent plasticity) plasticity rule describes how the weight of a synapse evolves when the pre-synaptic neuron fires at t_\text{pre} and the post-synaptic one fires at t_\text{post}.
\Delta w = \begin{cases} A^+ \, \exp - \frac{t_\text{pre} - t_\text{post}}{\tau^+} \; \text{if} \; t_\text{post} > t_\text{pre}\\ A^- \, \exp - \frac{t_\text{pre} - t_\text{post}}{\tau^-} \; \text{if} \; t_\text{pre} > t_\text{post}\\ \end{cases}
STDP can be implemented online using traces.
More complex variants of STDP (triplet STDP) exist, but this is the main model of synaptic plasticity in spiking networks.
Bi and Poo (2001) Synaptic modification of correlated activity: Hebb’s postulate revisited. Ann. Rev. Neurosci., 24:139-166.
2 - Deep convolutional spiking networks

Kheradpisheh et al. (2018) STDP-based spiking deep convolutional neural networks for object recognition. Neural Networks 99, 56–67.
Deep convolutional spiking networks
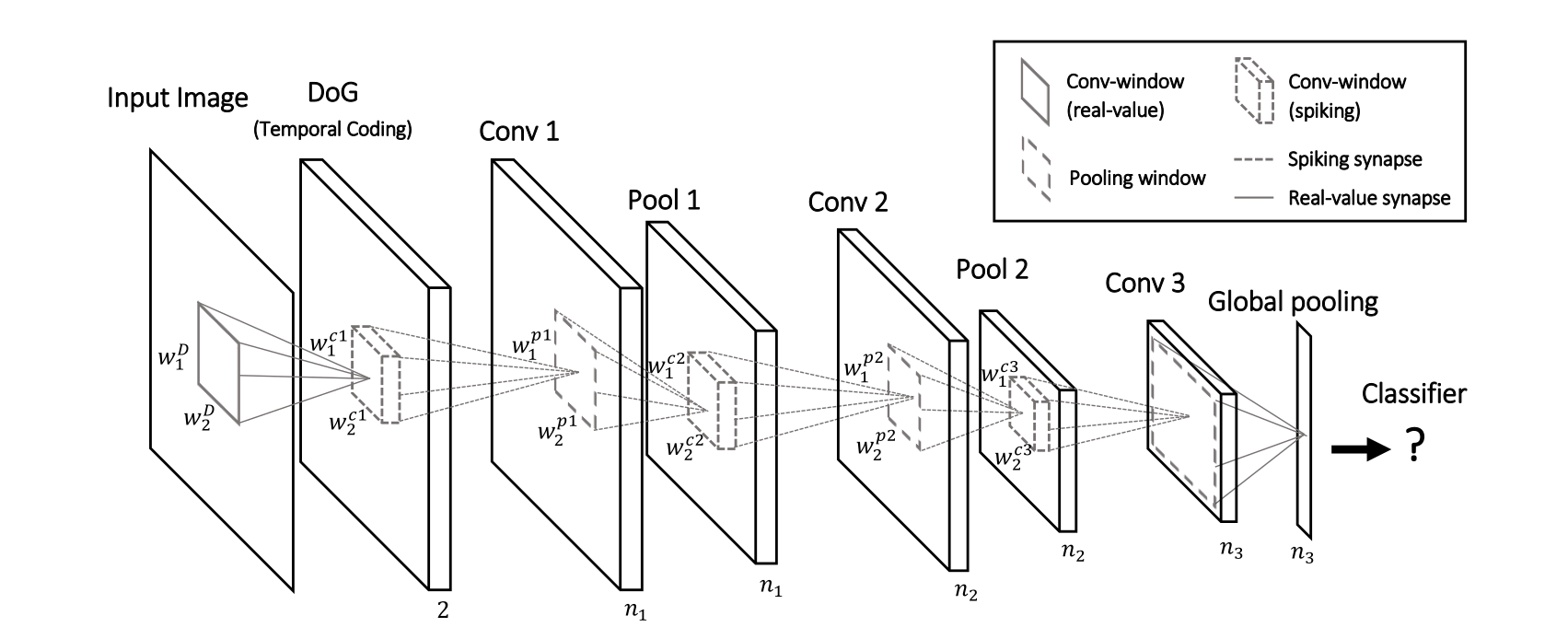
A lot of work has lately focused on deep spiking networks, either using a modified version of backpropagation or using STDP.
The Masquelier lab has proposed a deep spiking convolutional network learning to extract features using STDP (unsupervised learning).
A simple classifier (SVM) then learns to predict classes.
Kheradpisheh et al. (2018) STDP-based spiking deep convolutional neural networks for object recognition. Neural Networks 99, 56–67.
Deep convolutional spiking networks
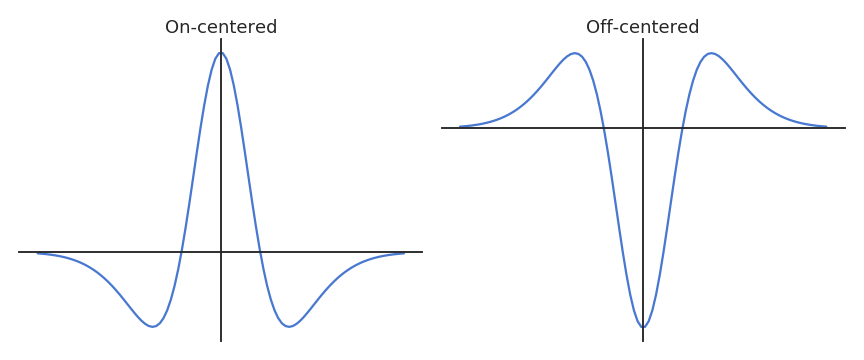
The image is first transformed into a spiking population using difference-of-Gaussian (DoG) filters.
On-center neurons fire when a bright area at the corresponding location is surrounded by a darker area.
Off-center cells do the opposite.
Kheradpisheh et al. (2018) STDP-based spiking deep convolutional neural networks for object recognition. Neural Networks 99, 56–67.
Deep convolutional spiking networks

The convolutional and pooling layers work just as in regular CNNs (shared weights), except the neuron are integrate-and-fire (IF).
There is additionally a temporal coding scheme, where the first neuron to emit a spike at a particular location (i.e. over all feature maps) inhibits all the others.
This ensures selectivity of the features through sparse coding: only one feature can be detected at a given location.
STDP allows to learn causation between the features and to extract increasingly complex features.
Kheradpisheh et al. (2018) STDP-based spiking deep convolutional neural networks for object recognition. Neural Networks 99, 56–67.
Deep convolutional spiking networks

Deep convolutional spiking networks
Deep convolutional spiking networks
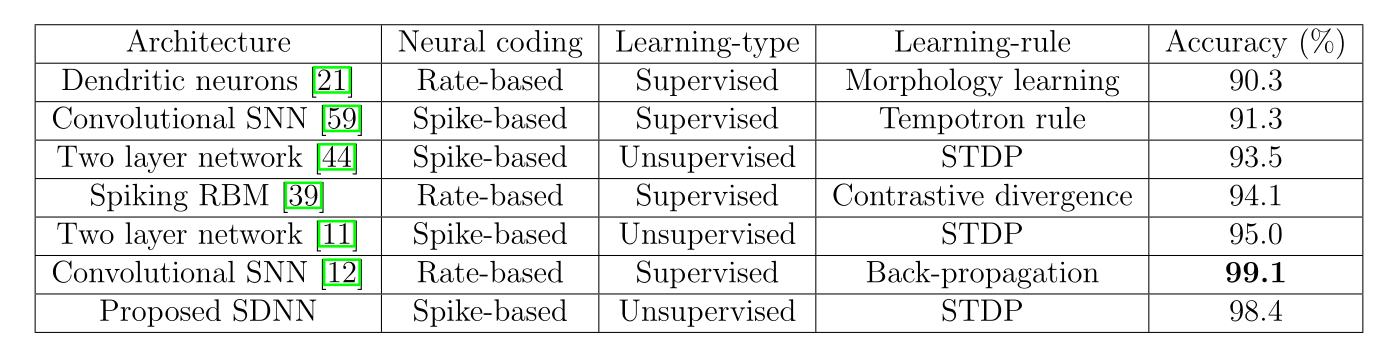
The network is trained unsupervisedly on various datasets and obtains accuracies close to the state of the art:
- Caltech face/motorbike dataset.
- ETH-80
- MNIST

Kheradpisheh et al. (2018) STDP-based spiking deep convolutional neural networks for object recognition. Neural Networks 99, 56–67.
Deep convolutional spiking networks
- The performance on MNIST is in line with classical 3-layered CNNs, but without backpropagation!
Kheradpisheh et al. (2018) STDP-based spiking deep convolutional neural networks for object recognition. Neural Networks 99, 56–67.
3 - Neuromorphic computing
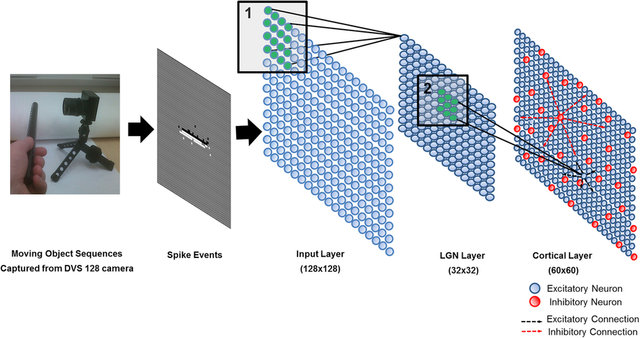
Event-based cameras
Event-based cameras
Event-based cameras
Neuromorphic computing
Event-based cameras are inspired from the retina (neuromorphic) and emit spikes corresponding to luminosity changes.
Classical computers cannot cope with the high fps of event-based cameras.
Spiking neural networks can be used to process the events (classification, control, etc). But do we have the hardware for that?
Intel Loihi
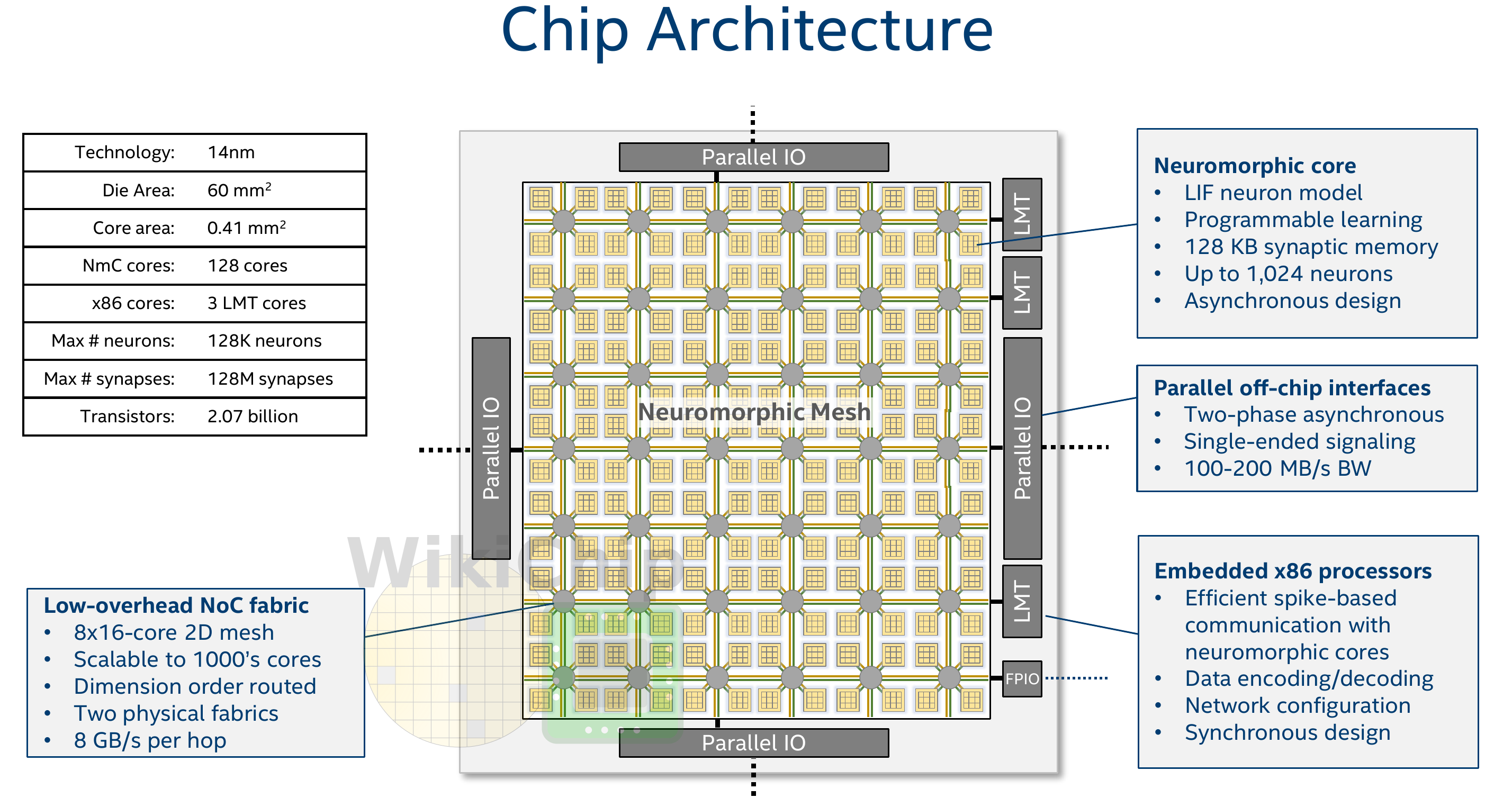
Intel Loihi
- Loihi implements 128 neuromorphic cores, each containing 1,024 primitive spiking neural units grouped into tree-like structures in order to simplify the implementation.
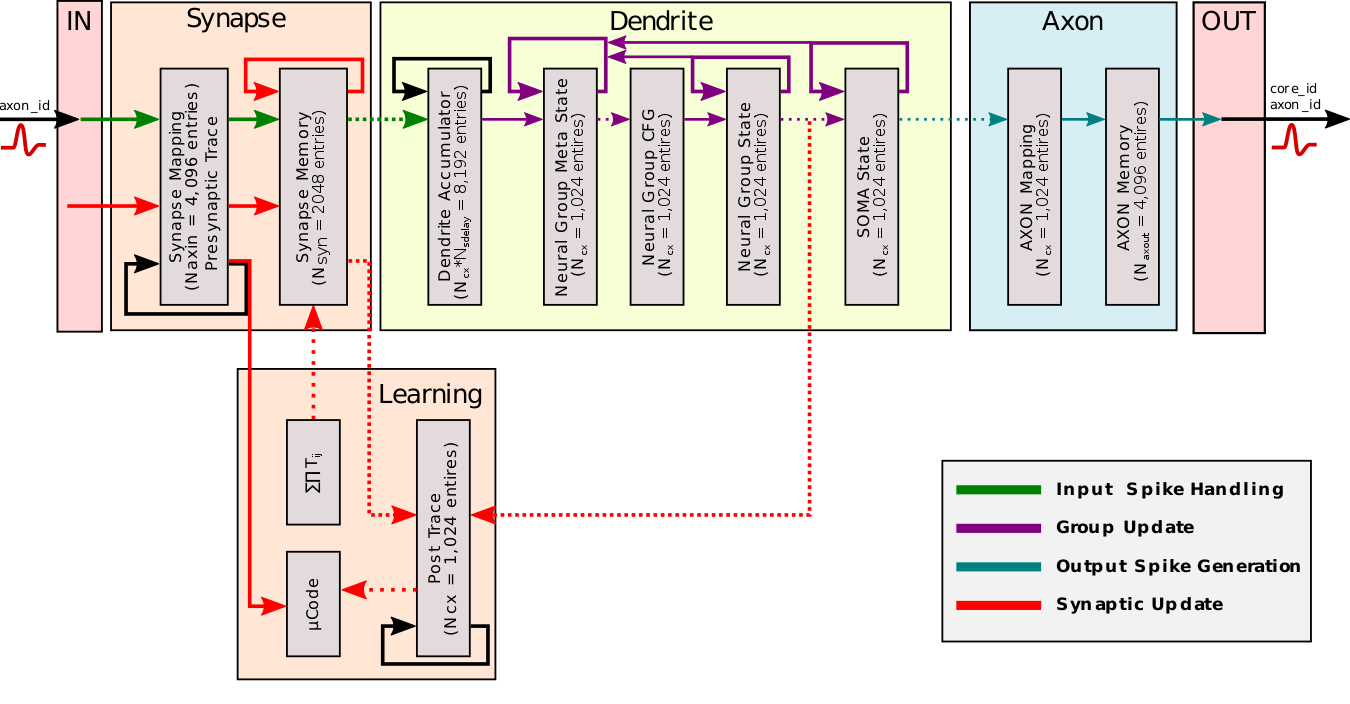
Intel Loihi
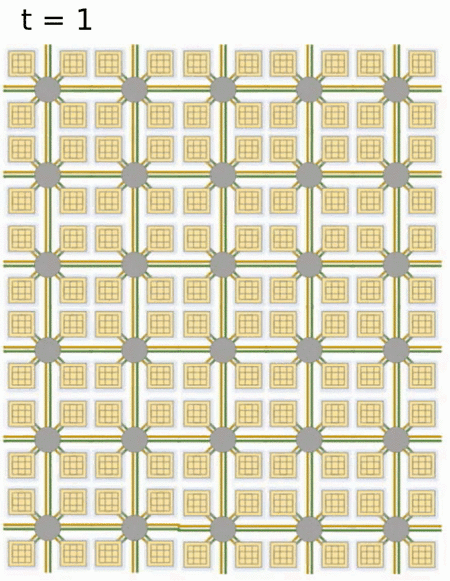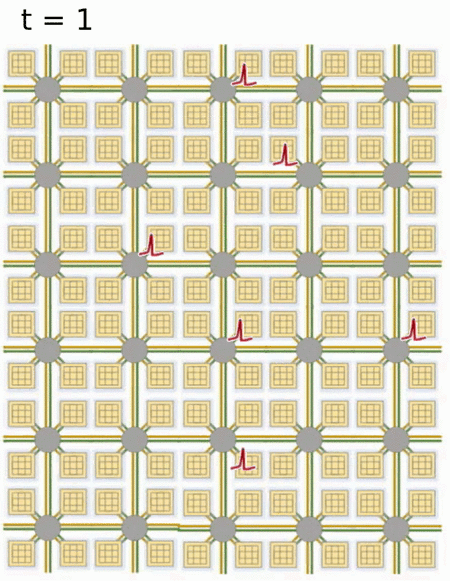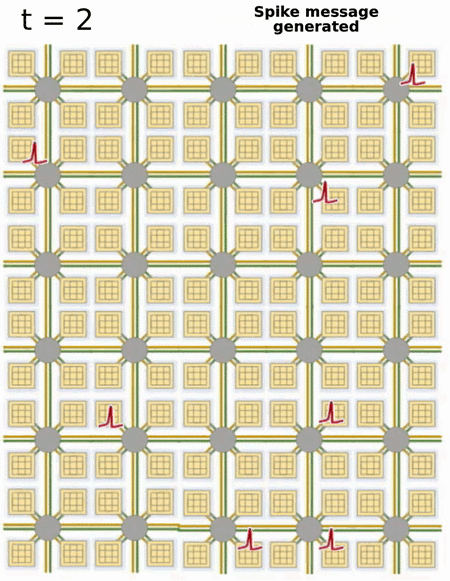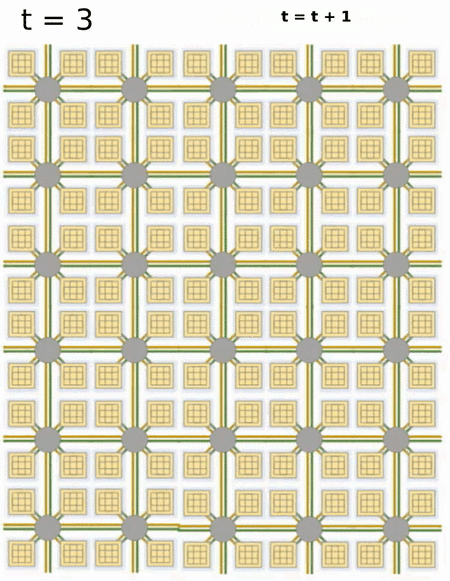
Each neuromorphic core transits spikes to the other cores.
Fortunately, the firing rates are usually low (10 Hz), what limits the communication costs inside the chip.
Synapses are learnable with STDP mechanisms (memristors), although offline.
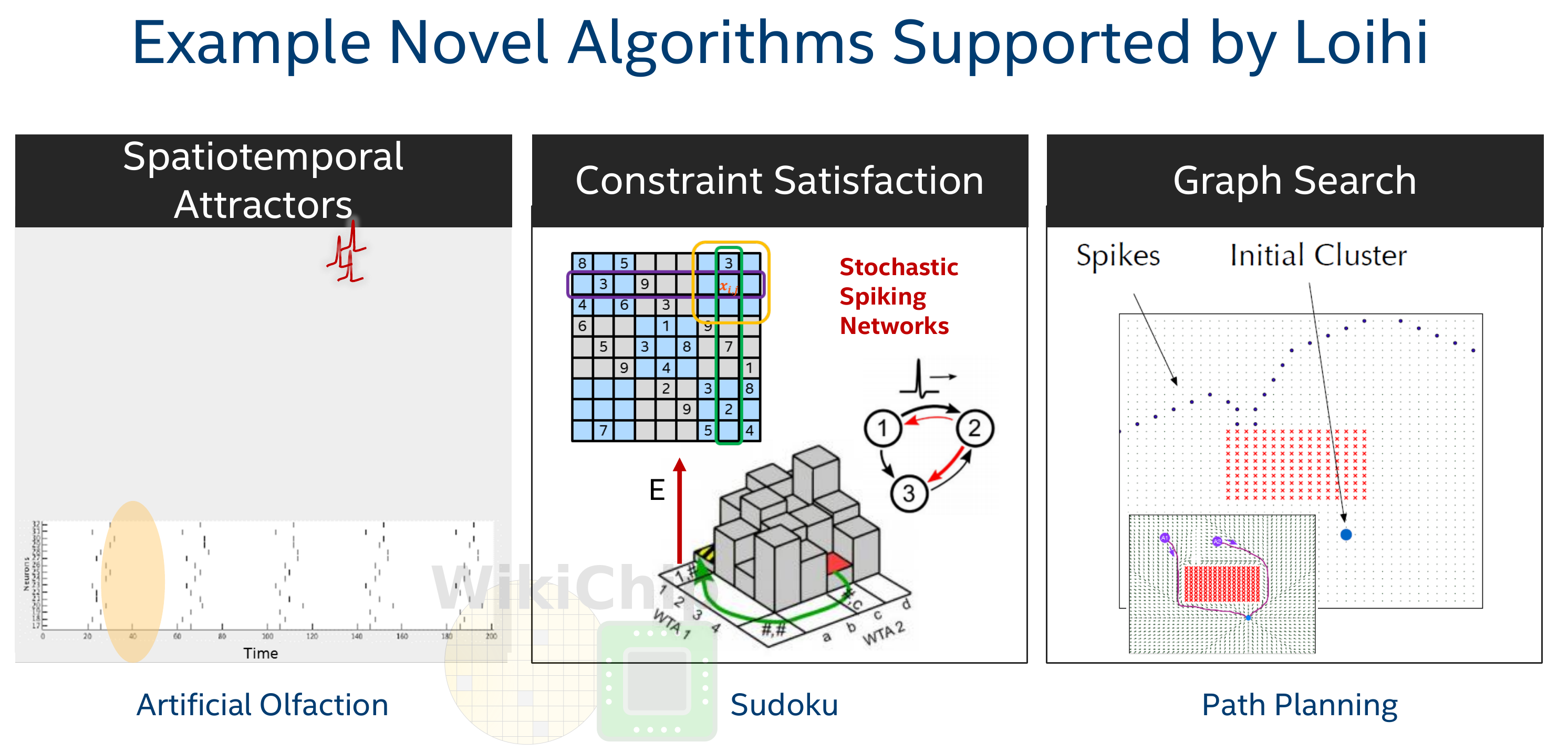
Neuromorphic computing
Intel Loihi consumes 1/1000th of the energy needed by a modern GPU.
Alternatives to Intel Loihi are:
IBM TrueNorth
Spinnaker (University of Manchester).
Brainchip
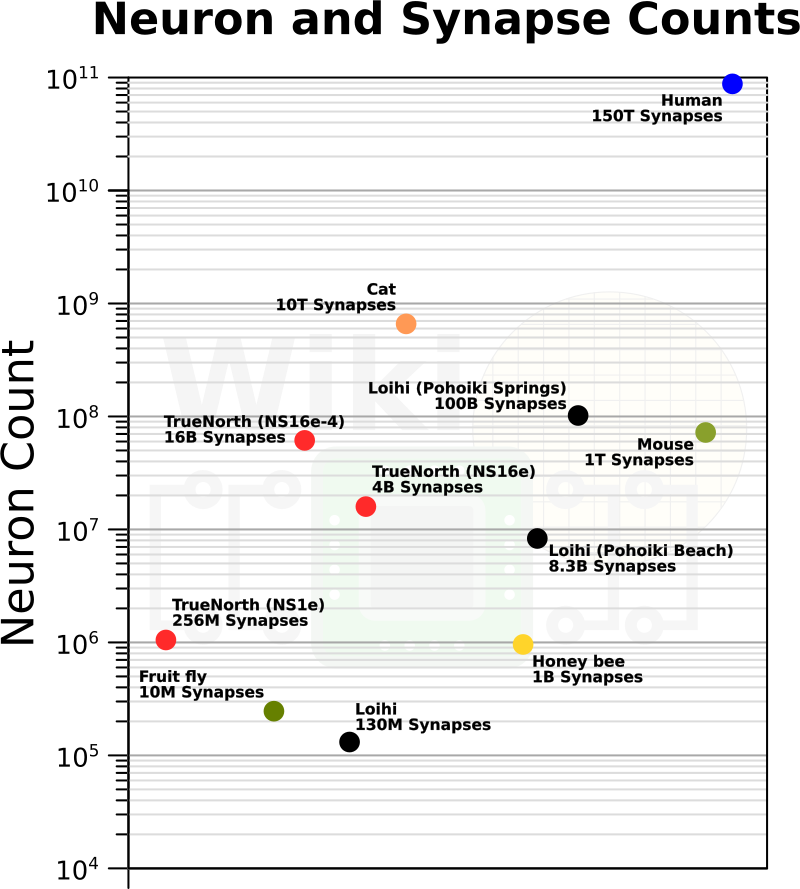
The number of simulated neurons and synapses is still very far away from the human brain, but getting closer!