1 Introduction
Minsky (1968) defined the field of Artificial Intelligence (AI) as “the science of making machines do things that would require intelligence if done by humans”. Over its almost 70 years of existence - John MacCarthy invented the term in 1956 -, AI has achieved a lot of progress in specialized areas such as data-mining, machine learning, computer vision, speech recognition or even single cognitive tasks such as chess playing or medical diagnosis. Weak (or applied) AI indeed focuses on methods allowing to solve specific tasks which either necessitate a limited range of human intellectual abilities (e.g. recognizing objects) or even have nothing to do with human intelligence (e.g. search engines). Although these improvements have proven very useful, especially in an industrial context, the real goal of AI - called strong AI by Searle (1980) - is to obtain systems with a general form of intelligence that could be compared with human intelligence on complex behaviors. Despite recent advances in machine learning techniques (e.g. deep learning, LeCun et al., 2015) and prophetic claims that the singularity is approaching (Kurzweil, 2005), one has to admit that strong AI has basically failed until now (Velik, 2012). As Marvin Minsky noticed, all we have is a collection of “dumb” specialists which perform single tasks very well - deep neural networks exceed for example human performance on certain visual recognition tasks - but which, when put together, do not even get close to the cognitive abilities of a rodent. Robotic competitions such as RoboCup are good demonstrators of the limits of strong AI.
Many cognitive architectures for strong AI have been proposed over the years (for a review, see Langley et al., 2009). They usually take the form of conversational agents, virtual reality avatars or robotic platforms, although they may also be used in specific applications. They can be classified generally into two approaches: the symbolic (or cognitivist) approach, which breaks human intelligence into functional components - e.g. attention, long-term memory, sensory processes - and implements each of them with particular symbolic algorithms - production rules, tree searches; and the connectionnist (or emergentist) approach which considers distributed systems of functional units (often in the form of neural networks) which interact with each other and learn to perform a task through interacting with an environment. Although the behavior of a symbolic system is easier to analyze, its suitability for real-world problems is problematic: if breaking a task into elementary components makes sense for symbolic problems such as the game of chess, it becomes much harder for recognizing a face, engaging a conversation appropriately or even playing football. The main issue here is symbol-grounding: while manipulating the concept of a cup or a ball is easy for a computer, it is much harder to relate this concept to the visual perception of a cup or ball with any possible shape, under various lightning conditions or orientations. This explains why symbolic cognitive architectures have mostly failed to produce interesting behaviors outside restricted lab settings. An additional difficulty is the amount of work required to create the cognitive architecture: each module of the system must communicate symbols adequately to the others, which in turn should be able to cope with potential failures. The resulting architecture becomes quickly tuned to a particular problem, and any significant change in the environmental conditions may require to redevelop the whole system.
The connectionnist approach relies heavily on learning to exhibit the desired cognitive functions. Contrary to symbolic architectures, the desired function is not hard-coded in the system but rather emerges from the interaction of multiple units after learning. An example is artificial neural networks, where neurons communicate with each other through connections whose weights evolve with learning: the function performed arises from this interaction, not from the structure of the network itself. The same network can for example learn to perform many different functions, depending on its interaction with the task. The computational properties of neural networks are heavily used in weak AI, especially in machine learning. The drawback of this decoupling between the function and the underlying structure is that it becomes complicated to create complex cognitive architectures: the communication between different modules is not symbolic anymore, but numerical - the activity of a population of neurons. Psychological models of cognition, using generic modules such as planning or long-term memory, do not map easily on a connectionnist substrate.
To overcome this problem, a promising direction for AI is to get inspiration from the only truly intelligent system known to date: the brain. The brain has intrinsically a connectionnist structure: it is composed of hundreds of billions of neurons, communicating with each other through synapses which undergo plasticity based on experience. The core idea of brain-like AI (or brain-inspired AI) is to study how the brain exhibits natural intelligence and extract the necessary mechanisms to reproduce it in an artificial system. Velik (2012) defined the basic dogma of brain-like AI as such:
It is well appreciated that the human brain is the most sophisticated, powerful, efficient, effective, flexible and intelligent information processing system known. Therefore, the functioning of the human brain, its structural organization, and information processing principles should be used as archetype for designing artificial intelligent systems instead of just emulating its behavior in a black box manner. To achieve this, approaches should not build on work from engineers only but on a close cooperation between engineers and brain scientists.
Brain-like AI covers a variety of approaches, from top-down models simulating the functions of particular brain areas using non-brain-inspired implementations (e.g. Bayesian models for decision making), to bottom-up models simulating with great detail specific brain areas, but without any relationship to their function (e.g. Human Brain Project). The neuro-computational models presented in this thesis aim at finding a middle ground between these approaches: address the problem of intelligence at the functional level (the models should be useful at the end), while keeping the biological realism high enough to explain and predict biological neural mechanisms. This link between function and structure in the brain is the fundamental question of computational neuroscience, which partly overlaps with brain-like AI. Neuro-computational models in this field are by design close to the architecture of the brain; insights from neuroscience on motivated behavior can be rapidly integrated to improve both their plausibility and performance. They furthermore provide an unique way to investigate new computing paradigms.
1.1 Computational neuroscience
Aim
The ambition of computational neuroscience is to bring a computational modeling approach to the interdisciplinary field of neuroscience, aiming concurrently at an explicative role - explaining why the brain behaves in the observed way - and a predictive one - suggesting previously unobserved effects which can be tested. The main challenge is to integrate experimental observations from different levels of description (neuroanatomy, neurochemistry, neurophysiology, neuro-imaging, cognitive science and behavioral studies) into a biologically realistic neural network. Numerical simulations of this model allow to reproduce the underlying observations in a systematic way and to better analyze, interpret and understand the available data. Conversely, predictions can be made based on these simulations, guiding experimentalists in the design of their experiments (theory-driven neuroscience).
Although the term was only first coined by Eric L. Schwartz in 1985, the first examples of computational neuroscience work may be the invention of the integrate-and-fire neuron by Lapicque (1907) and the complete mathematical characterization of the initiation and propagation of action potentials in the squid giant axon by Hodgkin and Huxley (1952). Research in computational neuroscience has long focused mostly on characterizing the dynamics of individual neurons or small assemblies. The focus has now shifted toward large-scale models, either at the systems level where functional networks involved in particular processes are investigated (Dranias et al., 2008; Hamker, 2004), or at the detailed biological level, with the goal of simulating complete brain areas, as in the Blue Brain Project (Markram, 2006), or even the whole brain in its follower Human Brain Project (HBP). Neuro-computational models have virtually addressed over the years all brain structures and functions, including vision in the occipital and temporal lobes (Rolls and Deco, 2001), working memory in the prefrontal cortex and basal ganglia (Frank et al., 2001; Schroll et al., 2012), long-term memory formation in the hippocampal formation (Burgess et al., 2007) or motor learning in the cerebellum (Albus, 1971).
Neuro-computational models
Neuro-computational models typically study the interaction of different brain areas. Each area comprises a certain number of artificial neurons, which are modeled differently depending on the physiological properties of the corresponding biological neuron (pyramidal neuron, medium spiny neuron, basket cell, etc) and the neuro-transmitter they use (e.g. AMPA, NMDA, GABA). Many models however use only two types of neurons: excitatory and inhibitory neurons. When active, excitatory neurons increase the firing rate of neurons receiving synapses from them, while inhibitory neurons decrease it. One of the simplest -although powerful - neuron model is the rate-coded neuron, which computes an instantaneous firing rate (corresponding to the frequency of spike emission at a given time t) and exchange it with other neurons. A rate-coded neuron is described by an ordinary differential equation (ODE), which can be of the form:
\tau \cdot \frac{d r(t)}{dt} + r(t) = \sum_{i \in \text{Exc}} w_i \cdot r_i(t) - \sum_{j \in \text{Inh}} w_j \cdot r_j(t) + B
r(t) is the instantaneous firing rate of a single neuron, \tau the time constant defining the speed of its dynamics and B its baseline activity (the firing rate it has without inputs). Inputs are represented by the weighted sums, where each connection to the neuron (a synapse) has a weight w (also called the synaptic efficiency) which multiplies the firing rate of the corresponding pre-synaptic neuron. Two sums are represented here (corresponding to excitatory and inhibitory synapses, as denoted by their respective positive and negative signs), but more complex relationships can be used. For example, modulatory inputs can multiply globally a weighted sum of excitatory inputs. Additionally, a transfer function can be used to restrict the firing rate to positive values, or implement non-linear effects.
If the description of a single neuron is relatively simple, the computational power of a neuro-computational model comes from the interconnection of several populations of neurons, allowing the emergence of complex functions. The projection of a population on another can be dense (all-to-all, i.e. each neuron in the post-synaptic population has a synapse with every neuron in the pre-synaptic one) or sparse (a synapse exists according to a fixed probability or some more complex rule). Moreover, synaptic plasticity allows to modify the weights w of a projection based on the activity of the neurons, forming the basis of learning in a neural network. The simplest and most famous rule for synaptic plasticity is the Hebbian learning rule (Hebb, 1949), which states that the weight of a synapse increases when both pre- and post-synaptic neurons are active at the same time (correlation-based learning rule):
\Delta w = \eta \cdot r^\text{pre} \cdot r^\text{post}
where w is the weight of the synapse, \eta a learning rate defining the speed of learning, r^\text{pre} and r^\text{post} the instantaneous firing rate of the pre- and post-synaptic neurons, respectively. The disadvantage of this rule being that the weights would increase infinitely, several variants have since been introduced, among which the Oja learning rule (which adds a regularization term to keep the sum of weights coming to a neuron constant, Oja, 1982) or the Bienenstock-Cooper-Munro rule(BCM, modeling both long-term potentiation - LTP, weight increase - and long-term depression - LTD, weight decrease - Bienenstock et al., 1982), as well as rules modeling the modulatory influence of dopamine on synaptic plasticity. Although there is flexibility in the choice of the rules, a hard constraint to obtain a biologically-realistic model is that all the information needed by the rule should be local to the synapse: the weight change can only depend on variables of the pre- and post-synaptic neurons, but not other neurons. Many classical machine learning algorithms such as backpropagation (Rumelhart et al., 1986) can not be used in this context.
Computer science
The cross-fertilization between computational neuroscience and artificial intelligence is well documented. As explained later, reinforcement learning, a subfield of machine learning (Sutton and Barto, 1998), has been successfully used to interpret the patterns of activity in dopaminergic areas during classical conditioning (Schultz, 1998). As dopamine modulates processing and learning in many brain areas, including the prefrontal cortex and the basal ganglia, this theoretical consideration has radically changed the interpretation of their role in various processes such as motor learning, action selection, working memory or decision-making. This analogy is still widely used by experimentalists and clinicians to interpret their observations, although several computational neuroscientists have since proposed more detailed and realistic neuro-computational models of the dopaminergic system (Brown et al., 1999; O’Reilly and Frank, 2006; Vitay and Hamker, 2014).
On the other hand, deep learning networks (LeCun et al., 2015) are directly derived from computational neuroscience research. The basic structure of a deep learning network for visual recognition is mapped onto the hierarchical organization of the visual cortex, with lower-levels areas extracting simple and local features from the retinal image (edges, gradients), and higher-level areas combining these lower features into complex shapes or even objects (Lecun et al., 1998). The most successful deep learning architectures make also use of sparseness as a regularization method to ensure an efficient coding of visual features, a concept which was first extensively studied by computational neuroscientists (Olshausen and Field, 1997; Spratling, 1999; Wiltschut and Hamker, 2009). Dropout, a regularization technique used to improve generalization in deep networks (Srivastava et al., 2014), is inspired from computational studies of stochastic synaptic transmission (Maass and Zador, 1999).
Challenges
Several issues are faced by computational neuroscience. The first one is the everlasting controversy on the adequate level of description to explain brain processes. Some models can be very detailed, using a model of the 3D morphology of specific neurons and a detailed description of chemical processes occurring inside the synapses. This bottom-up approach, exemplified by the Human Brain Project, relies heavily on data analysis to find the correct parameters and replicate observations. There is virtually no end to the degree of details that can be incorporated in such models. Despite its ambitious nature on this issue, one of the major criticisms addressed to HBP is that the level of description they chose will not be sufficient to capture all the properties of brain functioning. Contrary to physics or chemistry, neuroscience (including computational neuroscience) is non-paradigmatic in the sense of Thomas Kuhn (Kuhn, 1962): there is no common agreement inside the community on common axiomatic principles or models that could be used as a framework to interpret observations. Based on the enormous amount of unexplained experiments, the different schools of thought can select observations that fit into their paradigm and reject the ones that do not, leading to endless debates. Neuroscience is still in its infancy as a science, but the hope of defining a unified theory of brain functioning has to be maintained.
A more serious criticism to the bottom-up approach is that reproducing neural activity does not obligatorily mean to understand it. A complete simulated model of the brain, up to the last molecule involved, may end up as difficult to analyze and understand as an actual brain. What makes a human brain so special is not its number of neurons, nor its variety of cell types and neurotransmitters, but its different levels of organization: the complex and dynamical interaction between biological structures at different scales. The top-down approach to computational neuroscience starts from the behavioral function and breaks it iteratively into functional blocks that may eventually map onto the biological substrate. The corresponding models can be high-level mathematical descriptions, such as Bayesian inference (Doya et al., 2006), free-energy minimization (Friston, 2010) or optimization techniques (Sutton and Barto, 1998), while others use simplified neural models (spiking point-neurons, rate-coded neurons) to capture essential computational properties of neural networks. Top-down computational models obviously need to make strong assumptions about the underlying biological substrates and can only explain a limited range of observations. The whole difficulty is to define precisely enough the validity of the model: what can this model explain and predict, and where are its limits. For this kind of models, the key aspect is the ability to make predictions: they usually have enough degrees of freedom to fit virtually any set of experimental data, so their plausibility can only be evaluated by their predictive power.
A second problem faced by computational neuroscience is scalability. As neuro-computational models grow in size, the computational load to run the simulation becomes critical. The human brain comprises around 100 billions of neurons and tenths of trillions synapses. Even when using simple neural and synaptic models, the number of operations per second and the amount of memory needed by a complete brain model exceed the power of current supercomputers. The Human Brain Project has estimated that a complete brain model would require computational power at the exascale (one exaflops - 10^{18} - and 100 petabytes of memory) in order to function in real-time, while the fastest supercomputer at this date only proposes 50 petaflops (5 \cdot 10^{16}) of peak performance. The resulting simulation would consume 1.5 GW of energy if today’s architectures were simply scaled up (the goal is to reduce it to 20 MW by 2020), while the human brain merely requires 30W on average. On the short term, there is obviously a need for applying state-of-the-art parallel computing methods to the simulation of neuro-computational models. Several parallel neural simulators exist (NEST, GeNN, Brian, ANNarchy, etc) but they are usually limited to a particular type of neural models and on specific hardware platforms. On the longer term, one may need to rethink computer architectures: neural networks are inherently parallel, with localized processing units - the neurons - interacting through connections - the synapses - in continuous time. Simulating these networks on serial von Neumann architectures, even with many cores, is probably a waste of resources. Dedicated neuromorphic hardware solutions are being developed for the simulation of large-scale neural networks, for example the Spinnaker (Rast et al., 2011) and BrainScaleS (Fieres et al., 2008) projects, or the IBM SyNAPSE (Systems of Neuromorphic Adaptive Plastic Scalable Electronics) chip. They rely on fundamentally different concepts, such as asynchronous and event-driven computations, what leads to fast and energy-efficient simulations. However, these neuromorphic hardware platforms are not commonly available yet and require a strong programming effort.
Despite the different issues inherent to the youth of the field, computational neuroscience is a promising approach to artificial intelligence. It allows to bridge the gap between the quickly expanding knowledge on cognitive and emotional processes involved in behavior and the design of flexible and robust algorithms for intelligent behaving systems.
1.2 Motivated behavior
Animal behavior
Animal behavior can be decomposed into four categories: reflexes (low-level motor responses to stimuli which can not be voluntarily controlled), Pavlovian responses (the acquired association between a stimulus and an outcome, leading to conditioned responses), habits (more or less complex sequences of thoughts or actions which are routinely executed when triggered in a specific context) and goal-directed behavior (or motivated behavior, the ability to perform actions in order to achieve a particular goal) (Balleine and Dickinson, 1998). Pavlovian (or classical) conditioning is a passive learning process: an initially neutral stimulus (conditioned stimulus, CS) is repeatedly paired with a meaningful stimulus (unconditioned stimulus, US, which can be either positive - reward - or negative - punishment). The unconditioned response (UR) usually associated to the US becomes after a variable number of trials associated to the CS, becoming a conditioned response (CR). The classical experiment of Pavlov used a tone (CS) to predict the delivery of food (US) associated with drooling (CR). This form of conditioning does not require any action to be acquired, but can be used to adapt behavior by signaling the relevance of sensory events to higher-level functions. In appetitive conditioning, where the US is a food reward, the appearance of the CS prepares the animal to consumption, mainly through drooling but also possibly by interrupting the current behavior. In fear conditioning, where the US is a painful stimulation, the CS may trigger avoidance behaviors.
Oppositely, habits and goal-directed behavior are two components of instrumental (or operant) conditioning: the term covers all the processes which lead an animal to learn to produce actions in order to obtain rewards (positive reinforcers) or avoid punishments (negative reinforcers) (Skinner, 1938; Thorndike, 1911). While in Pavlovian conditioning the animal merely observes relationships in its environment, in operant conditioning it has control over the occurrence of reinforcers by adapting its behavior both during the learning phase and the exploitation phase. Operant conditioning is the key process in educating animals (for example teaching a dog new tricks by rewarding him after each successful action), but is also fundamental in free behavior: actions are directed toward the achievement of goals. Achieving a goal is a positive reinforcer for behavior, increasing the probability to achieve it again in the future, while failing to do so is a negative reinforcer which forces to adapt the current strategy or find a new one.
Although they are both directed toward goals, the difference between habits and goal-directed behavior is their dependency on the value of the goal. A classical experiment is the devaluation task: when the value of the reward is suddenly decreased (for example by inducing satiety before the experiment), goal-directed processes quickly avoid this outcome, while habitual behavior can persist for a long period of time (Balleine and Dickinson, 1998). Habits are therefore stimulus-response (S-R) mechanisms (a stimulus can trigger the behavior, even when the goal is not interesting anymore) while goal-directed processes are based on action-outcome (A-O) associations (which action do I need to perform to obtain this particular outcome?). The transfer of a goal-directed behavior to the habitual system is possible when the association is repeatedly experienced over an extended period of time. The mechanisms underlying this transfer are not yet fully understood, but they are thought to play an important role in the development of addiction (Everitt et al., 2001).
Explicit vs. implicit motivation
Goals can be extrinsically defined, for example when some food item is available in the environment. If the value of such a goal, possibly previously estimated through classical conditioning processes, exceeds sufficiently the costs associated to obtaining it, the animal engages in a series of actions that may lead to its obtainment, in which case these actions are reinforced. This form of operant conditioning is also called reinforcement learning, which is an important issue for both psychology and computer science. However, animals do not only produce actions which are directed toward primary reinforcers such as food, water or sexual partners: they play with their fellows or they explore their environment without any obvious reason for an external observer. The goals of such actions are called intrinsic rewards: satisfying one’s curiosity, checking if one’s beliefs are true, engaging in social interactions are as important from an evolutionary point of view as ensuring food supplies, reproduction or shelter (Barto et al., 2013; Kaplan and Oudeyer, 2007).
Extrinsic and intrinsic rewards are at the core of motivated behavior, as they determine the choice and intensity of motor plans to achieve them. Importantly, their value depends not only on the outcome itself, but also on its relevance for the organism: food items have an incentive (motivational) value only when the animal is hungry. This fact highlights the importance of embodiment, i.e. the fundamental link between the body and cognitive, emotional or motivational processes (Price et al., 2012). These processes are not ethereal as suggested by dualist theories of the mind but rather grounded in the body and aimed at ensuring its homeostasis (Cabanac, 1971; Damasio, 1994).
These fundamental properties of animal behavior, especially of human cognitive behavior, are still unaccessible to artificial systems. Current artificial systems mostly respond to specific stimuli by applying predefined or learned rules (stimulus-response associations). They are reactive structures which only seek new and relevant information when instructed to, not when they “want”, “need” or “like” it. There are only a few attempts to implement motivated behavior in such systems, e.g. intrinsic motivation on robotic platforms (Baldassarre et al., 2013; Mirolli et al., 2013), but they are still limited to toy problems. In order to build truly intelligent and autonomous artificial systems, fundamental properties such as intrinsic motivation and transfer of learning must be understood and formalized.
1.3 Reward and the dopaminergic system
Dopaminergic system
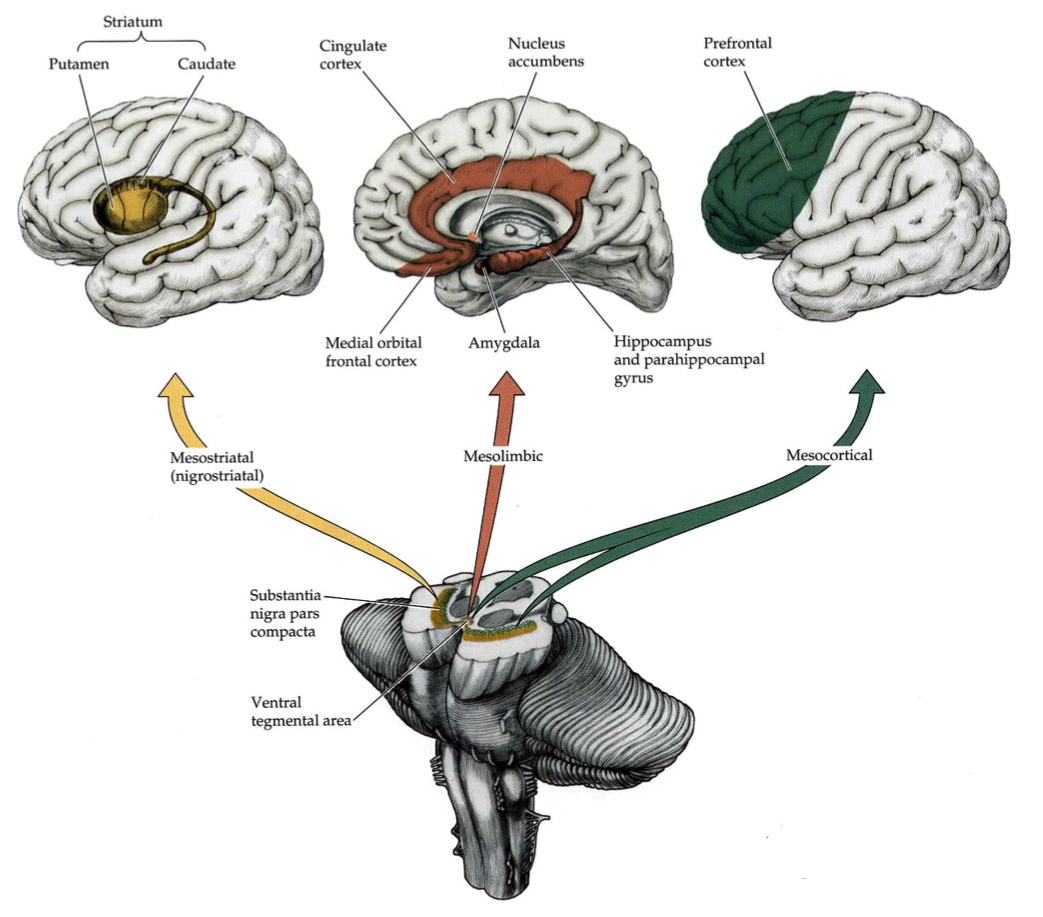
Dopamine (DA) is a key neurotransmitter in the brain. It is primarily produced by two small nuclei of the brainstem: the substantia nigra pars compacta (SNc) and the ventral tegmental area (VTA). Dopamine levels are involved in many processes such as the facilitation of approach behavior, incentive learning, motivation, novelty and saliency detection as well as reinforcement learning and action selection (Horvitz, 2000; Ikemoto, 2010; Sesack and Grace, 2010). As shown on Figure 1.1, dopaminergic neurons in SNc and VTA send projections along three different pathways: the nigrostriatal pathway comprises the projections between SNc and the basal ganglia (BG), especially its input structure the striatum. While SNc projects almost entirely to the BG, VTA projects both inside and outside the BG: the mesolimbic pathway reaches subcortical or phylogenetically ancient structures such as the nucleus accumbens (NAcc, also called ventral striatum in primates), the amygdala (a key area for emotional processing), the hippocampus (long-term memory formation and spatial navigation) and the cingulate cortex (error detection, self). VTA also projects diffusely to the cerebral cortex through the mesocortical pathway, reaching primarily the prefrontal cortex (PFC, planning, working memory), but also the motor cortex (movement) and the temporal lobe (visual processing and memory).
Neurons in VTA exhibit a rather low baseline activity (around 5 Hz) and become transiently active in response to various stimuli: novel and salient stimuli (Redgrave and Gurney, 2006), painful stimulations (Matsumoto and Hikosaka, 2009) and reward delivery (Ljungberg et al., 1992). Importantly, Schultz et al. (1997) showed an interesting characteristic of neural firing in VTA during classical appetitive conditioning in the primate. A visual conditioned stimulus (CS) is repeatedly paired with a food reward (US). At the beginning of learning, reward delivery generates a burst of activation of the VTA dopaminergic neurons (top of Figure 1.2), but not the appearance of the CS. After a few days of training, the pattern is reversed (middle of Figure 1.2): the appearance of the CS provokes a DA burst, but not reward delivery anymore. Moreover, when the reward delivery is predicted by the CS but omitted (bottom of Figure 1.2), DA cells show a pause in firing (a dip) at the time reward is expected.
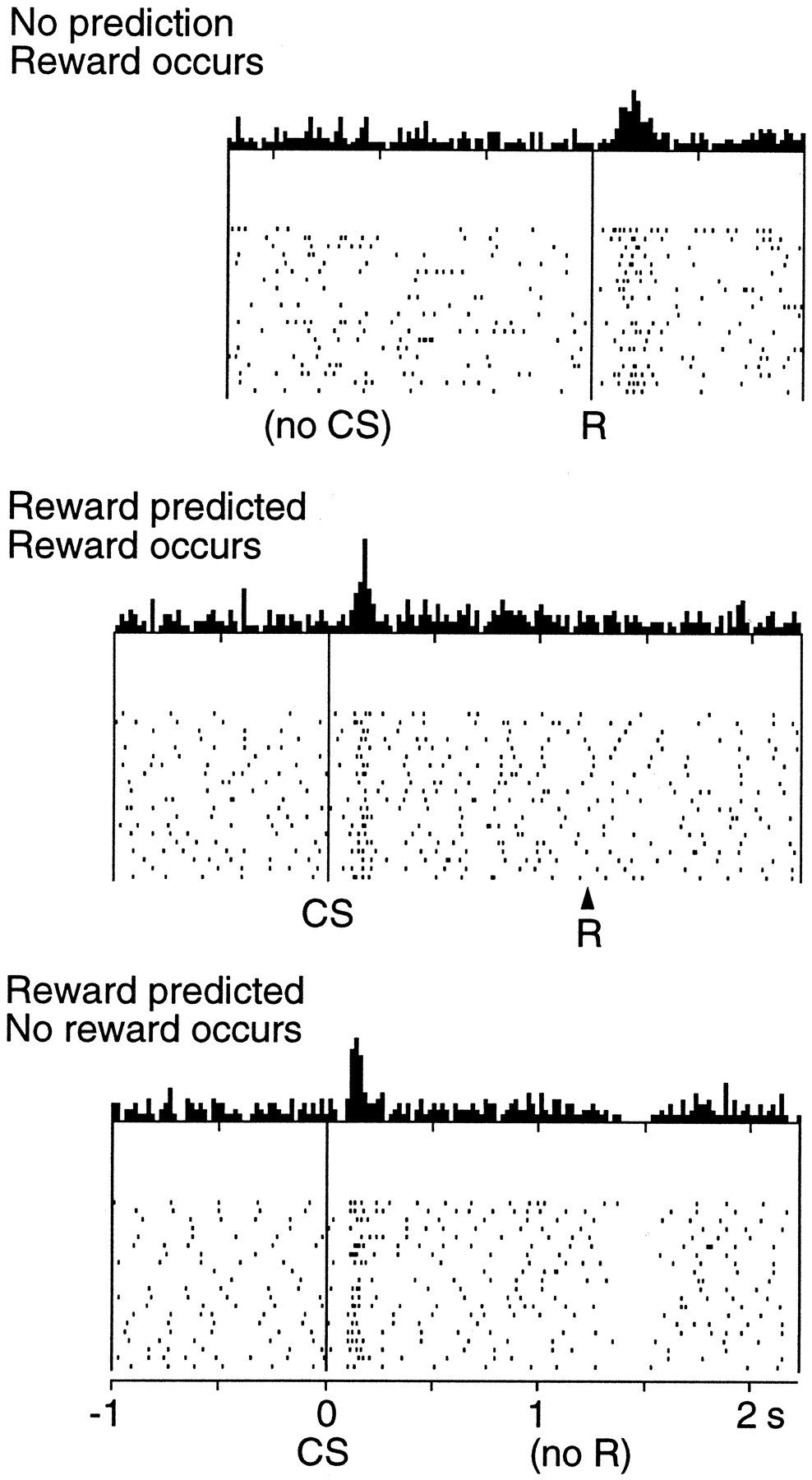
This pattern of activation suggests that VTA cells collectively encode a reward prediction error (RPE), defined as the difference between the reward actually received and the predicted reward. If more reward is received than expected, the RPE is positive, which happens when reward delivery is unexpected (not - yet - predicted) or when a CS appears (the appearance of the CS itself is unpredictable, but it signals that reward will be delivered). If less reward is received than expected, the RPE is negative, corresponding to the dip in VTA activity when reward is omitted. If reward is received as expected, the error is equal to zero. This happens when the CS fully predicts reward delivery.
TD analogy
An analogy between this RPE pattern of VTA cells during conditioning and the temporal difference (TD) algorithm of reinforcement learning (Sutton and Barto, 1998) became quickly dominant. In the reinforcement learning framework, each state s of a finite Markovian Decision Process (MDP) is associated with a value function V^\pi (s) which represents the expectation of the sum of rewards that will be obtained after being in the state s and thereafter following a policy \pi:
V^{\pi} (s) = E_{\pi} ( R_t | s_t = s) = E_{\pi} ( \sum_{k=0}^{\infty} \gamma^k r_{t+k+1} | s_t = s )
\gamma is a discounting factor allowing to scale the relative importance of immediate rewards (which will be obtained shortly after being in the state s at time t) compared to rewards obtained on the longer term. In the TD algorithm, the value of a state is estimated iteratively after each transition between a state s_t and a state s_{t+1}:
V^{\pi}(s_t) \leftarrow V^{\pi}(s_t) + \alpha \cdot (r_{t+1} + \gamma\cdot V^{\pi}(s_{t+1}) - V^{\pi}(s_t) )
The TD error signal:
\delta_t = R_t - V^{\pi}(s_t) = (r_{t+1} + \gamma\cdot V^{\pi}(s_{t+1}) ) - V^{\pi}(s_t)
is a reward prediction error signal, as it compares the rewards actually received after the state s_t with their prediction V^{\pi}(s_t). More precisely, the rewards actually received are decomposed into the reward immediately obtained during the transition (r_{t+1}) and an estimation of the rewards that will be obtained after being in s_{t+1} (V^{\pi}(s_{t+1}), discounted by \gamma). When more reward is obtained than predicted (either because the immediate reward r_{t+1} is high, or because the transition leads to a state with a high value), the RPE signal is positive and increases the value of the state. If less reward is received than expected, the TD error signal is negative and decreases the value of the state.
To account for classical conditioning, states have to represent discrete time events. As by definition no action is required to obtain the rewards, transitions between states occur on a fixed schedule. At the beginning of conditioning, all states are initialized with a value of 0. The first time a reward is delivered, the TD error becomes positive for the preceding state: it was not predicting any reward but one occurred. At the next trial, if the reward arrives at the same time, its value will be slightly higher, so the TD error will be smaller. Meanwhile, the preceding state will see its value increased, because it leads to a state with a positive value. After several conditioning trials, the value of all states preceding reward delivery will be positive. The TD error is zero for the transitions between theses states, as they correctly predict reward delivery. Only the transition to the state corresponding to the appearance of the CS will have a positive TD error signal: the system was in a state where no reward is predicted (the animal is waiting for something to happen) but the transition leads to a state where reward will be delivered after a certain delay. If the reward is not delivered during the usual transition, the TD error becomes negative.
However, over the course of learning multiple trials, the positive TD error signal “travels” back in time, peaking first at reward delivery, then at the preceding state, until it appears at CS onset. In order to fully account for the observations of Schultz et al. (1997), where reward-related activation of VTA cells slowly decreases with learning while the CS-related one increases, but nothing happens in-between, one has to use a modified version of the TD algorithm called TD(\lambda) (Sutton, 1988). In this variant, when a reward is delivered, not only the value of the preceding state is updated, but also all the preceding states, with a magnitude weighted by the decreasing series \lambda^{t-k}. Consequently, the state corresponding to CS onset gets also updated the first time reward is delivered. When \lambda is chosen close enough to 1, the resulting pattern of activation of the TD error signal matches the experimental observations on VTA firing (Schultz, 1998).
Alternative models
This striking analogy was immediately successful and led to many top-down models of the role of DA in both classical and operant conditioning (Daw and Touretzky, 2002; Rao, 2010; Samejima and Doya, 2007; Smith et al., 2006; e.g. Suri and Schultz, 2001). There are however many aspects of DA firing in VTA which are not explained by the TD analogy. When reward is delivered earlier than predicted, VTA cells are activated at reward delivery but stay at baseline at the usual time (Hollerman and Schultz, 1998), contrary to what is predicted by TD. When reward delivery is uncertain, dopaminergic neurons first respond phasically to CS onset and then increase their activity until reward delivery with a slope depending on its probability (Fiorillo et al., 2003). Moreover, DA neurons also respond to novel and salient stimuli which are not predictive of reward (Redgrave and Gurney, 2006).
The main problem is the way time is represented: transitions between states are supposed to occur at a fixed rate, determined by some internal clock. A TD model is only able to learn a single CS-US interval with a constant duration. However, classical conditioning is robust to variability in the CS-US interval (Kirkpatrick and Church, 2000). Many models have been proposed to improve the representation of time in TD models, including serial-compound representations (Suri and Schultz, 2001) and Long Short-Term Memory networks (LSTM, Rivest et al., 2010). More sophisticated neuro-computational models separate the mechanisms responsible for CS-related and US-related activations (Dranias et al., 2008; O’Reilly and Frank, 2006; Vitay and Hamker, 2014). Based on the neuroanatomy of the afferents to the dopaminergic system, they distinguish the sources of excitation and inhibition signaling reward delivery to VTA from the ones signaling predictors of rewards. In Chapter 5, we will discuss these models and explain their importance for motivated behavior.
Despite these limitations, it is clear that DA firing in VTA represents a RPE that can be used to reinforce actions or plans in other structures such as the BG or the prefrontal cortex. However, if the amount of evidence for the role of positive RPEs is undebatable, it is still unclear what is the effect of negative RPEs, for example when a predicted reward is omitted. VTA cells fire at a rather low baseline activity (5 Hz) and the mechanisms by which a pause in firing can influence plasticity in efferent systems are still a matter of debate (see Shen et al., 2008 for an explanation on its role in the striatum). Moreover, the observed dip in VTA activity when reward is omitted has not been reproduced by other researchers (Joshua et al., 2009). Many efforts remain to be done to fully understand how VTA and SNc signal reward-prediction errors to the BG and prefrontal cortex. VTA is for example known to send also inhibitory projections to the ventral striatum (Brown et al., 2012), what opens new questions on the exact role of VTA in reward processing (Creed et al., 2014).
1.4 Basal ganglia and reinforcement learning
Anatomy
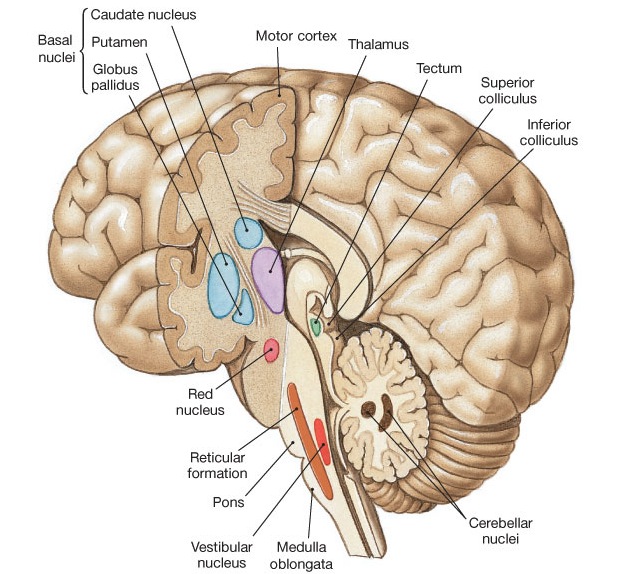
The basal ganglia are a set of nuclei in the basal forebrain (Figure 1.3). They receive inputs from the entirety of the cerebral cortex (although the frontal lobe is dominant) and project to various sub-cortical nuclei such as the brainstem or the thalamus, where the processed information can go back to the cerebral cortex. They are involved in a variety of functions, among which the control of voluntary movements, action selection, sequence learning, habit formation, updating of working memory (WM), motivation and emotion. Their importance for behavior is emphasized by their involvement in many neurological diseases, including Parkinson’s disease, Huntington’s disease, Tourette syndrome, obsessive-compulsive disorders, addiction and schizophrenia.
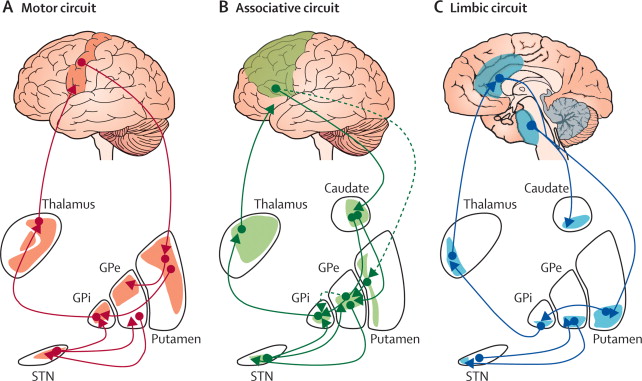
The striatum (STR) is the main input structure of the BG. In the primate, it is composed of the dorsal striatum (caudate nucleus - CN - and putamen - PUT) and the ventral striatum (nucleus accumbens - NAcc - and olfactory tubercle). It receives massive inputs from the whole cerebral cortex, with the ventral striatum also receiving inputs from sub-cortical structures such as the hippocampus or the amygdala (Humphries and Prescott, 2010). It is principally composed of medium spiny neurons (MSNs) which are able to integrate cortical inputs from different areas and project inhibitorily inside the BG on the globus pallidus (GP). Two types of MSNs are found in the striatum depending on the dopamine receptors they exhibit: D1-mediated and D2-mediated MSNs. They contribute to different pathways within the BG depending on the part of the GP they project on: its internal part (GPi) for D1 MSNS, the external one (GPe) for D2 MSNs. The second input structure of the BG is the subthalamic nucleus (STN). Although much smaller, it also receives massive cortical inputs and projects excitatorily on the GP.
The output structures of the BG are GPi and the substantia nigra pars reticulata (SNr). As they are functionally similar, they are often labeled together as GPi/SNr, although they are not anatomically close. Neurons in GPi/SNr are tonically active, meaning that they have an elevated firing rate baseline (between 60 and 80 Hz). At rest, they exert a strong inhibition on target structures of the BG, including the thalamus. GPi/SNr must be themselves inhibited in order to release this inhibition and allow the target structures to get activated, a phenomenon called disinhibition (Chevalier and Deniau, 1990). As a whole, the BG act as a gating regulator of activity in target structures.
Pathways
The internal connectivity of the BG shows a complex organization (Figure 1.4). Three principal pathways can nevertheless be identified. The direct pathway goes directly from D1-mediated MSNs to GPi/SNr. It is the main source of disinhibition for the output of the BG. The indirect pathway originates in the D2-mediated MSNs and relays in GPe before targeting GPi/SNr either directly or through STN. The additional inhibitory relay on GPe makes this pathway globally excitatory on GPi/SNr: the activation of D2-mediated MSNs increases firing rates in GPi/SNr, what further prevents target structures to get activated. The opposing effects of the direct and indirect pathways led to the first models of motor processing in the BG (Albin et al., 1989; DeLong, 1990). The balance between their opposing effects (“Go” for the direct pathway, “No Go” for the indirect one) allows to control the initiation, vigor and termination of motor movements. Pathological imbalance between the pathways can explain neurological diseases: dopamine loss, characteristic of Parkinson’s disease (PD), weakens the direct pathway, as DA has an excitatory effect on D1-mediated MSNs and inhibitory on D2-mediated ones (Gerfen et al., 1990; Surmeier et al., 2007). The resulting increased inhibition on motor centers causes hypokinesia, the inability to initiate movements. On the contrary, excess of dopamine, as in Huntington’s disease (Chen et al., 2013) or Tourette syndrome (Albin and Mink, 2006), over-activates the direct pathway and leads to hyperkinetic symptoms, such as involuntary movements and tics.
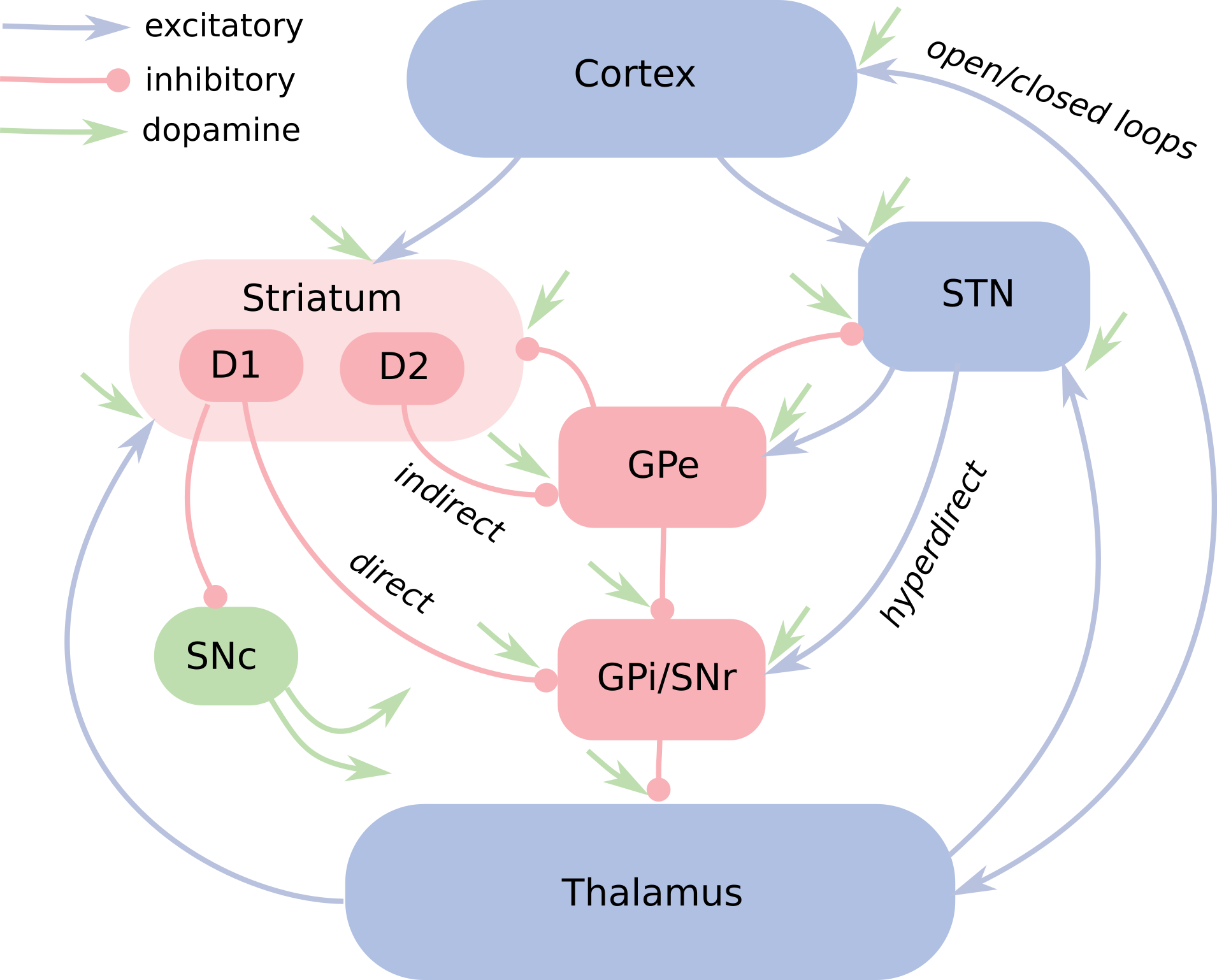
The hyperdirect pathway connects directly STN to GPi/SNr through excitatory synapses, with a much lower latency than the other pathways (Nambu et al., 2002). It allows to send rapidly cortical information to the output nuclei of the BG, bypassing computations in the direct and indirect pathways. Because of its excitatory effect on GPi/SNr and the diffuse projection of SNr on GPi/SNr (a neuron in STN excites many neurons in GPi/SNr), it carries a “Global No Go” signal allowing to suppress involuntary movements or to terminate them prematurely. According to Nambu et al. (2002), the three pathways may cooperate during action selection following a center-surround model: when a voluntary movement is initiated by cortical areas, the hyperdirect pathway first inhibits large areas of the thalamus and cerebral cortex that are related to both the selected movement and its competitors. For example, before moving the arm to the left, any arm movement previously prepared will be wiped out by the increased excitation in GPi/SNr. Some milliseconds later, the direct pathway selects the appropriate motor program while the indirect pathway selectively inhibits competing movements.
These three pathways form a classical feedforward view of the BG which has been used in many models (Gurney et al., 2001; O’Reilly and Frank, 2006; Schroll et al., 2012). As depicted in Figure 1.4, there exists many other projections inside the BG which render the understanding of processing within the BG much more complex. The thalamostriatal pathway, formed by projections from the thalamus to the striatum, may for example be involved in attentional processes and help the BG solve the credit-assignment problem (Galvan and Smith, 2011). The reciprocal connections between STN and GPe lead to oscillations under certain circumstances, what could form the basis of an internal pacemaker inside the BG (Plenz and Kital, 1999), but can also become pathological in Parkinson’s disease and explain symptoms such as tremor (Levy et al., 2002). Much remains to be done to fully understand the role of the STN-GPe loop (Kumar et al., 2011). The role of the pallidostriatal projection between GPe and the striatum is also still mainly unexplored (Bahuguna et al., 2015; Kita et al., 1999).
Dopamine-mediated plasticity
The striking feature of the BG is their dependency on dopamine, either as a modulator of activity - elevated DA levels increase the excitability of D1-mediated MSNs and decrease the one of D2 cells (Nicola et al., 2000) - or of plasticity - different DA levels can induce selectively long-term potentiation (LTP) or long-term depression (LTD) at corticostriatal synapses (Calabresi et al., 2007). All nuclei of the dorsal BG receive dopaminergic input from SNc, while the ventral part receives mainly inputs from VTA. Reciprocally, the striatum is a major source of inhibition to the dopaminergic areas, allowing the BG to control their own dopaminergic input (Haber et al., 2000).
Dopamine-mediated plasticity is particularly studied in the striatum. MSNs exhibit particular dynamics: their membrane potential can be either in a hyperpolarized down-state or in a depolarized up-state. In the down-state, the excitability of the cell is very low and striatal neurons do not emit spikes. In the up-state, the cell is very excitable and responds to its cortical inputs. The transition between these two states can be spontaneous (it occurs at a rate of 0.5 to 2 Hz, Leung and Yim, 1993), induced by a phasic DA burst in VTA/SNc (Gruber et al., 2003) or by a massive cortical input (McGinty and Grace, 2009). For D1-mediated MSNs, LTP is known to occur at corticostriatal synapses in the presence of a strong cortical input and under elevated DA levels when the cell is in the up-state. LTD happens on the contrary when there are weak cortical inputs, low DA levels and the cell is in the down-state (Calabresi et al., 2007; Reynolds and Wickens, 2000). Put together, plasticity at corticostriatal synapses seems to be driven by a three-term DA-modulated Hebbian learning rule, where the change in synaptic efficiency is ruled by the product of the pre-synaptic activity (r^{\text{pre}}, presence of cortical inputs), the post-synaptic activity (r^{\text{post}}, up- or down-state) and the deviation of the dopamine level from its baseline \delta:
\Delta w = \delta \cdot r^{\text{pre}} \cdot r^{\text{post}}
The opposite pattern is found for D2-mediated MSNs: high DA levels induce LTD while low levels induce LTP (Shen et al., 2008). With this model of corticostriatal plasticity, DA becomes able to selectively reinforce corticostriatal associations. If a motor plan selected by the direct pathway led to reward, DA will strengthen the corticostriatal synapses to D1-mediated MSNs that were previously activated and reduce the ones to D2-mediated MSNs. This increases the probability that the same motor plan will be selected again in the future by favoring the direct pathway in its competition with the indirect one. Oppositely, if the action leads to less reward than expected, the D1-mediated synapses will be reduced and the D2-mediated ones increased, what strengthens the indirect pathway and prevents further selection of that motor plan.
This mechanism of dopamine-based reinforcement in the BG further emphasized the analogy with reinforcement learning, especially the actor-critic architecture (Sutton and Barto, 1998). In this framework, the critic produces the TD error signal which is used both to update the value of a state and to reinforce the state-action association that led to reward. Using this error signal, the actor simply learns to map a state onto the optimal action. In this view, the critic would be composed by the dopaminergic system and the ventral BG, while the actor represents a loop between the cerebral cortex and the dorsal BG. Many neuro-computational models of the BG are based on this architecture (Berns and Sejnowski, 1998; Gurney et al., 2001; Houk et al., 1995; Joel et al., 2002).
Many criticisms have been formulated to this model. First, DA cells do not only signal RPEs but also respond to aversive, salient and novel stimuli, which does not fit into the reward-prediction error hypothesis (Pennartz, 1995). They also respond to reward-predicting stimuli with a very short latency, raising the issue of how their reward-predicting value can be predicted in such a short time (Redgrave et al., 1999). DA is even not required for acquiring the value of a stimulus (“liking”), only for its motivational effect (“wanting”), so the role of the critic might be misunderstood (Berridge, 2007). Another issue with the actor-critic assumption is the temporal credit-assignment problem: rewards are usually delivered well after the causal action is executed. How can this delayed feedback influence motor representations which have long faded away?
More detailed neuro-computational models have been introduced to overcome these issues. The PBWM (prefrontal cortex, basal ganglia working memory) model of O’Reilly and Frank (2006) makes a strong use of working memory (WM) processes to bridge the temporal gap between an action and its consequences. It furthermore provides a mechanism by which the content of WM is gated and updated by functional loops between the PFC and the BG. A similar approach was taken in Vitay and Hamker (2010), which will be presented in Chapter 3. This model was the first to consider the importance of plasticity within the BG (specifically in the projections from the striatum to the globus pallidus) in addition to corticostriatal plasticity.
Generally, the role of the BG in motor learning and action selection is partially understood, but its contribution to other forms of learning has been less extensively studied. An interesting view considers the BG as a fast learning device quickly acquiring rewarded associations and transferring them to the cerebral cortex where they will be generalized and stored in long-term memory (Ashby et al., 2005). This hypothesis is backed up by the well-accepted role of the BG in habit formation (Seger and Spiering, 2011). Even more generally, one can consider the BG as a trainer for the cerebral cortex. Learning in the cerebral cortex can be characterized as unsupervised, in the sense that cortical neurons self-organize to represent internal and external events in the most efficient way. Cortical areas communicate with and adapt to each other, but there is no obvious objective function guiding the learning process (supervised learning minimizes an error function, which is unavailable at the cortical level), while reinforcement learning has to be ruled out because of the slow temporal dynamics of dopamine in the cortex (the bursts and dips of the DA signal are too smoothed out in the cortex to carry the RPE, Seamans and Yang, 2004). The role of BG would be to transfer specific knowledge acquired by reinforcement learning to the more general unsupervised cortical system. In the view of Stocco et al. (2010), the BG may also act as a conditional information-routing system, enabling transmission between remote cortical areas and allowing the learning of new associations.
1.5 Multiple loops and organization of behavior
It was mentioned that the striatum receives projections from the entirety of the cerebral cortex. However, the organization of these projections follows a specific topology on the surface of the striatum. As depicted in Figure 1.5, different cortical regions project onto different parts of the striatum: the motor and premotor (PMC) cortices project mainly onto the putamen, the dorsolateral prefrontal cortex (dlPFC) projects mainly on the caudate nucleus, while the orbitofrontal (OFC) and ventromedial prefrontal (vmPFC) cortices project mainly on the nucleus accumbens. As this segregation is preserved throughout the BG, from the projections of the striatum on the GP to the thalamic nuclei relaying the output of the BG back to the cortex, the prefrontal cortex / basal ganglia system is said to be organized in parallel segregated loops (Alexander et al., 1986).
Each loop is therefore specialized in a particular functional domain: the motor loop is involved in motor learning and action selection, the associative loop in cognitive processes such as sequence learning and WM updating, the limbic loop in motivation and goal-directed learning. These subdivisions can be further refined: the motor loop is in fact composed of multiple segregated loops depending on the cortical region of origin (M1, SMA, pre-SMA…). Other loops have been identified, such as the oculomotor loop, devoted to the control of eye movements, or the visual loop, linking the inferotemporal and medial temporal cortices to the tail of the caudate nucleus. The importance of the visual loop will be explained in Chapter 2 and Chapter 3. A similar topological segregation can further be extended to the projections within a functional loop: the topology of the cortical area (e.g. the somatotopic representation of body parts in the motor cortex) is preserved inside the BG (Nambu, 2011). In this view, the PFC/BG system is composed by thousands of small parallel loops (O’Reilly and Frank, 2006).
The segregation is however not total: a certain degree of overlap is observed in the corticostriatal projections, allowing for example parts of the striatum to integrate both motor and associative information. The funneling structure of the BG - there are 100 times more neurons in the striatum than in GPi/SNr - also increases the probability that the loops communicate with each other inside the BG (Bar-Gad et al., 2003). Finally, the thalamic nuclei relaying the output of the BG back to the cortex do not target only the original cortical area, but reach also adjacent ones. In the PFC / BG system, one distinguishes closed loops, where a single cortical area projects to the striatum and receives the processed information back, from open loops, where a cortical area sends information to the BG and the result is “forwarded” to another cortical area (Ebner et al., 2015). Category learning in the visual loop between the inferotemporal cortex and the BG is for example transferred to the motor cortex through an open loop (Seger, 2008). The exact organization of the PFC / BG system into closed and open loops is still not precisely known, but this is an important mechanism by which the BG can modulate information transmission in the prefrontal cortex (Stocco et al., 2010).
The question that arises is how these multiple loops could learn useful associations in their respective domains based on a single unitary reward-prediction error signal, as hypothesized by the TD analogy. SNc and VTA actually display a complex topological organization depending on their reciprocal connections with the striatum (striato-nigro-striatal system, Haber et al., 2000). As depicted in Figure 1.6, each region of the striatum engaged in a closed loop with the cerebral cortex forms reciprocal connections with a specific region of the SNc/VTA dopaminergic areas: the striatum sends inhibitory connections to SNc/VTA, which returns a dopaminergic signal. However, each striatal region also projects on the adjacent dopaminergic region along a rostro-caudal axis, i.e. from limbic to associative to motor domains. This pattern on connectivity forms a spiraling structure which allows different striatal regions to influence others by modulating their dopaminergic inputs.
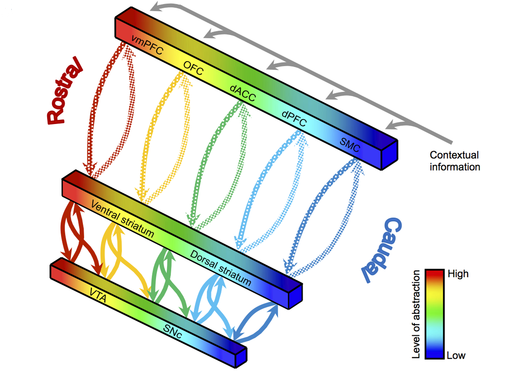
The resulting organization of PFC-BG loops along a limbic-associative-motor gradient has fundamental consequences on goal-directed behavior. Limbic regions, critical for motivational and affective processes, are in a position to influence how cognitive plans are formed and learned by associative regions, which themselves control how individual movements and actions are executed in motor regions. This highlights the tight integration between cognitive and emotional processes: goals are mainly represented in OFC, which is strongly connected with the limbic system (amygdala, ventral BG) and influences cognitive processes in dlPFC. Based on neuro-anatomical evidence, the classical view opposing cognition and emotion as competitors to produce behavior has to be replaced by an emphasis on the cooperation between the two systems.
This gradient also has consequences on learning: striatal regions associated to goal-directed learning influence plasticity in striatal regions associated to habit formation (Khamassi and Humphries, 2012; Yin et al., 2004). This provides a mechanism by which flexible behaviors acquired through goal-directed learning can be transferred into procedural memory to become habits. Similarly, Pavlovian-to-Instrumental transfer (PIT) is the ability to transfer stimulus values acquired through Pavlovian conditioning to instrumental behavior: after a first phase of operant conditioning where a rat learns to press levers to obtain different outcomes (say, food and water), a classical conditioning phase is introduced, pairing initially neutral stimuli (tone or light) to the same outcomes. The effect of PIT is that, when back in the operant conditioning room, the conditioned stimuli will now trigger the lever press leading to the same outcome (Corbit and Balleine, 2011). The mechanisms allowing a transfer of learning between classical and instrumental conditioning happen in the cooperation between two loops within the ventral BG, involving two parts of the nucleus accumbens, the core and the shell (Gruber and McDonald, 2012).
Although the concept of multiple parallel PFC/BG loops has been often used in neuro-computational models (N’guyen et al., 2014; e.g. Nakahara et al., 2001; O’Reilly and Frank, 2006), only a few have used the underlying limbic-associative-motor gradient in dopaminergic connectivity to investigate the organization of behavior. Keramati and Gutkin (2013) for example studied this system to explain the mechanisms of addiction. In Schroll et al. (2012) (Chapter 4), we proposed a neuro-computational model of working memory formation and maintenance involving three PFC/BG loops, two associative and one motor, which coordinate their learning through the spiraling striato-nigro-striatal system. The dopaminergic system has a central role in organizing behavior and learning; very simplified models such as TD actually limit our ability to understand the underlying processes.
1.6 Structure of the thesis and contribution
This thesis is composed of five articles published in international peer-reviewed journals. They were selected to be representative of the different aspects of my research on the role of dopamine in motivated behavior. In Vitay and Hamker (2008) (Chapter 2), we studied the influence of dopamine on memory retrieval in the perirhinal cortex, a part of the temporal lobe involved in object recognition and visual memory. In Vitay and Hamker (2010) (Chapter 3), we designed a neuro-computational mode of the BG which is able to solve delayed rewarded visual memory tasks. This fundamental model was the first to introduce plasticity within the BG and was further extended in collaboration with Dr. Henning Schroll to account for working memory formation Chapter 3. In Vitay and Hamker (2014) (Chapter 5), we designed a detailed model of the dopaminergic system during conditioning, with a strong emphasis on its dependency on timing processes. Additionally, in Vitay et al. (2015) (Chapter 6), we present a neural simulator that was developed in parallel and which allows to define these neuro-computational models easily and simulate them efficiently on parallel hardware. A detailed description of the content of these articles is provided in the following sections.
List of publications included in the thesis
Vitay, J. and Hamker, F. H. (2008). Sustained activities and retrieval in a computational model of the perirhinal cortex. Journal of Cognitive Neuroscience, 20, 11, 1993-2005, doi: 10.1162/jocn.2008.20147
Vitay, J. and Hamker, F. H. (2010). A computational model of basal ganglia and its role in memory retrieval in rewarded visual memory tasks. Frontiers in Computational Neuroscience, 4, doi: 10.3389/fncom.2010.00013
Schroll, H., Vitay, J., and Hamker, F. H. (2012). Working memory and response selection: a computational account of interactions among cortico-basalganglio-thalamic loops. Neural Networks, 26, 59–74, doi: 10.1016/j.neunet.2011.10.008
Vitay, J. and Hamker, F. H. (2014). Timing and expectation of reward: a neuro-computational model of the afferents to the ventral tegmental area. Frontiers in Neurorobotics, 8, 4, doi: 10.3389/fnbot.2014.00004
Vitay, J., Dinkelbach, H. Ü., and Hamker, F. H. (2015). ANNarchy: a code generation approach to neural simulations on parallel hardware. Frontiers in Neuroinformatics, 9, 19, doi:10.3389/fninf.2015.00019
Contribution to each article
I am the primary author of articles 1, 2 and 4, having conducted the research, implemented the models, performed the experiments, analyzed the results and primarily written the manuscripts. Prof. Hamker supervised the research, guided the whole process and participated in the writing. For article 3, Dr. Henning Schroll is the primary author. He implemented the model, ran the experiments, analyzed the results and primarily wrote the article. I co-supervised the development of the model together with Prof. Hamker and participated in the writing. For article 5, Helge Ülo Dinkelbach was involved in developing the neural simulator and running the experiments, co-supervised by Prof. Hamker and me. I developed equally the neural simulator and wrote primarily the manuscript.
1.6.1 Chapter 2 : Perirhinal cortex and dopamine
Working memory is the ability to temporarily store and manage information in order to use it for cognitive processes (Baddeley, 1986). A typical example is remembering a phone number before typing it: the number is stored in short-term memory as long as it is needed for the action, but the memory fades away when it is not required anymore. The neural correlate of WM processes is sustained activation: neurons which are activated by the presence of the information stay active during the whole period between its disappearance and its later use by cognitive processes. Sustained activation has been found in many brain areas, including the prefrontal cortex (Funahashi et al., 1989), the parietal cortex (Koch and Fuster, 1989), the inferotemporal cortex (Ranganath et al., 2004) and the medial temporal lobe (Naya et al., 2003). The medial temporal lobe (MTL) has an important role in interfacing high-level visual information represented in the inferotemporal cortex (IT) with long-term mnemonic information encoded in the hippocampal formation. It is composed of the perirhinal (PRh), entorhinal (ERh) and parahippocampal (PHC) cortices.
PRh is in particular involved in visual object categorization (Murray and Richmond, 2001), multimodal integration (Taylor et al., 2006), long-term memory encoding (Buffalo et al., 2000) and retrieval (Brown and Xiang, 1998). In visual object categorization, PRh develops view-independent representation of objects: objects are in general seen from particular angles or are only partially visible. PRh learns to integrate over time these different views and bind them together in a unitary representation. In the model of PRh we developed (Vitay and Hamker, 2008), PRh is represented by two populations of excitatory and inhibitory neurons, respectively, with biologically plausible proportions and connectivity. Different objects are presented to the model through connections from a model of IT to the excitatory neurons. Each object is composed of different parts, which are randomly selected at each presentation: for example the first presentation of a chair would contain its right side and three feet, the second would be its back and only two feet, and so on. Through plasticity in the lateral connections between the excitatory neurons, we observe the formation of connected clusters of neurons which represent the object as whole: individual neurons of the cluster receive visual input from only one part of the object, but they have become connected to neurons representing all the other parts of the object.
Sustained activation has been observed in PRh during delayed matching-to-sample (DMS) tasks, where a visual object (the sample) is shortly presented and removed for a variable duration called the delay period. The same or a different object (the match) is then presented and the subject has to respond if the new object matches the sample. PRh neurons representing the sample object stay active during the delay period (Nakamura and Kubota, 1995). The model reproduces this effect by incorporating the effect of DA on synaptic transmission in the cortex, extrapolated from its known influence in the prefrontal cortex (Durstewitz et al., 2000; Seamans and Yang, 2004). We observed that PRh neurons show sustained activation under intermediate levels of DA, but not low or high doses, a phenomenon known as inverted-U curve in the prefrontal cortex (Vijayraghavan et al., 2007). Moreover, intermediate levels of DA favor the propagation of activity within a cluster: while at low DA levels only the neurons receiving visual information get activated, the whole cluster gets activated at intermediate levels because of the enhanced lateral connections within the cluster. Instead of representing a partial view of the object, PRh represents all possible views at the same time, leading to a complete representation of the object. This provides a mechanism by which DA modulates processing in PRh and allows memory retrieval.
The mechanisms used in this model are a very important step for visual processing as they allow view-invariant representations of an object to be formed and retrieved by cognitive processes. Under optimal DA levels, object representations can be completed and help categorization. Furthermore, the visual template representing an object in PRh can be activated by cognitive processes (either through direct projections from the PFC or through the thalamus) and used to guide visual search. The visual system is principally organized in two separate pathways: the ventral pathway, originating in the primary visual cortex (V1) and ending in the inferotemporal lobe, is specialized in object recognition; the dorsal pathway, originating in V1 and ending in the parietal cortex, focuses on the localization of visual objects and their manipulation (Ungerleider and Mishkin, 1982). Activating a template in PRh biases IT toward the characteristic features of this object, which itself biases representations in the ventral pathway through feedback projections. Once the corresponding features are enhanced in V1, the dorsal pathway can then locate the object and direct an action toward it (Hamker, 2004; Hamker, 2005). Understanding how visual templates are formed and retrieved is a first step toward understanding the cognitive control of vision.
Insights on the role of DA
Tonic levels of DA control the processing properties of PRh by switching from a representational mode - only the perceived information is represented - to a mnemonic one - visual templates are completed or retrieved.
1.6.2 Chapter 3 : Basal ganglia and memory retrieval
Maintaining visual templates in PRh is a critical component of delayed rewarded tasks such as delayed match-to-sample (DMS, reward is delivered if a response is made when the target matches the sample), delayed non-match-to-sample (DNMS, the response is rewarded only if the target does not match the sample) or delayed pair-association (DPA, similar to DMS but there is a an arbitrary association between the sample and the rewarded target - e.g. respond for an apple when the sample is a car). The visual loop of the BG, linking high-level visual cortical areas such as IT and PRh with the body and tail of the caudate nucleus, is involved in selectively activating visual templates during the delay period of such tasks in order to prepare the correct response (Levy et al., 1997). The major difficulty of these three tasks is that the visual template to be activated can be different from the presented sample, so the target has to be retrieved from memory.
In Vitay and Hamker (2010), we developed a neuro-computational model of the visual loop of the BG. It is composed of a closed loop between PRh, the caudate nucleus, SNr and the ventro-anterior thalamus, and an open loop with a projection from the dlPFC to the caudate nucleus. Contrary to the generic scheme described on Figure 1.4, we only modeled the direct pathway of this loop. In the experimental setup, a sample is first presented and stored in dlPFC. After a delay of 150 ms, a cue indicated which task to perform (DMS, DNMS or DPA) is presented and stored in dlPFC. Finally, after another delay, two stimuli are presented: the target (which matches the sample depending on the task) and a distractor. After a delay, we measure the maximal activity in PRh and deliver reward to SNc if the target has a higher activity. The dopaminergic signal in SNc in response to the reward modulates learning at corticostriatal synapses (both from PRh and dlPFC) according to the three-term DA-modulated Hebbian learning rule presented in this chapter. This is in line with many models of the BG (e.g. Brown et al., 1999; O’Reilly and Frank, 2006). The novelty of this model is that DA also modulates plasticity within the BG, in the connections from the striatum to SNr as well as in the lateral connections of SNr.
This internal plasticity, confirmed by experimental evidence (Rueda-Orozco et al., 2009), releases the constraints on the striatum. In other models, each striatal region converges on a small number of GPi/SNr cells, allowing to disinhibit a single action. The corticostriatal projections must therefore solve two different problems: integrating different cortical representations (here, the sample and the task cue) and map them on the correct action. If plasticity in the projection between the striatum and GPi/SNr is added, corticostriatal projections only need to map cortical associations on the striatum (a form of self-organization), while the striatopallidal ones learn to map these representations onto the correct action. Additionally, plasticity within SNr ensures selectiveness in the output of the BG.
The resulting model is able to learn through reinforcement learning the three tasks using a limited number of objects. It provides a novel mechanism by which cognitive processes in the PFC can learn to influence visual processing by retrieving visual templates. Two limitations of this model should be outlined: first, it only considers the direct pathway of the BG, neglecting the indirect and hyperdirect ones; second, the mechanisms to encode the sample and the task cue in working memory in dlPFC are hard-coded and not learned. The first limitation was since overcome by an extension of this model including the indirect and hyperdirect pathways, with a strong emphasis on the dopamine-modulated plasticity in these pathways. This extended model was successfully used to explain cognitive deficits in various BG-related diseases, such as Parkinson’s disease (Schroll et al., 2014) and Huntington’s disease (Schroll et al., 2015). Flexible WM mechanisms to learn to maintain relevant information in dlPFC are presented in the next section (Schroll et al., 2012).
Insights on the role of DA
Dopamine regulates plasticity in the projections to the BG, but also between the different nuclei of the BG. Its phasic component carries a reward-prediction error that reinforces successful stimulus-response associations. DA-mediated plasticity occurs only in the acquisition phase, when the success of a response is not predicted yet. When a striatal representation is associated with reward delivery, it cancels dopaminergic activation and suppresses learning.
1.6.3 Chapter 4 : WM and multiple basal ganglia loops
Updating and maintaining information in WM is a complex cognitive process involving mainly the dlPFC and the BG (Frank et al., 2001), although many other cortical areas play a significant role (Ashby et al., 2005; Jonides et al., 1998). Many neuro-computational models consider that the BG is involved only in WM updating, i.e. the conditional entry of stimuli into it (Helie et al., 2013; Uttal, 2015). One of the most prominent models of WM (O’Reilly and Frank, 2006) for example considers the BG as a gating mechanism allowing, based on reinforcement learning, sensory information to enter recurrent loops within the PFC. It has among others been applied to the complex 1-2-AX task, which can be described as followed: a sequence of letters (A, B, X, Y) and digits (1, 2) is displayed on a screen. The subjects have to respond with the left button if they see an A followed by an X, but only if the last digit they saw was a 1. If that last digit was a 2, they have to press left when they see a B followed by a Y. In all other cases, they have to press right.
The 1-2-AX task is very complex, even for humans. It involves maintaining two levels of information in WM: what was the last digit I saw (outer loop) and have I just seen an A or a B (inner loop)? If these two pieces of information are kept in WM, deciding whether to press left or right when an X or Y appears becomes as trivial as a stimulus-response association. The difficulty is to know how a system can learn to maintain the outer and inner loops based solely on reinforcement learning, i.e. without explicit knowledge of the task. O’Reilly and Frank (2006) solve the problem by implementing three parallel PFC/BG loops, one learning to maintain 1 and 2, another A and B and the last one X or Y. The structural credit assignment problem - if the response is incorrect, which of these three loops has failed? - is solved by allowing each loop to modulate its own dopaminergic reward signal, but these loops are mostly independent of each other. Moreover the BG are only used to update WM content, not actually maintain it, contrary to experimental evidence (Landau et al., 2009).
In Schroll et al. (2012), we proposed a neuro-computational model of WM updating and maintenance involving three PFC-BG loops: two associative loops and a motor one. The role of the motor loop is to decide which motor response (left or right) should be executed based on short-term mnemonic information maintained in the associative loops during a 1-2-AX task. The role of the two associative loops is to learn to maintain the outer (1 and 2) and inner (A and B) loops, respectively. Based on an idea by Krueger and Dayan (2009), we posit that shaping plays an important role in organizing the different loops: animals usually don’t address complex cognitive tasks directly, but incrementally generate more and more complex behavior by reusing abilities that were previously acquired. In the case of the 1-2-AX task, this would correspond to responding first to a 1 or 2, then to 1 followed by A or 2 followed by B, and finally by the 1-2-AX task task itself. Once a subtask is mastered, errors in performance can be interpreted as a change in task complexity, signaling that more cognitive resources should be allocated to solve the problem.
In the first shaping phase (only digits are presented), the motor PFC/BG loop learns to respond appropriately using the same mechanisms as in Vitay and Hamker (2010). When the second phase is introduced (A-X or B-Y), the motor loop can not solve the problem because it has no memory of the last digit seen. One of the two associative loops then starts learning to maintain this information through a closed loop. The sustained activation of a digit then biases the motor loop to respond correctly to a 1-A or 2-B association. Finally, when the full 1-2-AX task is introduced, the associative and motor loops fail again, as only the outer loop is maintained. The associative loop sends a “distress” signal, telling the other associative loop to help solve the task. The new loop then learns to maintain A and B, providing enough information to the motor loop to execute the correct motor response.
Associative PFC/BG loops learn from errors as long as they are not confident in their output. When they become confident but the whole behavior fails, they ask for more cognitive resources to be allocated to the task instead of simply unlearning what they were previously correctly doing. Communication between the loops and the subsequent recruitment of cognitive resources is based on the spiraling striato-nigro-striatal connectivity (Haber et al., 2000): each loop has its own dopaminergic signal, which can be activated by loops higher in the hierarchy. When the first associative loop fails to solve the task although it was previously performing well, it signals the second loop through its dopaminergic system that it should get engaged in order to improve the organism’s ability to acquire rewards.
Monitoring of performance is a crucial mechanism by which cognitive resources can be allocated to solve a problem. The brain does not relearn everything every time it is confronted with a new problem, it first tries already acquired solutions and only tries to combine or update them when the performance is not satisfying (Botvinick et al., 2009). Based on neuro-anatomy and the functional importance of dopamine in goal-directed behavior, the spiraling structure of the striato-nigro-striatal system is a good candidate to coordinate the flexible recruitment of PFC-BG loops. However, the anterior cingulate cortex (ACC) is known to be crucial in self-performance assessment and error monitoring. As ACC is involved in a PFC-BG loop located just in between the limbic regions (OFC, vmPFC) and the associative ones (dlPFC) (Haber and Knutson, 2010), its dominating position may be the crucial link to determine the involvement of different associative loops to solve cognitive problems. In all cases, understanding how the dopaminergic system processes reward expectations and errors in these different loops is important for the understanding of the organization of PFC-BG loops.
Insights on the role of DA
The activation of dopaminergic neurons is not uniform but specific to each PFC-BG loop. Different loops can control their learning ability by modulating their influx of dopamine. Moreover, the hierarchical organization of the reciprocal connections between the striatum and the dopaminergic areas allows the flexible recruitment of cognitive resources when needed.
1.6.4 Chapter 5 : Timing and expectation of reward
The TD error signal depends only on two pieces of information: the prediction of the value of a state (or action) and the reward actually received. As shown on Figure 1.7, VTA receives information from many other brain regions: a massive inhibitory projection from NAcc (possibly excitatory through a relay on the ventral pallidum - VP), direct cortical excitation from the PFC, excitatory connections from reward-related brainstem regions such as the pedunculopontine tegmental nucleus (PPTN), the lateral habenula (LHb) or the lateral hypothalamus (LH). As discovered recently, it also receives inhibitory connections from the mesopontine rostromedial tegmental nucleus (Bourdy and Barrot, 2012; RMTg, Jhou et al., 2009). Inhibitory neurons in the VTA furthermore control the activity of VTA cells and project on NAcc and PFC. The complexity of the afferent system to VTA suggests that it computes more than a simple reward-prediction error signal.
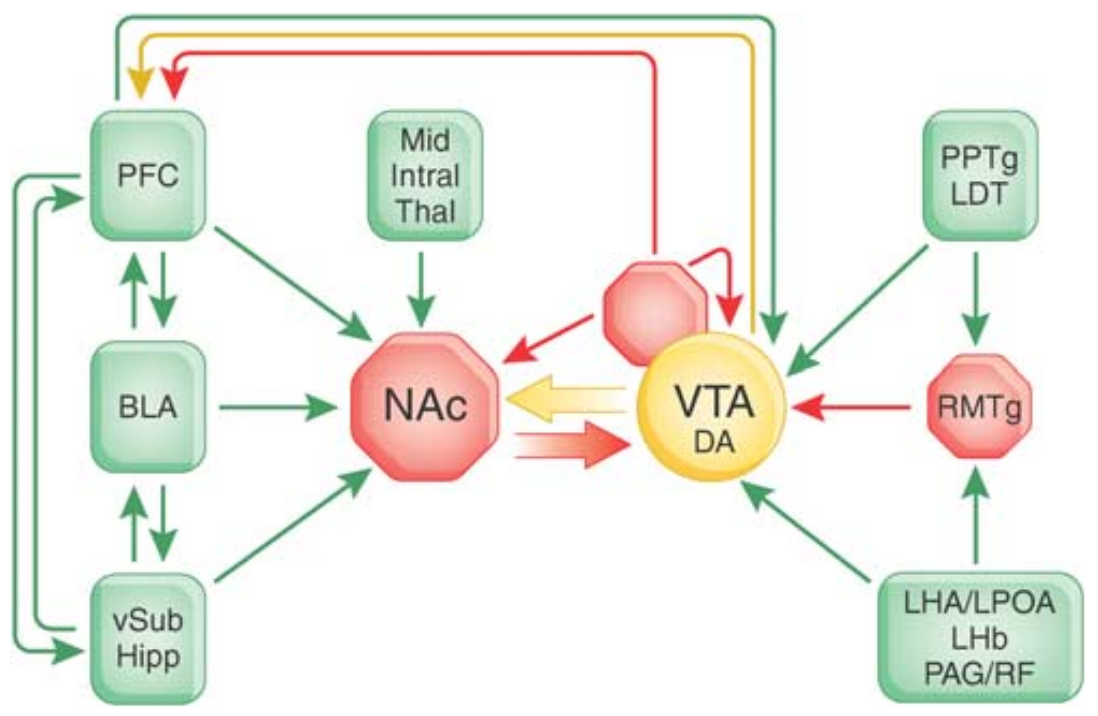
Several neuro-computational models of the dopaminergic system have been proposed to explain this organization (Brown et al., 1999; O’Reilly et al., 2007; Tan and Bullock, 2008). A common point of these dual-pathway models is that they distinguish the excitatory and inhibitory components driving VTA activity for rewards and reward-predicting stimuli, although some debate exists on the exact structures carrying these informations. The DA burst in response to delivery of reward likely originates from the PPTN, while the cancellation of this response when the reward is fully predicted originates from the striatum. Reward-predicting stimuli activate VTA either though the excitatory projection from PFC or from the amygdala. The main difference between those models is how the temporal component of the DA signal is computed: in the experiments of Schultz et al. (1997), VTA shows a dip below baseline at the exact time where a reward was expected but did not occur. As no sensory event happens at this time, this indicates that internal timing mechanisms are involved in generating the DA signal.
The hypothesis taken by Brown et al. (1999) and Tan and Bullock (2008) is that the striatum implements a spectral timing mechanism (Grossberg and Schmajuk, 1989) where striatal neurons have intracellular calcium levels which peak at different times after stimulus onset: detecting these peaks allows to estimate the time elapsed since onset. Because of the lack of evidence for such a mechanism, we decided in Vitay and Hamker (2014) to investigate alternative mechanisms for interval timing. A successful model of interval timing is the Striatal-Beat Frequency model (Matell and Meck, 2004). The basic principle is that cortical neurons behave as oscillators at different frequencies which are synchronized at stimulus onset. The population code composed by these oscillators provides a unique description of the time elapsed since onset: if enough neurons and a large enough range of frequencies are used, the population will never display twice the same pattern, while being reproducible between different trials. Striatal neurons can then detect the elapsed duration by learning to respond to the cortical pattern present when reward is delivered: the DA burst at reward delivery influences plasticity at corticostriatal synapses so they become selective only for that pattern. This model captures many aspects of the link between dopaminergic activity and timing processes, including the accelerated sense of time when DA is elevated - for example in aroused states or during recreational drug use - or the effect of lesions of SNc/VTA or the striatum on interval timing (Coull et al., 2011).
Using this hypothesis, we developed a novel neuro-computational model shedding new light on the afferent system to VTA based on neuro-anatomical evidence. Although the response to primary rewards is classically mediated through PPTN, we propose that conditioned stimuli activate VTA through the existing connection between the amygdala - a structure known for its involvement in classical conditioning - and PPTN. Furthermore, we propose that the cancellation of the DA burst when a reward is predicted and the DA dip when a reward is omitted are processed by two different mechanisms: the direct inhibitory projection from NAcc to VTA can inhibit the response to primary rewards, but bringing VTA activity below baseline requires a complex sub-network linking the ventral BG (NAcc and VP) to VTA through LHb and RMTg.
The model is able to reproduce a wealth of experimental findings: the progressive appearance of phasic bursts at CS onset through classical conditioning, the progressive canceling of the amplitude of the phasic bursts elicited by primary rewards, the strong phasic inhibition at the time when reward is expected but not delivered, the dependency on reward magnitude of the activities in BLA and VTA, the response to reward delivered earlier than expected (Fiorillo et al., 2003; Pan and Hyland, 2005; Schultz et al., 1997). This model is currently limited to VTA activity during classical conditioning but provides a detailed functional basis to address the mechanisms of dopamine release in the PFC-BG system.
Insights on the role of DA
The dopaminergic system integrates information from diverse structures, signaling reward delivery, prediction and omission through different projections. Cognitive, motor and emotional information converge on the dopaminergic system, which then redistributes back the most relevant aspects. It is critically involved in timing processes and therefore the organization of behavior through time.
1.6.5 Chapter 6 : Neural simulator ANNarchy
Neuro-computational models are described by a limited set of information:
- The number of populations of neurons (or areas), the number of neurons in each population and possibly a topology;
- A set of ordinary differential equations (ODE) describing the dynamics of each neuron model in the model;
- Connectivity patterns for the projections between the populations: all-to-all, probabilistic, distance-based, etc;
- A set of ODEs describing the dynamics of synaptic plasticity for the projections;
- Methods to provide inputs and read out outputs of the network.
Some of these informations can be inferred from anatomical and physiological data. Neural and synaptic dynamics are well studied, so only small modifications usually need to be applied to standard models. The main difficulty is actually to find sensible values for the free parameters of the model: time constants, learning rates, etc. Although experimental data constrain the range of possible values, this is the most time-consuming part of the design of a neuro-computational model.
Another difficulty is that neural networks can very quickly become expensive to simulate: the number of connections grow quadratically with the number of neurons and the computations can become very slow if no special care is taken about the optimality of the implementation. Parallel computing offers many advantages for the simulation of neural networks as each neuron only processes local information, but writing optimized parallel code on different hardware (shared-memory systems, distributed systems or recently general-purpose graphical cards - GPU) can be quite difficult and time-consuming.
Consequently, researchers in computational neuroscience use neural simulators instead of writing their own simulation code. These are libraries allowing the definition of a model, usually in a high-level scripting language such as Python or Matlab, and hiding from the user all the low-level implementation details necessary to run efficiently simulations in parallel. Another positive side effect is that neural simulators facilitate the exchange of models between researchers for validation and the integration of different models to obtain more functionalities.
Many different neural simulators are available to the community: NEURON, NEST, GENESIS, Brian, GeNN, Auryn Vitay et al. (2015). They all have different strengths and drawbacks: the exhaustiveness of the set of neural and synaptic models which can be included in a model, the simplicity of the interface, their optimization for a particular parallel hardware, etc. These simulators focus on the simulation of spiking networks, where neurons exchange information through discrete events (spikes), while rate-coded models, where neurons exchange directly a firing rate, are usually impossible or very difficult to define. At the exception of Brian, these simulators provide a fixed set of neural and synaptic models which can only be extended with great difficulty: as long as one only needs standard models, these simulators are very practical, but if one wants to investigate new mechanisms, the programming effort becomes important. Brian proposes a very flexible code generation approach, where neural and synaptic dynamics are described using a text-based equation-oriented mathematical description which is used to generate Python code at run-time (Stimberg et al., 2014). Using code generation allows the user to define virtually any neural or synaptic model.
In parallel to the design of the neuro-computational models presented above, I developed over several years a neural simulator named ANNarchy (Artificial Neural Networks architect), later in collaboration with Helge Ülo Dinkelbach. Two main principles guided the development: first, it should allow the rapid definition of neural networks, for both rate-coded and spiking models. Second, the simulation should be able to run transparently and efficiently on different parallel hardware (using OpenMP for shared-memory systems, MPI for distributed ones and CUDA for GPUs). Code generation is the core principle of the simulator: the definition of the network in a Python script is analyzed and used to generate entirely the simulation code (including a translation from the text-based description of ODEs to executable code statements), using templates adapted to the parallel framework.
In Vitay et al. (2015), we presented the neural simulator to the community and showed that its parallel performance is at least comparable to the alternatives. It is freely available and released under an open-source license. In addition to being used inside the professorship of Artificial Intelligence of the TU Chemnitz, several research groups have shown interest in this simulator and have started using it for their own research. More than just a tool, ANNarchy is also a very promising platform to study the issues raised by neuro-computational models to the parallel computing community: relying on code generation, it allows to explore systematically the different optimizations and algorithms that allow specific networks to be simulated efficiently on different hardware.
1.7 Conclusion
The common theme of this thesis is the role of dopamine in the cognitive, motor and emotional processes involved in goal-directed behavior. Using biologically-realistic neuro-computational models, I investigated its role in visual object categorization and memory retrieval (Vitay and Hamker, 2008), reinforcement learning and action selection (Vitay and Hamker, 2010), the updating, learning and maintenance of working memory (Schroll et al., 2012) and timing processes (Vitay and Hamker, 2014). The involvement of dopamine in such a wide variety of processes highlights the importance of understanding the mechanisms leading to dopamine release as well as its effect on the activity and plasticity of cortical and subcortical structures.
The different models outline different facets of the effect of DA release in the brain. In the cerebral cortex, the most important effect of DA is the modulation of synaptic transmission in localized networks of excitatory and inhibitory neurons. DA release in the prefrontal cortex influences short-term memory processes by inducing two modes of computation: an “open gate” mode, where multiple sensory information can enter the neural substrate and be represented in parallel; and a “closed gate” mode, where only the strongest and most important representation is maintained, allowing sustained activation (Seamans and Yang, 2004). The transition between these two modes follows an inverted U-curve, where low and high DA levels lead to open gates and intermediate levels to closed gates. The proposed model of PRh (Vitay and Hamker, 2008) exhibits a similar mechanism: PRh can switch between a representational state (driven by inputs) and a mnemonic state (where visual memory is retrieved) depending on the modulatory influence of DA on synaptic transmission. It is likely that DA is able to induce such different modes of computation in all cortical areas receiving dopaminergic input (the whole frontal lobe, the inferotemporal and parietal cortices). The functional consequences of this property still need to be explored, especially with respect to the spatial scale: do all these cortical areas receive the same dopaminergic input from VTA, or is there a functional topology allowing to selectively switch single areas?
In the basal ganglia, the main mode of action considered in the models is the inducement of plasticity by phasic DA bursts or dips. These short-term deviations around the baseline shape synapses coming from the cortex, but also inside the BG. Although more complex models of plasticity have been used, their influence basically follows a three-term DA-modulated Hebbian learning rule. DA bursts reinforce PFC/BG representations which lead to reward, while DA dips “punish” the ones which led to omission of reward or punishment (Schroll et al., 2012; Vitay and Hamker, 2010). This mechanism is fundamentally in line with actor/critic analogies. The short-term duration and the short latency of these phasic responses furthermore allow DA to signal precisely the occurrence of meaningful events, what can be used to learn time intervals and provide an internal sense of elapsed time (Vitay et al., 2015). One aspect of dopamine that will be addressed by future work is the influence of its tonic activity on the BG, which are known to influence the strength and vigor of motor responses as well as the exploration/exploitation trade-off (Beeler et al., 2010; Niv et al., 2007).
An important mechanism proposed in this work is how multiple PFC/BG loops can communicate by influencing each other’s dopaminergic signal. The striato-nigro-striatal connectivity is a remarkable anatomical property whose functional consequences remain largely unexplored. We proposed in Schroll et al. (2012) that it provides a mechanism allowing PFC/BG loops to recruit other loops when the task becomes too complex. The ability of each loop to control its dopaminergic input is here fundamental: by knowing how well it performs on a task, it can know if a mistake is its own responsibility, in which case it should continue learning, or if it should rather ask for more cognitive resources to solve the task. This mechanism is fundamental for life-long learning: complex behaviors emerge by composing already acquired simple behaviors, not by learning them from scratch. Future work will broaden this idea to other systems, especially the coordination between the limbic and associative loops which form the basis of goal-directed behavior.
Without a deep comprehension of the neural mechanisms underlying dopamine activity, it would be difficult to design artificial systems showing an intelligent and flexible organization of behavior. Research in computational neuroscience has therefore the opportunity to advance considerably artificial intelligence by transposing biological principles into flexible algorithms. In the proposed work, goal-directed learning focuses on extrinsic rewards. Intrinsic rewards are able to generate more interesting behaviors, such as the discovery of relevant information driven by curiosity or playfulness. Fortunately, dopamine influences similarly the structures responsible for these behaviors and the ones involved with extrinsic rewards, so the principles presented in this thesis will be useful to design such systems. However, intrinsic rewards require an internal state to be acted upon: a core idea of intrinsic motivation is that some actions are directed toward maintaining the system in its “comfort zone” - the homeostasis, for example maintaining the body’s temperature, satiety or safeness - while others on the contrary are the consequence of drives that can never be satiated - curiosity can for example never be completely satisfied, so it keeps the organism exploring its environment (see Oudeyer and Kaplan, 2007 for a typology of intrinsic motivation). This internal state obviously requires a body, so that actions acquire a better meaning than simply collecting external rewards. This outlines the importance of embodiment and future work will address the implementation of the proposed models on robotic platforms.
