4 Working memory and response selection: A computational account of interactions among cortico-basal ganglio-thalamic loops
Abstract
Cortico-basal ganglio-thalamic loops are involved in both cognitive processes and motor control. We present a biologically meaningful computational model of how these loops contribute to the organization of working memory and the development of response behavior. Via reinforcement learning in basal ganglia, the model develops flexible control of working memory within prefrontal loops and achieves selection of appropriate responses based on working memory content and visual stimulation within a motor loop. We show that both working memory control and response selection can evolve within parallel and interacting cortico-basal ganglio-thalamic loops by Hebbian and three-factor learning rules. Furthermore, the model gives a coherent explanation for how complex strategies of working memory control and response selection can derive from basic cognitive operations that can be learned via trial and error.
4.1 Introduction
Working memory (WM) is a key prerequisite for planning and executing responses. In a prominent notion (Repovs and Baddeley, 2006), WM consists of the capability to maintain information over limited periods of time and the ability to manipulate that information. By maintaining information in WM, an organism can detach its responses from its immediate sensory environment and exert deliberate control over its actions. Healthy human adults demonstrate an enormous flexibility in WM control in that WM is eligible for a tremendous multitude of stimuli, each of which can be maintained over adjustable periods of time and manipulated in various ways. However, that flexibility has to be acquired meticulously over many years of childhood and adolescence. In the early years of childhood, even WM tasks as simple as a Delayed-Match-to-Sample task pose a serious challenge (Luciana and Nelson, 1998).
While several brain structures have been shown to contribute to WM and response selection (cf. Bird and Burgess, 2008; Bunge et al., 2002; Jonides et al., 1998; McNab and Klingberg, 2008; Rowe et al., 2000), we here focus on the role of basal ganglia (BG) as part of a looped cortico-BG-thalamic architecture: closed cortico-BG-thalamic loops, connecting a particular area of cortex to itself, can be anatomically distinguished from open loops, linking in an ascending manner areas involved in motivation, cognition and motor execution (Haber, 2003; Voorn et al., 2004). This architecture of parallel and hierarchically interconnected loops provides a potential anatomic substrate for both WM processes and response selection: closed loops allow maintaining information for extended periods of time and flexibly updating it (i.e. two major WM processes); open loops allow information that is maintained in hierarchically superior WM loops to bias response selection within hierarchically inferior motor loops (cf. Haber, 2003).
With regard to plasticity, BG are assumed to take part in visual and motor category learning (Seger, 2008) and in establishing associations between stimuli and responses (Packard and Knowlton, 2002). Probably most eminently, they are believed to have an important role in reinforcement learning: BG receive dopaminergic afferents from substantia nigra pars compacta (SNc), a nucleus of the midbrain, that provides them with an error signal of reward prediction (Hollerman and Schultz, 1998; Schultz et al., 1997): Relative to a tonic baseline dopamine emission of nigral neurons, dopamine bursts result from unexpected rewards and from reward-predicting stimuli while dopamine depletions follow omissions of expected rewards. Dopamine levels have been shown to modulate long-term synaptic plasticity within BG, especially in its major input structure, the striatum (Reynolds et al., 2001; Shen et al., 2008).
In recent years, several computational models of BG functions have been developed, pinpointing their role in WM and motor control (Ashby et al., 2007; Brown et al., 2004; Gurney et al., 2001; O’Reilly and Frank, 2006; Vitay and Hamker, 2010). It has been shown that reinforcement learning mechanisms within biologically inspired cortico-BG-thalamic loops can solve conditional Delayed-Match-to-Sample and Delayed-Paired-Association tasks (Vitay and Hamker, 2010) and the 1-2-AX task of WM (O’Reilly and Frank, 2006). Moreover, it has been proven that shaping (i.e. a procedure of teaching a task via successively more complex approximations, Skinner, 1938) can provide computational models with benefits to learn demanding WM tasks (Krueger and Dayan, 2009): notably, shaping can speed up the learning process and provide sub-strategies to an agent that can later be used to cope with similar problems. In animal training and human education, shaping is a standard procedure to guarantee learning of complex behaviors: conditional WM tasks like the 1-2-AX task would not be trainable to animals or infant humans without such a procedure.
Given the huge variety of functions that BG contribute to and the multitude of brain areas that they interact with, a fundamental question in BG research is how different BG loops coherently interact. Here we follow a model-driven approach to gain insight into how dopamine-modulated learning in BG controls a combined WM-response selection system acting within different cortico-BG-thalamic loops. We propose a single set of Hebbian and three-factor learning rules for two different levels of the cortico-BG-thalamic hierarchy: prefrontal loops learn to flexibly switch between WM update and WM maintenance and a hierarchically inferior motor loop learns selection of rewarded responses based on WM content and visual stimulation. Our model’s functional abilities are demonstrated on delayed response (DR) tasks, a delayed alternation (DA) task and on the 1-2-AX task of WM (O’Reilly and Frank, 2006), the latter being trained in a three-step shaping procedure. We provide interpretations of the roles of BG pathways in WM control and response selection and propose a mechanism of how task monitoring for unexpected errors instigates learning processes. The purpose of our approach is to show how reinforcement learning processes within separate but interconnected cortico-BG-thalamic loops can in parallel establish WM control and response selection.
4.2 Material and methods
4.2.1 Architecture of the model
BG loops can be classified according to their contributions to different functional domains (Alexander et al., 1986): loops traversing the caudate nucleus and lateral prefrontal cortex contribute to the executive domain. They are involved in goal-directed learning, action-outcome associations and WM (Redgrave et al., 2010); loops traversing the putamen as well as premotor and sensorimotor cortices contribute to the motor domain and are involved in action selection, stimulus-response associations and habitual control (Horvitz, 2009). Different types of loops interact through various kinds of fibers (Haber, 2003). Among these fibers, cortico-striatal connections allow for a convergence of inputs from distinct frontal cortical areas onto key striatal regions (Calzavara et al., 2007; Takada et al., 1998). Thereby, these fibers create a hierarchy of information flow from the executive/prefrontal domain to the sensorimotor domain and provide a potential substrate for how cognitive processes guide motor processes (Calzavara et al., 2007). Figure 4.1 shows the general layout of our model which is consistent with cortico-BG-thalamic circuitry (Braak and Del Tredici, 2008; DeLong and Wichmann, 2007; Haber, 2003). The model consists of parallel and hierarchically interconnected cortico-BG-thalamic loops that all have the same general architecture and obey the same learning rules. Prefrontal cortico-BG-thalamic loops (as shown on the left of Figure 4.1) control WM by flexibly switching between maintenance and updating of information. They bias a motor loop (shown on the right of Fig. Figure 4.1) to decide between a set of possible responses. As previously motivated by others (e.g. Krueger and Dayan, 2009; O’Reilly and Frank, 2006), our model contains multiple independent prefrontal loops. While there is no upper limit to the number of loops that can be incorporated, we kept it as small as possible to minimize computational costs: two prefrontal loops are sufficient to have the model learn the tasks analyzed in this paper. Differential recruitment of these loops is controlled by the pedunculopontine nucleus (PPN) as detailed in the corresponding subsection below.
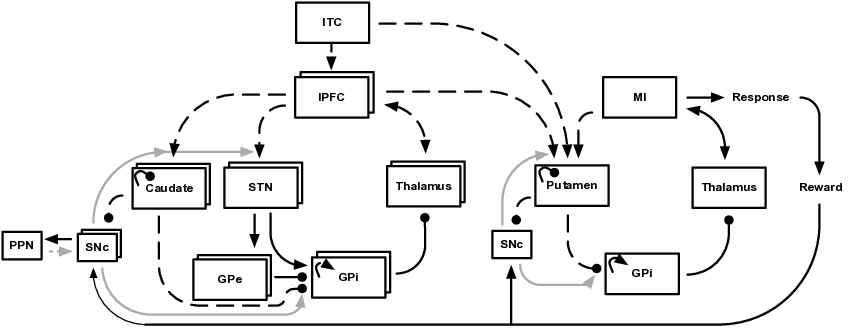
The general functional framework of our model is straightforward. During stimulus presentation, visual input is externally fed into inferior temporal cortex (ITC). Stimulus-related activity can then spread through the model and bias processing within prefrontal and motor loops. Motor responses are read out of primary motor cortex (MI) activity and rewarded if correct. When a reward is given, reward information is fed into SNc where an error signal of reward prediction is computed. From this error signal, BG learn to self-organize in such a way that the model’s responses maximize rewards.
The cortico-BG-thalamic loops’ functional architecture works as follows. Activation of cortex excites striatal and subthalamic neurons. Striatum then inhibits tonically active neurons of the internal segment of globus pallidus (GPi) via striato-pallidal connections that are usually referred to as the direct BG pathway. Decreases of GPi firing in turn disinhibit thalamic neurons that excitatorily connect back to cortex. In global terms, the direct pathway serves to establish WM maintenance within prefrontal loops by mapping cortical representations onto themselves. Within the motor loop, it links WM content to appropriate responses by mapping prefrontal-loop representations onto specific motor-loop representations. In contrast, activation of the subthalamic nucleus (STN) causes a strong and global excitation of GPi via subthalamo-pallidal fibers that are usually referred to as the hyperdirect pathway. As activity is spreading from STN to the external segment of globus pallidus (GPe), inhibitory GPe-GPi connections cancel the excitatory effects of STN on GPi. The hyperdirect pathway (which is modeled only in prefrontal loops) thus gives a brief and global reset pulse to GPi, allowing the respective loop to update. The interplay of the various layers will in detail be analyzed in Section 4.3.2.
In constructing the model, we included only those nuclei and pathways that were necessary to have the model perform response selection, WM maintenance and updating of WM. These functions are required by a set of prominent WM tasks (described in Section 4.2.2). As detailed later in this section as well as in Section 4.3.2, we assume response selection to be subserved by the direct pathway of the motor loop, WM maintenance by the direct pathway of prefrontal loops and WM updating by the hyperdirect pathway of prefrontal loops. We did not model the hyperdirect pathway of the motor loop and the ‘indirect’ striato-GPe-GPi pathway (within neither loop). As detailed in Section 4.4, empirical evidence implicates these pathways in functions other than the ones targeted in this paper. To keep the motor loop simple, pallido-pallidal, cortico-thalamic and thalamo-cortical connections were rendered hard-coded instead of learnable. Importantly: wherever a nucleus is present in both types of loops, activities are computed via the same equations. And: wherever a connection is learnable in both types of loops, the learning rules are the same.
The mathematical implementation of our model is inspired by a previous model from our group (Vitay and Hamker, 2010) that consists of a single-loop BG architecture without the ability to learn WM control: each of the modeled layers consists of dynamic, firing rate-coded neurons (exact numbers are reported in Table of the Appendix B). For each neuron, a membrane potential is determined via a differential equation, discretized according to the Euler method (first-order) with a time step of 1 ms; a cell-specific transfer function turns membrane potentials into firing rates. The differential equations are evaluated asynchronously to allow for stochastic interactions between functional units. As a general template, membrane potentials m^\text{post}_i(t) are computed by the following differential equation:
\tau \cdot \frac{d m^\text{post}_i(t)}{dt} + m^\text{post}_i(t) = \sum_{j \in \text{pre}} w_{i,j}^\text{pre-post}(t) \cdot u\text{pre}_j(t) + M + \epsilon_i(t) \tag{4.1}
where \tau is the time constant of postsynaptic cell $i,uprej(t) the firing rate of presynaptic cell $j,wpre-posti,j(t) the weight between these cells, MM a baseline parameter and \epsilon_i(t) a random noise term. The noise term supports exploration of WM control and action selection by introducing independent random fluctuations to the membrane potentials of different cells. Firing rates u^\text{post}_i(t) are computed from membrane potentials via cell-specific transfer functions f_u(x):
u^\text{post}_i(t)=f_u(m^\text{post}_i(t)) \tag{4.2}
As defined in Appendix A, f_u(x) defines negative values to be set to zero and for some layers additionally specifies sigmoid functions.
Loops are not predetermined to represent particular stimuli: each prefrontal loop receives the same visual input and only by accumulating knowledge about its environment will it learn to encode certain stimuli and ignore others. Figure 4.1 depicts all learnable connections of the model by dashed arrows. As explained in detail in the next paragraphs, thalamo-cortical and cortico-thalamic learning is Hebbian-like whereas learning in BG relies on three-factor rules, involving a reward-related dopaminergic term (Reynolds and Wickens, 2002). Dopamine levels are controlled by SNc firing rates and encode an error signal of reward prediction.
Dopaminergic learning poses an obvious challenge on modeling: as stimuli are typically presented (and responses performed) some time before reward delivery, there will be a delay between concurrent activity of pre- and postsynaptic cells and the dopamine levels resulting from that activity. The brain’s probable solution to this problem are synapse-specific calcium eligibility traces: concurrent pre- and postsynaptic activities lead to a sudden rise in input-specific postsynaptic calcium concentrations (Ca^\text{post}_{i,j}(t)) that decrease only slowly when concurrent activity ends.
\eta^\text{Ca} \cdot \frac{dCa^\text{post}_{i,j}(t)}{dt} + Ca^\text{post}_{i,j}(t) = f_\text{post}(u_i^\text{post}(t) - \overline{\text{post}}(t) - \gamma_\text{post}) \cdot f_\text{pre}(u_j^\text{pre}(t) - \overline{\text{pre}}(t) - \gamma_\text{pre}) \tag{4.3}
\eta^\text{Ca} = \begin{cases} \eta^\text{inc} \qquad \text{if } dCa^\text{post}_{i,j}(t) > 0 \\ \eta^\text{dec} \qquad \text{else.} \\ \end{cases} \tag{4.4}
\eta^\text{Ca} is the time constant of the calcium trace, \overline{\text{pre}}(t) the mean firing rate of afferent layer pre at time t, \overline{\text{post}}(t) the mean firing rate of postsynaptic layer post at time t, \eta^\text{inc} a parameter controlling the speed of calcium level increase and \eta^\text{dec} a parameter controlling the speed of calcium level decline. \gamma_\text{pre} and \gamma_\text{post} allow to adjust thresholds for pre- and post-synaptic activities that separate between increases and decreases of calcium traces. Functions f_\text{pre}(x) and f_\text{post}(x) can restrict pre- and post-synaptic terms to positive values or introduce sigmoid functions as detailed in Appendix A. dCa^\text{post}_{i,j}(t) gives a positive value when at the same point in time, both presynaptic cell j and postsynaptic cell i fire more than the adjusted mean activities of their respective layers. As \eta^\text{Ca} is set to the relatively small value of \eta^\text{inc} in that case, the corresponding calcium level increases rapidly. In contrast, dCa^\text{post}_{i,j}(t) becomes negative when concurrent activity ceases. As \eta^\text{Ca} is set to a relatively large value (\eta^\text{dec}) in that case, the calcium level does not directly drop to zero but declines rather smoothly. Calcium eligibility traces are inspired by findings that calcium levels stay heightened for some interval longer than actual pre- and postsynaptic activities (Kötter, 1994) and that postsynaptic calcium is required for striatal dopamine-mediated learning (Cepeda et al., 1998; Suzuki et al., 2001).
To determine changes in BG-related weights (w_{i,j}^\text{pre-post}(t)), a three-factor learning rule is used, comprising the calcium trace described above (which contains the two factors pre- and postsynaptic activity) and a dopaminergic term (\text{DA}(t)) linked to reward delivery:
\eta \cdot \frac{dw_{i,j}^\text{pre-post}(t)}{dt} = f_\text{DA}(\text{DA}(t)-\text{DA}_\text{base}) \cdot Ca^\text{post}_{i,j}(t) - \alpha_i(t) \cdot (u_i^\text{post}(t) - \overline{\text{post}}(t))^2 \cdot w_{i,j}^\text{pre-post}(t) \tag{4.5}
\tau \cdot \frac{d \alpha_i(t)}{dt} + \alpha_i(t) = K_\alpha \cdot (u_i^\text{post}(t) - u^\text{MAX})^+ \tag{4.6}
f_\text{DA}(x) = \begin{cases} x \qquad \text{if } x > 0 \\ \varphi \cdot x \qquad \text{else.} \\ \end{cases} \tag{4.7}
\text{DA}(t) is the dopamine level of the respective loop at time t, \text{DA}_\text{base} the baseline dopamine level of 0.5, \alpha_i(t) a regularization factor, u^\text{MAX} the maximal desired firing rate of cell i, \varphi a constant regulating the strength of long-term depression (LTD) relative to the strength of long-term potentiation (LTP) and K_\alpha a constant that determines the speed of increases of \alpha_i(t). In case of a dopamine burst (i.e. when dopamine levels rise above baseline), all weights are increased in proportion to the strengths of their calcium traces; dopamine depletions (i.e. dopamine levels below baseline) decrease recently active synapses accordingly. The subtractive term of the equation ensures that weights do not increase infinitely: when connections are strong enough to push firing of a postsynaptic cell above a threshold defined by u^\text{MAX}, \alpha_i increases and all weights to that postsynaptic cell are decreased. This ensures homeostatic synaptic plasticity, i.e. it provides negative feedback to level excessive neuronal excitation (cf. Pozo and Goda, 2010 for a biological review on the phenomenon). Technically, the homeostatic term is derived from Oja’s rule (Oja, 1982), but \alpha_i is made dependent upon postsynaptic activity to avoid arbitrary parameter values. Biologically, homeostatic synaptic plasticity has been shown to arise from alterations in the composition and abundance of postsynaptic AMPA receptors (Pozo and Goda, 2010). Increases of \alpha_i can be fast or slow depending on the value of K_\alpha.
By applying a single set of learning principles to all loops, we show their flexibility to subserve two highly different functions, namely to establish flexible control of WM and to link distinct cortical representations in a stimulus-response manner, thereby linking WM to motor control. While the general learning rules for prefrontal and motor loops are the same, the parameter values regulating LTD in the case of dopamine depletion differ. In particular, LTD in prefrontal loops is assumed to be slower than in the motor loop. Functionally, this ensures that after a sudden change in reward contingencies (resulting in dopamine depletions), re-learning in the motor loop is faster than re-learning in prefrontal loops: attempts to map priorly relevant stimuli onto different responses will thus be undertaken faster than gating previously irrelevant stimuli into WM.
The following paragraphs will focus on the different functional parts of the model and more thoroughly explain the supposed architecture.
Cortex
The model contains the cortical structures of lateral prefrontal cortex (lPFC) and MI. lPFC is assumed to take part in WM control (Owen et al., 1999); MI integrates cortical and subcortical inputs to send an emerging motor command to the motoneurons of the spinal cord. As a simplification, we assume each visual stimulus and motor command to be represented by a single computational unit within cortex. All cortical cells receive excitatory thalamic input; lPFC additionally receives cortico-cortical afferents from ITC which is involved in visual object recognition. In the mammal brain, prefrontal cortex is innervated by dopaminergic fibers. Prefrontal dopamine has been shown to modulate WM processes (Seamans and Yang, 2004; Vijayraghavan et al., 2007). However, these dopamine signals appear to last for several minutes (Feenstra et al., 2000; Feenstra and Botterblom, 1996; van der Meulen et al., 2007; Yoshioka et al., 1996) and are therefore not well suited to reinforce particular stimulus-response associations in a timely precise manner. Within the model, learning of thalamo-cortical weights is therefore assumed to be Hebbian-like (i.e. to not be modulated by dopamine). As our model is essentially an account of how learning in BG guides the organization of cortico-BG-thalamic loops, we do not model prefrontal dopamine signals.
Thalamus
Thalamus is assumed to relay information to cortical areas (Guillery and Sherman, 2002) and to control cortical activation and deactivation (Hirata and Castro-Alamancos, 2010). Consistent with this, maintenance of a representation in WM and selection of a response require thalamic disinhibition through GPi in the model. Thalamic cells receive inhibitory pallidal and excitatory cortical input (cf. Figure 4.1). As with prefrontal cortex, there is evidence for dopaminergic innervation of the thalamus (Melchitzky and Lewis, 2001; Sánchez-González et al., 2005). The nature of the dopamine signals provided, however, has not yet been clearly elucidated. Conservatively, we thus assume cortico-thalamic learning to be Hebbian-like (i.e. not to be modulated by dopamine).
Striatum
There are two input structures to the BG: striatum and STN. Both receive glutamatergic cortical afferents and both are organized topographically (Ebrahimi et al., 1992; Miyachi et al., 2006). Striatum can be subdivided into putamen, receiving mostly motor-cortical afferents, and caudate nucleus, innervated by lPFC (Alexander et al., 1986). Next to excitatory cortical afferents, striatal cells receive inhibitory input from a network of GABAergic interneurons (Suzuki et al., 2001). In the model, these are hard-coded for means of simplicity and serve to downsize the number of striatal cells that become associated to each cortical representation. Activity of caudate nucleus has been shown to be negatively correlated with progress in reward-related learning (Delgado et al., 2005). Lesioning dorsolateral parts of the striatum leads to disabilities in stimulus-response learning (Featherstone and McDonald, 2004). Within the model, striatum learns to efficiently represent single or converging cortical afferents in clusters of simultaneously activated cells as previously shown by Vitay and Hamker (2010). Striatum gives rise to the direct BG pathway, that connects striatal cell clusters to single GPi cells. Thereby, it is vital both for WM maintenance and stimulus-response mapping.
Subthalamic nucleus
STN is considered part of the hyperdirect BG pathway that links cortex with GPi via two excitatory connections (Nambu et al., 2002). Also, STN excitatorily innervates GPe (Parent and Hazrati, 1995). Recently, STN has become a key target for deep brain stimulation (DBS) in Parkinsonian patients in order to alleviate dyskinesia (Kleiner-Fisman et al., 2006) and to improve mental flexibility (Alegret et al., 2001; Witt et al., 2004). STN DBS has been reported to cause WM deficits in spatial delayed response tasks (Hershey et al., 2008) and nn-back tasks (Alberts et al., 2008), thereby further underlining its contribution to cognitive processing. Electrical stimulation of STN in monkeys yields a short-latency, short-duration excitation of GPi, followed by a strong inhibition, the latter being mediated by GPe (Kita et al., 2005). Based on these findings, we assume STN within prefrontal loops to give a global (learned) excitatory reset signal to GPi that is canceled by STN-GPe-GPi fibers shortly after.
Globus pallidus external segment
The role of GPe in BG functioning is still rather elusive. Historically, GPe has been considered a relay station on a striato-GPe-subthalamo-GPi pathway, often referred to as the indirect BG pathway (DeLong, 1990). More recently, such a simple notion has been challenged and GPe has been hypothesized to have a more prominent processing function in BG (Obeso et al., 2006). Our model contains a reduced set of GPe connections, accounting for afferents from STN and efferents to GPi only. Thereby, GPe is modeled only in its potential contribution to the hyperdirect (and not the indirect) pathway.
Globus pallidus internal segment
The internal segment of globus pallidus is a major BG output structure receiving and integrating subthalamic, external pallidal and striatal input (DeLong and Wichmann, 2007). GPi has a high baseline firing rate by which it tonically inhibits thalamic neurons (Chevalier and Deniau, 1990). Striatal and GPe inputs inhibit GPi cells below this baseline, thus disinhibiting thalamic neurons and opening a gate for mutually excitatory cortico-thalamic loops (DeLong and Wichmann, 2007). Subthalamic input in contrast excites GPi, thus further inhibiting thalamic neurons and preventing cortico-thalamic loops from firing (Nambu et al., 2002). The interplay of afferents to GPi which is critical for the model’s functioning, will be studied in detail in Section 4.3.2 of this paper.
Lateral competition in GPi ensures that each striatal cell cluster connects to a single pallidal cell only. While this is of course a simplification, it reasonably reflects the much smaller number of pallidal cells relative to striatal ones (Lange et al., 1976). As shown in Eq. (A.23) of the Appendix A, lateral weights evolve according to an Anti-Hebbian learning rule.
Substantia nigra pars compacta
Inspired by the findings of Schultz and co-workers (Hollerman and Schultz, 1998; Schultz et al., 1997) and in line with other computational accounts of reinforcement learning O’Reilly and Frank (2006), we assume SNc neurons to compute an error signal of reward prediction. This signal is then relayed to BG to modulate learning of afferent connections. A detailed account of the underlying rationale can be found in Vitay and Hamker (2010). Briefly, SNc neurons compute a difference signal between actual and expected rewards and add the resulting value to a medium baseline firing rate of 0.5. Thereby, unexpected rewards lead to activities above this baseline while omissions of expected rewards result in decreases in SNc firing. Information about actual rewards is set as an external input while stimulus-specific reward expectations are encoded in learnable striato-nigral afferents.
Each prefrontal and motor loop is connected to a separate SNc neuron. This is based upon reports showing SNc to have a topographical organization and reciprocal connections with striatum (Haber, 2003; Joel and Weiner, 2000). Inspired by evidence showing SNc neurons to broadly innervate striatal subregions (Matsuda et al., 2009), we assume a single dopamine neuron to innervate all BG cells of a corresponding loop.
Pedunculopontine nucleus
As outlined above, the model contains multiple prefrontal loops. Following an idea by Krueger and Dayan (2009), recruitment of these loops is dependent upon error detection after prior successful task performance. The framework of our model allows us to develop a biologically plausible mechanism of error detection: highly unexpected errors (i.e. errors after prior successful task performance) lead to relatively large dips in SNc firing. These dips can be used as a signal to recruit additional SNc neurons, thereby enabling learning within additional prefrontal loops.
A potential anatomic substrate for subserving such a recruitment is a part of the brainstem named pedunculopontine nucleus (PPN). PPN has been associated to the phenomena of attention, arousal, reward-based learning and locomotion (Winn, 2006); activation of cholinergic fibers from PPN to SNc has been shown to recruit quiescent dopamine neurons (Di Giovanni and Shi, 2009). As PPN is innervated by many BG structures (Mena-Segovia et al., 2004), it presumably also receives information about reward prediction. In our model, PPN constantly receives input from the SNc. Whenever the most recently recruited prefrontal-loop SNc neuron fires below a fixed threshold of 0.05 because of a highly unexpected error, PPN sends an activation signal back to the SNc to recruit an additional SNc neuron. Through this simple operation, PPN subserves a basic form of task monitoring, reacting whenever unexpected omissions of reward occur. In employing this mechanism, we do not artificially decrease learning rates within those prefrontal loops that previously recruited SNc neurons belong to. This contrasts with the model of Krueger and Dayan (2009).
Of course, the mechanism we propose may be largely simplified: other brain areas than the PPN have been linked to error detection as well, in particular the anterior cingulate (Holroyd and Coles, 2002). Further, PPN output is not restricted to SNc but also reaches other BG nuclei, most notably STN (Winn, 2006). Thus, PPN will neither be the only brain structure involved in error detection nor will recruitment of dopamine neurons be the only way it assists in modulating learning in cortico-BG-thalamic loops.
4.2.2 Experimental setups
We demonstrate the model’s learning capabilities on DR tasks as well as on the 1-2-AX conditional WM task.
Delayed response and delayed alternation tasks
We trained the model on an unconditional DR task, a conditional DR task and a DA task. In all three tasks, the model is exposed to a continuous array of trials. Within each trial, it has to choose between two responses and is rewarded if it picks the correct one. When a network has performed correctly for 100 trials in a row, we assume it to have learned the task successfully. A failure is admitted if a network does not reach this criterion within 10,000 trials.
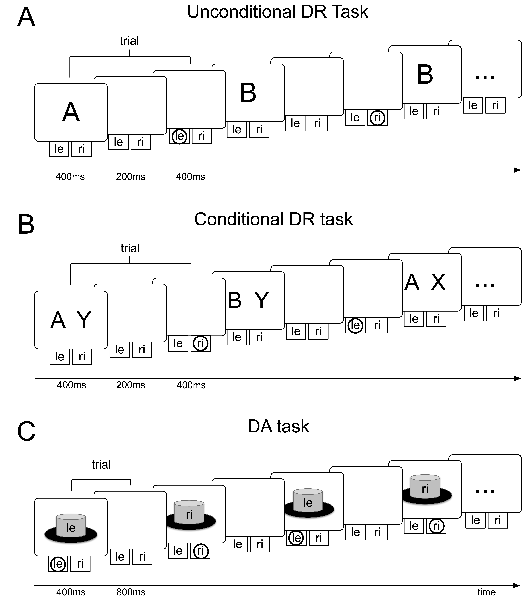
In the unconditional DR task (cf. Figure 4.2 (A)), one of two stimuli (i.e. either stimulus A or stimulus B) is presented for 400 ms at the beginning of each trial. After a delay period of 200 ms, the model’s response is evaluated. For stimulus A, the left button has to be selected while stimulus B requires a right-button press. The model has no prior knowledge about associations between stimuli and buttons. The conditional DR task (cf. Figure 4.2 (B)) differs from the unconditional DR task in that two stimuli are displayed and that both of them have to be considered to achieve a correct response: if stimuli A and X (or B and Y) have been shown, a left-button press is required while presentation of stimuli A and Y (or B and X) requires a right-button press. In the DA task (cf. Figure 4.2 (C)), the model is supposed to alternate between left- and right-button presses every 1200 ms. Reward is given whenever it chooses the button that it did not choose in the previous trial. For the DA task, we make the additional assumption that the model visually perceives the response that it decides for. Each response is thus fed into the model as a stimulus.
1-2-AX task
Within each trial of this task, one of a set of eight possible stimuli (1, 2, A, B, C, X, Y and Z) is shown and the model is required to decide for one of two buttons (cf. Figure 4.3). Only and exactly one of these buttons will lead to reward when pressed. The task has a complex inner-outer loop structure that is not known to the model: numbers (1 and 2) represent context cues and constitute the outer loop. To correctly perform the task, the last outer-loop stimulus has to be kept in WM at any time. Whenever the last outer-loop stimulus has been a 1, presentation of an X requires a right-button press when it has been directly preceded by an A; if the last outer-loop stimulus has been a 2, a Y that directly follows a B requires a right-button response. In all other cases, a left-button press has to be performed. The model has to decide for a response within each trial. There are several versions of this task regarding the sequence of stimuli. We will here use the version employed by O’Reilly and Frank (2006): First, an outer-loop stimulus (i.e. 1 or 2) is randomly chosen. Then, with equal probabilities, one to four inner loops are generated. With a probability of 0.5, an inner loop consists of a potential target sequence (i.e. A-X or B-Y); otherwise, any of the inner-loop stimuli (i.e. A,B or C) is followed by any of X,Y or Z, all probabilities being equal.
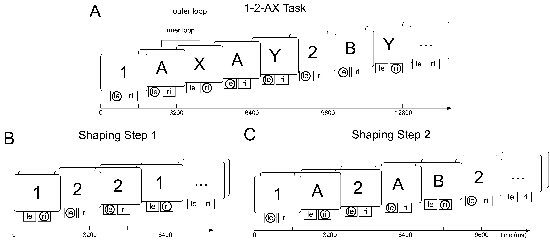
Teaching this task to the model requires a three-step shaping procedure as depicted in Figure 4.3. In a first step, only the outer-loop stimuli 1 and 2 are presented, probabilities being equal. Each 1 requires a right-button press, each 2 a left-button press. When the model has reliably acquired this task (which is conservatively assumed to be the case after 100 correct responses in a row), the inner-loop stimuli A,B and C are added to the sequence. An outer-loop stimulus can be followed by one or two inner-loop stimuli, all probabilities again being equal. A right-button press is required when an A comes up and the last number has been a 1 and when a B comes up and the last number has been a 2. In all other cases, a left-button press is required. Finally, when the second step is securely coped with, the full task is presented. After 150 correct responses in a row, the model is classified as having solved the task; if this criterion is not reached within 10,000 trials, we admit that the model has failed. In the first two steps of shaping, stimulus presentation (lasting for 400 ms) is separated from response requirement by a 400 ms delay period. This is to ensure that the model learns to make use of WM, preventing it from solving the task by simply associating visual ITC representations to responses. By employing the latter strategy, the model would not develop the ability to maintain the stimuli in WM as is required to successfully master the subsequent steps of shaping. For the full task, responses are required while visual stimulation is still on as proposed by O’Reilly and Frank (2006). Each stimulus is presented for 800 ms. 400 ms after each stimulus onset, the model’s response is evaluated.
4.3 Results
4.3.1 Task performance
Delayed response and delayed alternation tasks
Fig. Figure 4.4 (A) shows the model’s performance in learning the DR/DA tasks. For each of the three versions of the task, 50 randomly initialized networks were run. For each task, box plots show the number of trials needed until the last error occurs.
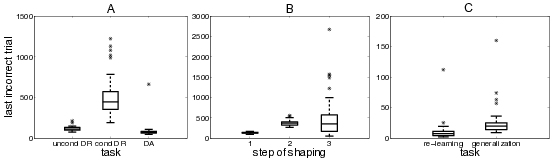
One network failed to learn to criterion. Two-sided Mood’s median tests provide difference statistics for the number of trials needed until the last error occurs. Thanks to the stability of these non-parametric tests in the presence of outliers, we kept the failing network for statistical analyses, charging the maximum number of 10,000 trials: the unconditional DR task (Mdn=111, IQR=33) requires significantly less trials than the conditional DR task (Mdn=443.5, IQR=221), \chi^2(1) = 92.16, p < 0.001. Clearly, this is because of its simpler rules. The DA task (Mdn=70.5, IQR=22) takes significantly less trials than both the unconditional DR task, \chi^2(1) = 51.84, p < 0.001, and the conditional DR task, \chi^2(1) = 84.64, p < 0.001.
1-2-AX task
Figure 4.4 (B) shows the performance of 50 randomly initialized networks learning the 1-2-AX task. For each step of the shaping procedure, box plots show the number of trials needed until the last error occurs.
All networks learned the task to criterion. Two-sided Wilcoxon signed-rank tests provide difference statistics for the number of trials needed to cope with the different steps: the second step of shaping (Mdn=365, IQR=78) takes significantly longer than the first step (Mdn=130, IQR=23), z=6.15, p<0.001, as can be explained by the more complex set of rules to learn and the higher number of additional WM representations to develop. The third step (Mdn=352.5, IQR=402) requires significantly more trials than the first step, z=5.49, p<0.001, but does not differ significantly from the second step, z=0.50, p=0.62. In the third step, a highly complex set of rules has to be learned while no additional WM representations have to be developed.
4.3.2 Analysis of the model’s behavior
Re-learning and generalization
To demonstrate the model’s abilities to profit from previous experiences, we evaluated its performance both in re-learning a task that has previously been learned and in generalizing from previous experiences to a new but structurally similar task. To this end, we trained 100 randomly initialized networks on the first two steps of the shaping procedure designed for the 1-2-AX task. Once the second step was learned to criterion, we again changed the rules: for 50 networks, we went back to the first step of shaping to evaluate re-learning. Note that learning the second step could have overwritten the knowledge acquired in the first step. For the 50 remaining networks, we changed the meanings of the two outer-loop stimuli to evaluate generalization. Previously, a right-button press had been required for an AA if the most recent number had been a 1 and for a BB if it had been a 2. Now it was required for an AA when the last number had been a 2 and for a BB when it had been a 1. Note that in this test for generalization the stimuli stay the same while responses have to be adapted.
Figure 4.4 (C) shows the model’s performance on these tests of re-learning and generalization. All networks learned to criterion. Difference statistics are based on two-sided Wilcoxon signed-rank tests. Re-learning the first step of shaping (Mdn=7.5, IQR=7) is significantly faster than the initial process of learning it (Mdn=129, IQR=25), z=6.15, p<0.001. Learning the generalization task (Mdn=19.5,IQR=11) takes significantly less trials than learning the first plus the second step of shaping (Mdn=493.5, IQR=112), z=6.15, p<0.001. Thus, the generalization task is learned a lot faster than the equally complex task that is learned during the first two steps of shaping. In fact, the generalization task is even learned significantly faster than both the first step of shaping by itself (Mdn=127.5, IQR=35), z=6.14, p<0.001, and than the second step of shaping by itself (Mdn=360.5, IQR=88), z=6.15, p<0.001. Thereby, it is clearly shown that the model profits from previous experiences: the more it has already learned about its environment, the better become its abilities to solve further problems.
Spread of activity within cortico-BG-thalamic loops
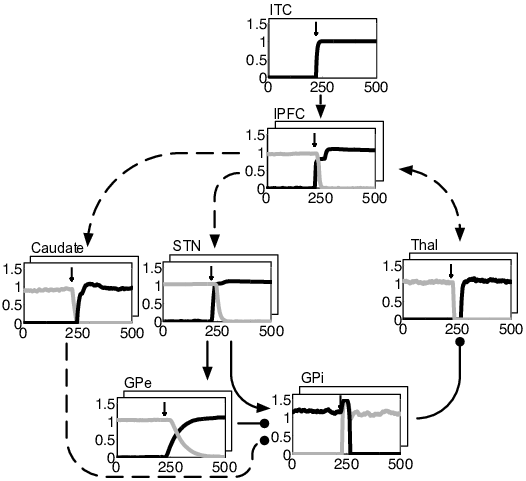
When a stimulus is presented to the model, it can either become maintained in WM or it fades away as visual stimulation ends. Figure 4.5 illustrates how a target stimulus-once associated to reward-is actively maintained in WM: when the target comes up in ITC, target-related activity (black line) is relayed to lPFC. lPFC then activates associated striatal and subthalamic cells. Subthalamic activity rises fast leading to a global increase in GPi firing via all-to-all excitatory connections. This breaks the circle of reverberating activity in the respective prefrontal loop, erasing any previously maintained stimulus (see gray lines) from WM. In the meantime, GPe activity rises through subthalamic excitation. By all-to-all inhibitory connections to GPi, GPe counterbalances the excitatory effect of STN on GPi and thereby-with a brief delay-brings WM reset to an end. As the previously maintained stimulus is erased from WM, target-related lPFC activity can activate striatal target-coding cells. Via inhibitory connections, these striatal cells then decrease firing of a GPi neuron that is associated to the target. This neuron in turn disinhibits a corresponding thalamic cell. Thalamus then excites cortex so that target-associated activity can reverberate in the prefrontal loop.
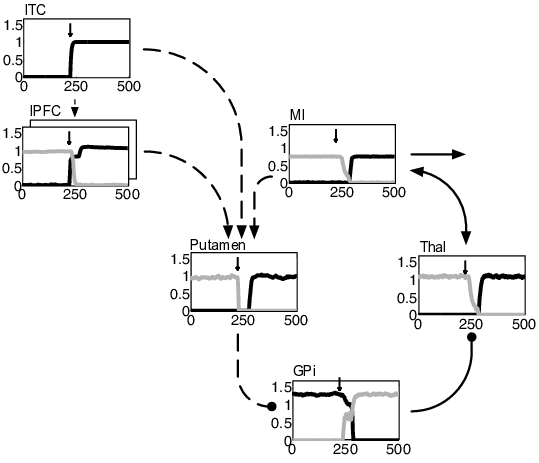
Figure 4.6 depicts the effects of target presentation on the motor loop: the target-coding cells within lPFC and ITC excite striatal cells of the motor loop. These cells then inhibit an associated GPi cell that in turn disinhibits a corresponding thalamic cell. Thalamus then excites the particular MI cell that codes the response that the target stimulus has been mapped on.
4.3.2.1 Development of WM control
Figure 4.7 shows the development of WM control. Firing rates are taken from a randomly initialized network learning the unconditional DR task. Infero-temporal, lateral prefrontal, striatal, subthalamic and pallidal activities of the prefrontal loop are shown for four periods along the process of learning (trials 1-5, 52-56, 91-95 and 129-133). The unconditional DR task we employed contains two stimuli, AA and BB. Black lines show firing rates of cells that can a posteriori be identified as having learned to code stimulus AA, gray lines correspond to stimulus BB.
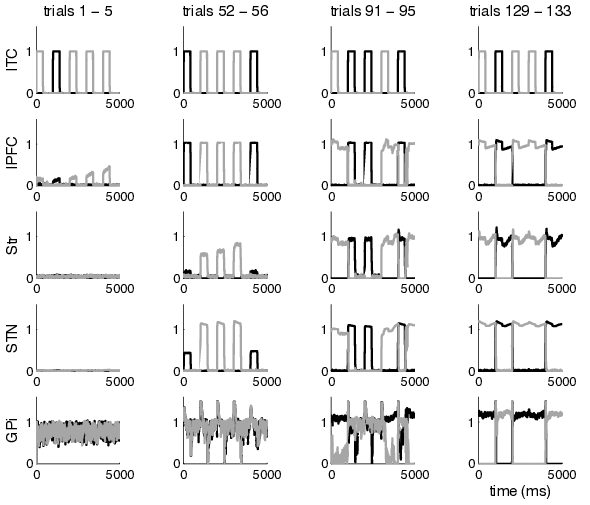
The leftmost column (trials 1-5) shows prefrontal-loop activities soon after the model is exposed to the task: lPFC task-related activities begin to emerge through the development of Hebbian connections from ITC. The corresponding lPFC cells have, however, not yet learned to activate striatal or subthalamic cells so that all representations fade away from WM when visual stimulation ends. Some decades of trials later (trials 52-56), cortico-subthalamic connections have largely developed as evidenced by the existence of task-related subthalamic activity upon stimulus presentation. Further, cortico-striatal connections have begun to emerge, resulting in some striatal activity upon stimulus presentation. Pallidal representations have not yet clearly developed as evidenced by the more or less uniform firing of GPi across trials. Thus, stimulus-associated activity cannot reverberate within cortico-BG-thalamic loops and lPFC representations still fade away when visual stimulation ends. Another four decades of trials later (trials 91-95), pallidal representations have started to evolve: stimulus BB (gray lines) shows clear task-related GPi activity (i.e. decreases of firing rates contingent upon stimulus presentation). This stimulus is now maintained in the loop independent of visual stimulation (which can be seen by ongoing activity after visual input ends). It can be concluded that a closed loop of connections that subserve the observed maintenance has been developed for this stimulus. Stimulus AA (black lines) however is still not clearly represented in the layers and mostly fades away when visual input ceases. The rightmost column shows the network when it has fully learned the DR task (trials 129-133): all brain areas show clear task-related activities. Both stimuli are maintained throughout the delay periods. Notice that when a stimulus is presented twice in a row, WM is not reset in between.
Recruitment of prefrontal loops
As outlined in Section 4.2.1, in cases of unexpected changes of reward contingencies, PPN triggers the activation of quiescent SNc neurons through dips in dopamine levels. This behavior can be well observed in networks learning the 1-2-AX task (Figure 4.8).
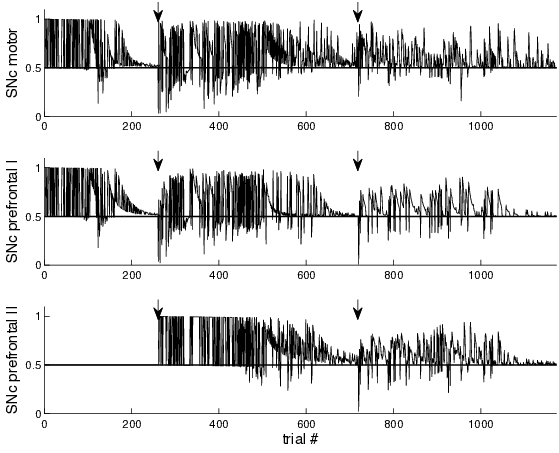
In the first step of shaping, two SNc neurons are active: the one neuron associated to the motor loop and one of the two neurons associated to prefrontal loops; the third SNc neuron is fixed to the baseline firing rate of 0.5 and awaits its activation by PPN. As the model learns the first step of shaping and becomes successful in predicting reward, firing rates of all active SNc neurons asymptotically approach baseline level (which can be seen around trial 200). As soon as the model has performed correctly for 100 trials in a row, the second step of shaping begins. Thereby, the rules of the task switch and the model cannot predict rewards accurately anymore. As it, however, still expects to be able to, SNc firing rates dip much below baseline. This activates the SNc neuron of the second prefrontal loop (as can be seen around trial 260). Around trial 700, the model has learned to cope with the second step of shaping and dopamine levels approach baseline again. After 100 correct responses in a row, the rules of the task switch again and SNc firing dips. This would now activate an SNc neuron of a third prefrontal loop (which, however, we did not include to save computational time as the tasks presented can be learned without it).
How shaping helps
To support the model in learning the 1-2-AX task, we train it using a three-step shaping protocol as described in Section 4.2.2. This protocol breaks down the inner-outer-loop structure of the task to assist the model in learning it. Figure 4.9 shows mean cortical activities for a network that successfully copes with the full 1-2-AX task. Firing rates of cells that belong to ITC and both parts of lPFC are each averaged over 100 consecutive trials.
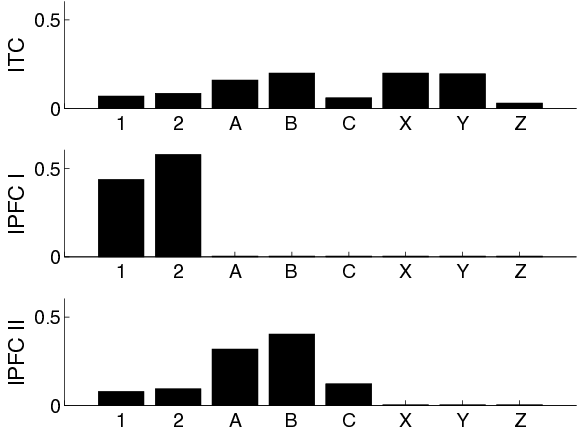
As described in Section 4.2.1, visual input is directly fed into ITC. Obviously therefore, ITC shows above-zero activities for all of the task’s stimuli. The different mean firing rates reflect the stimuli’s different probabilities of appearance as defined by the task. In particular, stimuli A,B,XA,B,X and YY are presented most often. lPFC activities are shown separately for the two prefrontal loops. Within the prefrontal loop which is subject to dopaminergic modulation directly, lPFC shows non-zero activities for stimuli 1 and 2. This indicates that this loop alternates between maintenance of the two outer-loop stimuli, ignoring all other stimuli. It thereby follows precisely the strategy of WM control that it has learned during the first step of shaping. The part of lPFC that belongs to the prefrontal loop which is recruited by PPN later shows strong activities for stimuli 1, 2, A,BA,B and CC. Clearly, these are the stimuli presented during the second step of shaping. This loop thereby maintains the last inner-loop stimulus that has been presented. From a global viewpoint, the model therefore maintains both the last outer-loop stimulus and the last inner-loop stimulus in WM at all times. In addition, ITC represents the stimulus presently shown. Via connections from ITC and lPFC to putamen, the motor loop is thus equipped with all the necessary information to choose its responses correctly: it receives information about the last outer-loop stimulus, the last inner-loop stimulus and the currently presented stimulus.
4.4 Discussion
We have shown how interactions among hierarchically interconnected cortico-BG-thalamic loops allow for flexible control of WM and for adaptive stimulus-response mappings. We thereby find that the anatomically well-defined cortico-BG-thalamic architecture is flexible enough to subserve both WM control and response selection. This implies that the same BG nuclei and pathways can subserve different functions on different levels of the system’s hierarchy. The striatum and its associated direct pathway allows for WM maintenance in prefrontal loops and for stimulus-response associations in motor loops. Within the cortico-BG-thalamic architecture, we show how complex strategies of WM control and response selection can be learned by methods of successive approximations and that these methods allow to generalize previously learned behaviors to new situations.
The need for shaping in complex WM tasks
As outlined above, the model relies on a three-step shaping procedure to solve the 1-2-AX task. To understand why shaping is vital to solve a complex task like that, it is necessary to understand its structure: in the 1-2-AX task, different stimuli have to be maintained in WM for differing periods of time. Moreover, they have to be updated independently depending on WM content and visual input. Specifically, outer-loop stimuli have to be deleted from WM only when the next outer-loop stimulus appears, while inner-loop stimuli have to be maintained for one trial only; all other stimuli should not be maintained at all. To make the task even more difficult, the model further has to learn how to correctly respond based on WM content. Decisions about rewards are based upon the final response only, not upon WM control. This poses the need of inferring both correct WM control and response behavior from a binary and thus relatively unspecific reward signal. One way to enable an agent to find out complex strategies of WM control and response behavior is to have it randomly permute the space of potential solutions (i.e. to try out each possible configuration of WM content and responses). O’Reilly and Frank (2006) employ such an approach. In their model, the maintenance of representations in WM is not subject to learning, only the gating of stimuli into WM. In order to learn correct WM control and stimulus-response associations, these stimuli must first be gated into WM, otherwise their information is lost before anything can be learned. To get the learning going, their model randomly gates stimuli into WM in an early phase of learning. Sooner or later, this will lead to finding the correct solution. However, such an approach is quite a computational effort and soon becomes practically infeasible as the number of potential stimuli and reactions increases. This is reflected in the much higher number of trials the PBWM model requires to learn the 1-2-AX task (being in the order of 30,000 compared to approximately 1000-1500 for our model, taking our definition of a trial). In contrast, our model allows each stimulus to enter lPFC and then learns WM maintenance and stimulus-response associations via calcium trace learning. As a consequence of this approach, our model does not learn the 1-2-AX task without a shaping procedure. While this might appear as a disadvantage at first sight, we consider it to be advantageous in terms of biological plausibility and flexibility: a human subject who is supposed to learn the 1-2-AX task without being told about its rules (and who has to find them find out through trial and error) will have a pretty hard time. Infant humans who cannot access a similarly broad range of previous experiences surely will not learn it without a shaping procedure. At the beginning of learning, our model does not have any knowledge, either (making infant learning a fair comparison). However, as outlined by Krueger and Dayan (2009), shaping allows an agent to develop sub-strategies for solving complex tasks. These can be kept in memory and be reactivated when an agent faces new but similar problems. Our model develops one sub-strategy within each step of shaping. When facing new tasks, it will use prior strategies in parallel with developing new ones and thus constantly enlarges its knowledge about its environment (cf. Section 4.3.2). By quickly re-learning previous WM-motor strategies and by generalizing from previous strategies (cf. Section 4.3.2), our model’s dependency on shaping for solving complex tasks gradually decreases. It thereby gives an explanation of how high-level cognitions can develop from basic cognitive operations.
Limitations of the model
The model employs a considerable number of simplifications: it does not contain the indirect BG pathway. This pathway and its predominantly D2-type dopamine receptors appear to be prominently engaged in learning to reverse dominant behaviors (Izquierdo et al., 2006; Lee et al., 2007; Tanimura et al., 2011). Also, the hyperdirect pathway of the motor loop has been omitted. Empirically, it appears to provide (relatively global) stop signals to prevent execution of responses (Aron and Poldrack, 2006; Eagle et al., 2008). This paper is restricted to the functions of response selection, WM maintenance and WM updating as required by most basic WM tasks. Therefore, we do not model these additional pathways. As a further simplification, we do not consider exact timing of responses: as stated in Section 4.2.2, the motor responses of the model are read out at predefined time-steps. Each decision about reward delivery thus depends upon the dominant response at only one particular time-step—and therefore neither upon the latency nor the duration of the response. Moreover, as the focus of this paper is on the contribution of BG reinforcement learning processes to the establishment of WM control and response selection, we do not provide an interpretation on the contribution of prefrontal dopamine signals to WM processes.
Comparison to other computational models of reinforcement learning in BG
A prominent account of the role of BG in WM is the PBWM model proposed by O’Reilly and Frank (2006). They provide a model of prefrontal cortico-BG-thalamic loop functioning, not including any explicit motor loop. This model requires BG for gating stimuli into prefrontal cortex while maintenance of information is subserved by locally self-excitatory prefrontal cortical loops; the direct and indirect BG pathways provide Go and NoGo signals for WM update, respectively. These assumptions contrast with our suppositions, implicating the whole cortico-BG-thalamic loop, via the direct BG pathway, in learning to maintain information (however, we agree that in well-learned tasks cortico-cortical connections might progressively take over control and supercede BG participation). Existing empirical evidence does not clearly favor one or the other assumption as several types of task-related activity seem to exist in striatal neurons. Cromwell and Schultz (2003) for instance found five such types in a spatial DR task. Consistent with our approach, one of these types showed sustained activity for the whole delay period. The relatively small number of cells in GPi (Lange et al., 1976) might at first sight argue against our hypothesis that WM maintenance is learned via cortico-BG-thalamic loops. But note that other types of connections (e.g. cortico-cortical ones) might develop as WM maintenance of a particular stimulus has been reliably learned, and release GPi to learn something new.
Ashby et al. (2007) propose a single-loop model of perceptual category learning (SPEED) that does not account for WM. They use a three-factor learning rule, much like ours, to map cortical representations onto striatal cells. However, BG learning is restricted to cortico-striatal connections, thus rendering their model less powerful in stimulus-response mapping. In particular, it will have severe problems mapping stimuli onto responses when relevant information lies within stimulus compounds instead of single stimuli. By allowing cortico-cortical connections to shortcut BG in case of well-learned, automatic behavior, however, their model provides an interesting concept beyond the scope of our model.
Brown et al. (2004) present an account of how learning within a single cortico-BG-thalamic loop assists in deciding between reactive and planned behaviors. Their TELOS model manages to learn several saccadic tasks and offers much anatomical detail. The authors assume cortico-cortical learning to be subject to the same phasic dopamine modulation as learning between cortex and BG. As explained above, this assumption is somewhat challenged by the long-lasting nature of prefrontal dopamine signals. WM is modeled as a hard-coded entity that is anatomically restricted to PFC: visual representations are predetermined to be gated in when PFC activity surmounts a certain threshold and to be deleted from it when the next sufficiently strong input appears.
Vitay and Hamker (2010) propose a computational account on how learning in BG guides visual attention in Delayed-Match-to-Sample and Delayed-Paired-Association tasks. The model contains only one cortico-BG-thalamic loop which is connected to infero-temporal cortex. It does not have the abilities to learn WM control. BG connectivity is restricted to the direct pathway. We here adapt and extend their account to model WM and motor control. To that end, we kept the general procedure of computing membrane potentials and firing rates. We also kept the concept of three-factor learning rules within BG—but sophisticated them to contain calcium eligibility traces. We newly devised an architecture of parallel cortico-BG-thalamic loops and allowed for interactions among these loops. We included additional BG nuclei and pathways and made the lateral inhibition in GPi independent of dopaminergic modulation to improve the model’s performance and to be in better accord with empirical data.
Predictions
Our model provides falsifiable predictions with regard to both behavioral and electrophysiological data. It predicts that re-organization of overt responses (i.e. within motor loops) is faster than a re-organization of WM control (i.e. within prefrontal loops). In particular, tasks that can be learned by utilizing a previously valid strategy of WM control (i.e. tasks in which only responses have to be adapted) will be learned significantly faster than tasks for which no previous strategy of WM control is available (cf. Section 4.3.2). Experimentally, this can be investigated by training animals or infant humans on the unconditional DR task described in Section 4.2.2 and by then changing the rules without announcement. In one condition, the same stimuli as in the original DR task will be used, but responses will have to be reversed to obtain reward. In the other condition, two new stimuli will be introduced, each of which has to be associated to one of the two responses. Our model predicts that the first condition will be learned significantly faster than the second one. The experimenter should use stimuli that the animal or infant has never seen before.
As we designed our shaping procedure to optimally suit the learning algorithms of our model, experimental evidence about the procedure’s adequacy tells about the biological plausibility of our algorithms. For the 1-2-AX task, we propose that in a first step of shaping, only the outer-loop stimuli 1 and 2 should be presented while in a second step, the outer-loop stimuli plus the inner-loop stimuli A,BA,B and CC should be shown. The efficiency of this procedure can for instance be compared to the protocol that Krueger and Dayan (2009) propose to train an LSTM network (Hochreiter and Schmidhuber, 1997). Showing our procedure to establish the desired behavior faster and more reliably will be a piece of evidence for the biological plausibility of our approach.
Neurophysiologically, our model makes clear predictions about the functions of BG nuclei: STN (via the hyperdirect pathway) is assumed to provide reset signals for WM update in prefrontal loops. STN lesions that are confined to prefrontal loops should thus result in severe difficulties to flexibly update WM. We predict that those lesions will cause failures to delete previously maintained stimuli from WM in delayed match to sample tasks. This will show up as perseverative errors, i.e. subjects will continue to base their answers on stimuli that were relevant in previous trials. The caudate nucleus (via the direct pathway) is supposed to support WM maintenance. Lesions should result in impairments to learn maintenance of stimuli in WM. In a delayed match to sample task, this will show up as an increase in ‘random’ (i.e. unsystematic) errors. Putamen is supposed to establish associations between WM content and appropriate responses. Lesions will cause severe impairments in learning stimulus-response associations. The impact on well-learned behavior, however, is less clear due to a potential buildup of cortico-cortical connectivity. Another physiological prediction is the increase in the number of active SNc neurons when a highly expected reward does not occur (i.e. after reward contingencies change in an unpredictable way). PPN lesions should attenuate SNc recruitment. Heightened SNc activity is supposed to correspond with an increase in alertness and concentration.
Conclusion
We propose an anatomically detailed computational model of how reinforcement learning contributes to the organization of WM and overt response behavior. To our knowledge, our model is the first to prove the functional flexibility of cortico-BG-thalamic loops: we show that both WM control and response selection can develop in parallel within separate but interacting loops. Within this framework, we show how complex cognitive operations can develop from basic strategies of WM control and response selection.
Acknowledgments
This work has been supported by the German Research Foundation (Deutsche Forschungsgemeinschaft) grant “The cognitive control of visual perception and action selection” (DFG HA2630/4-2) and by the EC Project FP7-ICT “Eyeshots: Heterogeneous 3-D Perception across Visual Fragments”.
Appendix A. Full list of equations
We here give a full overview on the model’s equations that will allow to reproduce the model. To facilitate reading and allow for an easy comparison, all parameters are shown in Table and Table . Equation 4.4, Equation 4.6 and Equation 4.7 of the main text identically apply to all learning rules unless a deviation is specified.
Cortex
Membrane potentials (m_i^\text{Cx}(t)) and firing rates (u_i^\text{Cx}(t)) of prefrontal and motor cortical cells are given by
\tau \cdot \frac{d m_i^\text{Cx}(t)}{dt} + m_i^\text{Cx}(t) = w_{i,i}^\text{Cx–Cx} \cdot u_i^\text{ITC}(t) + \sum_{j \in \text{Thal}} w_{i,j}^\text{Thal–Cx}(t) \cdot u_j^\text{Thal}(t) + M + \epsilon_i(t)
u_i^\text{Cx}(t) = \begin{cases} 0 \qquad \text{if } m_i^\text{Cx}(t) < 0 \\ m_i^\text{Cx}(t) \qquad \text{if } 0 \leq m_i^\text{Cx}(t) \leq 0.7 \\ 0.2 + \frac{1}{1 + \exp \frac{0.7 - m_i^\text{Cx}(t)}{2} } \qquad \text{if } m_i^\text{Cx}(t) > 0.7 \end{cases} \tag{4.8}
ITC simply reproduces sensory input. As motivated by Vitay and Hamker (2010), the transfer function of Equation 4.8 ensures that a broad range of membrane potentials above the value of 0.75 results in a relatively constant firing rate. This guarantees more stability in maintaining eligible WM representations in prefrontal loops when visual stimulation ends. Thalamo-cortical weights (w_{i,j}^\text{Thal-Cx}(t)) are updated according to
\eta \cdot \frac{d w_{i,j}^\text{Thal-Cx}(t)}{dt} = (u_j^\text{Thal}(t) - \overline{\text{Thal}}(t)) \cdot (u_i^\text{Cx}(t) - \overline{\text{Cx}}(t) - \gamma)- \alpha_i(t) \cdot (u_i^\text{Cx}(t) - \overline{\text{Cx}}(t))^2 \cdot w_{i,j}^\text{Thal-Cx}(t)
The threshold parameter \gamma ensures that only those prefrontal cells become associated to thalamic neurons that are activated by visual stimulation (i.e. not just by random noise). Weights are impeded to decrease below zero. Cortico-cortical weights from ITC to lPFC (w_{i,j}^\text{Cx-Cx}(t)) are updated according to:
\begin{aligned} \eta \cdot \frac{d w_{i,j}^\text{Cx-Cx}(t)}{dt} & = (u_j^{\text{Cx}_\text{ITC}}(t) - \overline{\text{Cx}_\text{ITC}}(t))^+ \cdot (u_i^{\text{Cx}_\text{PFC}}(t) - \overline{\text{Cx}_\text{PFC}}(t)) \\ & - \alpha_i(t) \cdot (u_j^{\text{Cx}_\text{ITC}}(t) - \overline{\text{Cx}_\text{ITC}}(t)) \cdot ((u_i^{\text{Cx}_\text{PFC}}(t) - \overline{\text{Cx}_\text{PFC}}(t)) \cdot w_{i,j}^\text{Cx-Cx}(t) \\ \end{aligned}
Weights are not allowed to decrease below zero.
Thalamus
Membrane potentials (m_i^\text{Thal}(t)) and firing rates (u_i^\text{Thal}(t)) of thalamic neurons are governed by
\tau \cdot \frac{d m_i^\text{Thal}(t)}{dt} + m_i^\text{Thal}(t) = w_{i,i}^\text{GPi–Thal} \cdot u_i^\text{GPi}(t) + \sum_{j \in \text{Cx}} w_{i,j}^\text{Cx-Thal}(t) \cdot u_j^\text{Cx}(t) + M + \epsilon_i(t)
u_i^\text{Thal}(t)=(m_i^\text{Thal}(t))^+
Cortico-thalamic weights (w_{i,j}^\text{Cx–Thal}(t)) are updated according to \eta \cdot \frac{d w_{i,j}^\text{Cx–Thal}(t)}{dt} = (u_j^\text{Cx}(t) - \overline{\text{Cx}}(t) )^+ \cdot (u_i^\text{Thal}(t) - \overline{\text{Thal}}(t) - \gamma) - \alpha_i(t) \cdot (u_i^\text{Thal}(t) - \overline{\text{Thal}}(t))^2 \cdot w_{i,j}^\text{Cx–Thal}(t)
Weights are impeded to decrease below zero.
Striatum
Membrane potentials (m_i^\text{Str}(t)) and firing rates (u_i^\text{Str}(t))) of striatal cells are governed by
\tau \cdot \frac{d u_i^\text{Str}(t)}{dt} + u_i^\text{Str}(t) = \sum_{j \in \text{Cx}} w_{i,j}^\text{Cx–Str}(t) \cdot u_j^\text{Cx}(t) + \sum_{j \in \text{Str}, j \neq i} w_{i,j}^\text{Str–Str} \cdot u_j^\text{Str}(t) + M + \epsilon_i(t)
u_i^\text{Str}(t) = (m_i^\text{Str}(t))^+
Cortico-striatal weights (w_{i,j}^\text{Cx-Str}(t)) are updated by the following calcium trace dependent three-factor learning rule:
\eta^\text{Ca} \cdot \frac{d \text{Ca}_{i,j}^\text{Str}(t)}{dt} + \text{Ca}_{i,j}^\text{Str}(t) = (u_j^\text{Cx}(t) - \overline{\text{Cx}}(t) - \gamma)(u_i^\text{Str}(t) \overline{\text{Str}}(t))^+
\eta \cdot \frac{ d w_{i,j}^\text{Cx-Str}(t)}{dt} = f_\text{DA} (\text{DA}(t) - \text{DA}_\text{base} ) \cdot \text{Ca}_{i,j}^\text{Str}(t) - \alpha_i(t) \cdot (u_i^\text{Str}(t) - \overline{\text{Str}}(t))^2 \cdot w_{i,j}^\text{Cx-Str}(t)
\gamma encourages weights to become negative, thereby instigating different inputs to connect to non-overlapping clusters of striatal representations.
Subthalamic nucleus
Membrane potentials (m_i^\text{STN}(t)) and firing rates (u_i^\text{STN}(t))) of STN cells are governed by
\tau \cdot \frac{d u_i^\text{STN}(t)}{dt} + u_i^\text{STN}(t) = w_{i,i}^\text{Cx-STN}(t) \cdot u_i^\text{Cx}(t) + M + \epsilon_i(t)
u_i^\text{STN}(t) = \begin{cases} 0 \qquad \text{if } m_i^\text{STN} (t) < 0 \\ m_i^\text{STN} (t) \qquad \text{if } 0 \leq m_i^\text{STN} (t) \leq 1 \\ 0.5 + \frac{1}{1 + \exp \frac{1 - m_i^\text{STN}(t)}{2} } \qquad \text{if } m_i^\text{STN}(t) > 1 \end{cases}
Cortico-subthalamic weights (w_{i,j}^\text{Cx-STN}(t)) are updated according to
\eta^\text{Ca} \cdot \frac{d \text{Ca}_{i,i}^\text{STN}(t)}{dt} + \text{Ca}_{i,i}^\text{STN}(t) = (u_i^\text{Cx}(t) - \overline{\text{Cx}}(t))^+ \cdot (u_i^\text{STN}(t) - \overline{\text{STN}}(t) -\gamma)^+
\eta \cdot \frac{d w_{i,i}^\text{Cx-STN}(t)}{dt} = f_\text{DA}(\text{DA}(t)-\text{DA}_\text{base}) \cdot \text{Ca}_{i,i}^\text{STN}(t)- \alpha_i(t) (u_i^\text{STN}(t) - \overline{\text{STN}}(t))^2 \cdot w_{i,i}^\text{Cx-STN}(t)
\gamma again ensures that only those prefrontal cells become associated to subthalamic neurons that receive visual stimulation. Weights are restricted to not decrease below zero.
Globus pallidus external segment
Membrane potentials (m_i^\text{GPe}(t)) and firing rates (u_i^\text{GPe}(t)) of GPe cells are given by
\tau \cdot \frac{d u_i^\text{GPe}(t)}{dt} + u_i^\text{GPe}(t) = w_{i,i}^\text{STN-GPe} \cdot u_i^\text{STN}(t) + M + \epsilon_i(t) u_i^\text{GPe}(t) = (m_i^\text{GPe}(t))^+
Globus pallidus internal segment
GPi membrane potentials (m_i^\text{GPi}(t)) and firing rates (u_i^\text{GPi}(t)) are ruled by
\begin{aligned} \tau \cdot \frac{d m_i^\text{GPi}(t)}{dt} + m_i^\text{GPi}(t) &= \sum_{j \in \text{Str}} w_{i,j}^\text{Str-GPi}(t) \cdot u_j^\text{Str}(t) + \sum_{j \in \text{GPi}, j \neq i } w_{i,j}^\text{GPi-GPi} \cdot (M - u_j^\text{GPi}(t))^+ \\ &+ \sum_{j \in \text{STN}} w_{i,j}^\text{STN-GPi} \cdot u_j^{STN}(t)+ \sum_{j \in \text{GPe}} w_{i,j}^\text{GPe-GPi} \cdot u_j^{GPe}(t) + M + \epsilon_i(t) \\ \end{aligned}
GPi has a high baseline firing rate; low GPi firing rates denote high activity in a functional sense. Lateral afferents therefore have the presynaptic term (M - u_j^\text{GPi}(t))^+: the lower the firing rate of a GPi cell, the higher its impact on other cells. The transfer function of Equation 4.9 ensures a slow increase of firing rates when membrane potentials rise above the value of 1.0. Striatal afferents are learnable while subthalamic and external pallidal inputs are assumed to be hard-coded for simplicity. Striato-pallidal inhibitory weights (w_{i,j}^\text{Str-GPi}(t)) evolve according to
\eta^\text{Ca} \cdot \frac{d \text{Ca}_{i,j}^\text{GPi}(t)}{dt} + \text{Ca}_{i,j}^\text{GPi}(t) = (u_j^\text{Str}(t) - \overline{\text{Str}}(t))^+ \cdot g(\overline{\text{GPi}}(t) - u_i^\text{GPi}(t))
g(x)= \frac{1}{1+\exp-2x} - 0.6 \tag{4.9} \eta \cdot \frac{d w_{i,j}^\text{Str-GPi}(t)}{dt} = - f_\text{DA}(\text{DA}(t)-\text{DA}_\text{base}) \cdot \text{Ca}_{i,j}^\text{GPi}(t) - \beta \cdot \alpha_i(t) \cdot (\overline{\text{GPi}}(t) - u_i^\text{GPi}(t))^2 \cdot w_{i,j}^\text{Str-GPi}(t) \tau_\alpha \cdot \frac{d \alpha_i(t)}{dt} + \alpha_i(t) = (-m_i^\text{GPi}(t) - 1.0)^+
The constant \beta attenuates the strength of the regularization term. The sigmoidal function g(x) guarantees selectivity of striato-pallidal mappings by ensuring a clear separation between GPi firing rates that favor an increase of striato-pallidal weights and those that favor a decrease of weights. \alpha_i(t) increases when (-m_i^\text{GPi}(t)-1.0) becomes positive. Weights are restricted to not become larger than zero. Lateral weights (w_{i,j}^\text{GPi-GPi}(t)) evolve according to
\eta \cdot \frac{d w_{i,j}^\text{GPi-GPi}(t)}{dt} = (\overline{\text{GPi}}(t) - u_j^\text{GPi}(t))^+ \cdot (\overline{\text{GPi}}(t) - u_i^\text{GPi}(t))^+ - \beta \cdot \alpha_i(t) \cdot (\overline{\text{GPi}}(t) - u_i^\text{GPi}(t))^2 \cdot w_{i,j}^\text{GPi-GPi}(t)
Weights are restricted to not become smaller than zero.
Substantia nigra pars compacta
Membrane potentials (m_i^\text{DA}(t)) and firing rates (u_i^\text{DA}(t)) of SNc cells are given by
\tau \cdot \frac{d m_i^\text{DA}(t)}{dt} + m_i^\text{DA}(t) = R(t) + P(t) \cdot \sum_{j \in \text{Str}} w_{i,j}^\text{Str-SNc}(t) \cdot u_j^\text{Str}(t) + \text{DA}_\text{base} \text{DA}i(t)=(m_i^\text{DA}(t))^+
Reward R(t) is set to 0.5 when received and to 0.0 otherwise; when above zero, R(t) decreases by one-thousandth of its value at each time step. The timing factor of reward prediction P(t) is set to 1.0 when reward is expected and to 0.0 else. For the time constant \tau we chose a relatively small value of 10 ms to set only a small temporal delay between reward-related events (i.e. rewards and their omissions) and changes in SNc firing (that then cause phasic changes in dopamine levels). Thereby, we ensure that the time period where reward-related events (i.e. via dopamine) are associated to neuronal eligibility traces (d\text{Ca}_{i,j}^\text{post}(t)) is temporally close to when these events take place. Larger values of \tau would result in eligibility traces decaying further before dopamine levels rise. This would result in smaller weight changes per trial and would thereby slow down learning of WM control and response selection. Furthermore, much larger values of \tau could be problematic in case of short inter-trial-intervals since reward-related events could then be associated to future (instead of previous) eligibility traces.
Learnable, negatively weighted striato-nigral afferents encode reward prediction. Depending on the balance between actual reward and reward prediction, firing rates above or below the baseline level (\text{DA}_\text{base}) of 0.5 can result. Striato-nigral weights (w_{i,j}^\text{Str-SNc}(t)) encoding reward prediction are learned via
\eta \cdot \frac{d w_{i,j}^\text{Str-SNc}(t)}{dt} = - (u_j^\text{Str}(t) - \overline{\text{Str}}(t) ) + f_\text{DA}(\text{DA}_i(t) - \text{DA}_\text{base})
The postsynaptic and the dopaminergic term are identical in this equation, resulting in a two-factor “Hebbian” learning rule.
Relationship between motor activity and overt responses
To account for imprecision in the motor command system, response selection is assumed to be based upon brain activity in a probabilistic way: The higher the activity of a particular MI cell, the greater the probability of the associated response. In case of equal activity among motor cells, the probability of each response is the inverse of the number of possible alternatives. The probability of response R_i is therefore given by
P(R_i) = 0.5 + u_i - u_j
where u_i is the firing rate of the cell associated to the response R_i and u_j the firing rate of the respective other MI cell. Probability values are reasonably restricted to the interval [0, 1].
Appendix B. Number of simulated cells
Table 4.1 presents the numbers of cells in each of the model’s layers. The two prefrontal loops each contain eight cells within lPFC, STN, GPe and GPi so that each of the 1-2-AX task’s stimuli can in principle become represented within at least one cell. MI contains two cells: one for each response. The number of striatal cells has to be considerably larger since clusters of striatal cells become receptive to various combinations of cortical afferents. The motor part of striatum exceeds the prefrontal part in size as cells from all cortical areas have to converge there.
| Cell type | Prefrontal loop | Motor loop | Visual |
|---|---|---|---|
| Cortex | 8 | 2 | 8 |
| Striatum | 25 | 49 | 0 |
| STN | 8 | 0 | 0 |
| GPe | 8 | 0 | 0 |
| GPi | 8 | 2 | 0 |
| Thalamus | 8 | 2 | 0 |
| SNc | 1 | 1 | 0 |
Appendix C. Overview of model parameters
To allow for an easy overview and comparison of the model’s parameters, these are systematically listed in Table 4.2 and Table 4.3. Table 4.2 contains the parameters for computing membrane potentials and firing rates, Table 4.3 the parameters for computing weights.
| Cell type | \tau (ms) | w^\text{ff} | w^\text{ff} | w^\text{ff} | w^\text{lat} | M | \epsilon |
|---|---|---|---|---|---|---|---|
| Cx | 5 | w^\text{Thal-Cx}: 1.0^a | w^\text{Cx-Cx}: 0.0^a | - | - | 0.0 | [-0.05; 0.05] |
| Str | 10 | w^\text{Cx-Str}: l | - | - | w^\text{Str-Str}: -0.3 | 0.3 | [-0.1; 0.1] |
| STN | 10 | w^\text{Cx-STN}: l | - | - | - | 0.0 | [-0.01; 0.01] |
| GPe | 50 | w^\text{STN-GPe}: 1.0 | - | - | - | 0.0 | [-0.1; 0.1] |
| GPi | 10 | w^\text{Str-GPi}: l | w^\text{STN-GPi}: 8.0 | w^\text{GPe-GPi}: -8.0 | w^\text{GPi-GPi}: 1.0^a | 0.8 | [-0.75; 0.75] |
| Thal | 5 | w^\text{Cx-Thal}: 0.5^a | w^\text{GPi-Thal}:-1.0 | - | - | 0.7 | [-0.1; 0.1] |
| SNc | 10 | w^\text{Str-SNc}: l | - | - | - | 0.5 | 0.0 |
| Connection type | \eta (ms) | \tau_\alpha (ms) | \gamma | \varphi | \eta^\text{inc} (ms) | \eta^\text{dec} (ms) | u^\text{MAX} | \beta | K_\alpha |
|---|---|---|---|---|---|---|---|---|---|
| w^\text{Cx-Cx} | 800 | 20 | 0.0 | - | - | - | 1.0 | - | 10 |
| w^\text{Thal-Cx} | 450 | 20 | 0.25 | - | - | - | 1.0 | - | 10 |
| w^\text{Cx-Str} | 250 | 20 | 0.55; 0.4 | 0.5; 0.1 | 1 | 500 | 1.0 | - | 10 |
| w^\text{Cx-STN} | 250 | 20 | - | 0.2 | 1 | 500 | 1.0 | - | 1 |
| w^\text{Str-GPi} | 500 | 2 | - | 10.0; 0.2 | 1 | 250 | - | 0.03; 1.0 | - |
| w^\text{GPi-GPi} | 100 | 2 | - | - | 1 | 250 | 1.0 | 0.06 | 1 |
| w^\text{Cx-Thal} | 700 | 20 | 0.1 | - | - | - | 0.8 | - | 10 |
| w^\text{Str-SNc} | 10000 | - | - | 5.0 | - | - | - | - | - |
