2 Sustained activities and retrieval in a computational model of perirhinal cortex
Abstract
Perirhinal cortex is involved in object recognition and novelty detection, but also in multimodal integration, reward association and visual working memory. We propose a computational model that focuses on the role of perirhinal cortex in working memory, particularly with respect to sustained activities and memory retrieval. This model describes how different partial informations are integrated into assemblies of neurons that represent the identity of an object. Through dopaminergic modulation, the resulting clusters can retrieve the global information with recurrent interactions between neurons. Dopamine leads to sustained activities after stimulus disappearance that form the basis of the involvement of perirhinal cortex in visual working memory processes. The information carried by a cluster can also be retrieved by a partial thalamic or prefrontal stimulation. Thus, we suggest that areas involved in planning and memory coordination encode a pointer to access the detailed information encoded in associative cortex such as perirhinal cortex.
2.1 Introduction
Perirhinal cortex (PRh), composed of cortical areas 35 and 36, is located in the ventromedial part of the temporal lobe. It receives its major inputs from areas TE and TEO of inferotemporal cortex, as well as from entorhinal cortex (ERh), parahippocampal cortex, insular cortex and orbitofrontal cortex (Suzuki and Amaral, 1994). As part of the medial temporal lobe system (with hippocampus and ERh), its primary role is considered to be object-recognition memory, as shown by impairements in delayed matching-to-sample (DMS) or delayed nonmatching-to-sample (DNMS) tasks following PRh cooling or removal (Buffalo et al., 1998; Horel et al., 1987; Meunier et al., 1993; Zola-Morgan et al., 1989). It is thought to be particularly involved in the representation and learning of novel objects (Brown and Xiang, 1998; Pihlajamäki et al., 2003; Wan et al., 1999), with a greater activation for these objects than for familiar ones. suggest that novel objects do not have a strong preexisting representation in inferotemporal cortex, and traces of long-term memory in PRh could be used to manipulate these objects.
Despite the huge amount of evidence for a mnemonic role of PRh, some recent findings suggest that it is also involved in high-level perception (for a controversy, see and ), such as object categorization and multimodal integration, by integrating different sources of information about the identity of an object Taylor et al. (2006). PRh indeed receives connections from insular cortex (somatosensory information) and the dorsal bank of the superior temporal sulcus (vision/audition coordination), therefore being at a central place for integrating different modalities of an object. Interestingly, monkeys with lesions of PRh are unable to select a visible object first sampled by touch Goulet and Murray (2001) or by a partial view of that object Murray et al. (1993).
Accordingly, PRh is neither a purely mnemonic nor a perceptual area: it is a multimodal area which is presumably involved in the goal-directed guidance of perception. This link to the goals of the task at hand is reflected by the modulation of PRh activity by reward association (Mogami and Tanaka, 2006), which strongly depends on D2 dopamine receptors (Liu et al., 2004). Also, PRh is involved in visual working memory, which is known to use integrated representations of objects rather than individual features (Lee and Chun, 2001; Luck and Vogel, 1997). showed that PRh cells are more active during a DMS task when their preferred stimulus is the sample (the object to be remembered) than when it is the match (the target) and that this property is actively reset between trials, supporting the evidence of a higher cognitive involvement. Some PRh cells also exhibit sustained activity between sample and match: their proportion has been estimated to 35% compared to 22% in IT or 71% in ERh (Nakamura and Kubota, 1995; Naya et al., 2003). However, contrary to ERh, these sustained activities are not robust to the presentation of distractors between sample and match (Miller et al., 1993b; Suzuki et al., 1997). The exact mechanism and purpose of these sustained activities is still unknown. Are they only provoked by feedback connections from prefrontal cortex where sustained activities are robust to distractors (Miller et al., 1996), or does prefrontal cortex just control the maintenance or suppression of these sustained representations that are created with intrinsic mechanisms in PRh?
This article presents a computational model of PRh focused on the involvement of this cortical area in visual working memory processes, by emphasizing the effect of dopamine modulation on perirhinal cell activation. Our aim is neither to model every aspect of PRh functioning nor to explore the biophysical properties of sustained activation. We rather propose a new interpretation at the functional level of these sustained activities in the framework of multimodal object identification or categorization. The model demonstrates how different aspects of an object or a category are linked into a neural assembly according to their cooccurence through time and how this assembly can be reactivated for memory retrieval.
2.2 Methods
2.2.1 Context
There are only few computational models of PRh. One of the most famous is the perceptual-mnemonic feature conjunction (PMFC) model by Bussey, Saksida and colleagues (Bussey and Saksida, 2002; Cowell et al., 2006). As its name indicates, it is primarily concerned with the interplay of perceptual and mnemonic processes in PRh. PRh is represented by a feature-conjunction layer that integrates individual features and learns to represent effectively objects in concurrent discrimination or configural learning tasks. Learning occurs either through a Rescorla-Wagner rule (Bussey and Saksida, 2002) or through self-association in Kohonen maps (Cowell et al., 2006). Despite its good predictions about the effects of PRh lesions on discrimination and configural learning tasks, it is a purely static model that can not deal with sustained activities. The model by is much more detailed and dynamic (spiking neurons) but only deals with familiarity discrimination: its Hopfield-like structure makes it able to tell rapidly if an object has already been seen but it does not allow to recollect its details. It is a purely mnemonic view of PRh. The model we propose is original with regards to the functions it describes (autoassociative memory, sustained activation, memory retrieval) and its dynamical structure.
2.2.2 Architecture of the model
To keep the model as simple as possible, we do not consider the precise timing of spikes but use mean-rate artificial neurons whose activity is ruled by a dynamical differential equation. This positive scalar activity represents the instantaneous firing rate, which is directly derived through a transfer function from the membrane potential, without using a spike-generation mechanism. As a consequence, the neurons used in this model exchange only this time-varying scalar activity through their connections, similar to dynamical neural fields (Amari, 1977; Taylor, 1999).
The neural network (Figure 2.1 - a) is composed of a population of excitatory pyramidal cells interconnected with a population of inhibitory interneurons. In order to reflect approximately the relative number of GABAergic interneurons in the cerebral cortex, the excitatory population is four times bigger that the inhibitory one Beaulieu (1993). Each inhibitory cell receives excitatory inputs from a subset of excitatory cells, with a gaussian connectivity kernel centered on the corresponding neural location. Reciprocally, each excitatory cell receives connections from a subset of inhibitory cells with a broader gaussian connectivity kernel. Additionnally, inhibitory cells are reciprocally connected with each other in a all-to-all manner, with the connection strength decreasing with the distance between cells. Excitatory cells are also reciprocally connected in an all-to-all manner, but the strength of these connections is modifiable with experience.
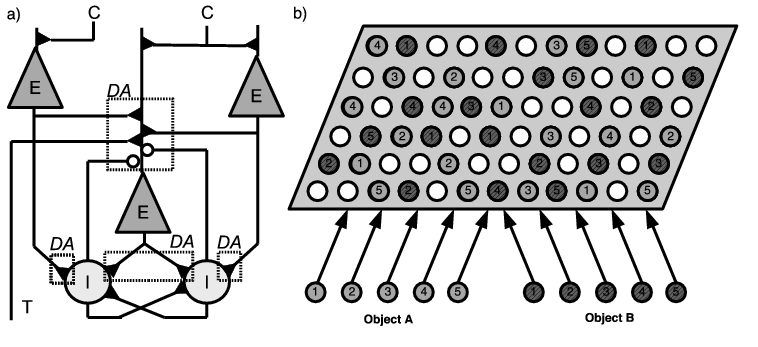
Each excitatory cell receives a cortical input that could originate in a visual area like TE or in the multimodal parahippocampal cortex. showed that neighbouring cells in PRh tend to represent the same objects after visual experience. This finding could be explained by a self-organization of receptive fields, i.e. the modification of feedforward connections. Our model does not include this feed-forward learning but is rather designed to show how the gathering of these different informations can occur in PRh. The cortical input to a cell will therefore be a time-varying scalar value, reflecting the weighted sum of the activity of its afferent cells, without any information about its origin. The basic idea of the model is that the perirhinal neurons representing a given object or category have receptive fields selective for a particular aspect of that object or category, either in visual space (different views of an object or different exemplars of a category sharing some visual features) or in multimodal space (some neurons are preferentially activated by the sound associated to this object, or its touch). In the following, we will not distinguish between the learning of different views or modalities of an object, or the learning of a category represented by different exemplars: the mechanism remains the same and we will use the term “object” for either a real object or a category. The increase in the strength of the lateral reciprocal connections between excitatory cells will provoke a clustering effect: the representation of an object will be distributed over several cells (forming what is called a cluster or an autoassociative pattern) which are individually selective for a particular aspect.
In our simulations, an object is represented by five parts corresponding each to a particular aspect. Each part provides a cortical input to four excitatory cells in PRh (randomly chosen in the population), meaning that the representation of all aspects of an object forms a cluster of twenty neurons (Figure 2.1 - b). During learning, each object will be successively presented during a certain amount of time (250 ms here), but each of its parts will be randomly active with a probability of 0.6. The random activation of parts means that each presentation of an object will be incomplete in most cases. The goal of the learning in the lateral connections will be to correlate the different parts, even if they do not constantly appear together. Unless stated otherwise, all the simulations have been done with two different objects.
2.2.3 Dopamine modulation
Dopamine (DA) modulation is a very important feature of the model, responsible for most of its interesting properties. Unfortunately, little is known about its effects in PRh. We will therefore assume that dopamine modulation in PRh is similar to what occurs in prefrontal cortex, given the fact that PRh has a similar ratio of D1/D2 receptors, even if their density is higher (Hurd et al., 2001). An exhaustive review about dopamine effects on prefrontal cells can be found in . The picture that emerges from experimental observations is very heterogeneous. However, there is some accumulating evidence for the following properties:
- the effect of DA is strictly modulatory: it does not induce excitatory post-synaptic currents by itself (Yang and Seamans, 1996);
- DA modulates both pyramidal and fast-spiking inhibitory interneurons (Gorelova et al., 2002);
- DA modifies the cell’s excitability by modulating intrinsic ionic currents like \text{Na}^{+} and \text{K}^{+} (Yang and Seamans, 1996);
- the effect of DA is dose-dependent: D1 receptor activation can have opposing functional effects depending on the level of stimulation, following an inverted U-shape (Goldman-Rakic et al., 2000);
- the effect of DA is neurotransmitter receptor-dependent: NMDA- (excitatory activity-dependent) and GABA- (inhibitory) mediated currents are enhanced by DA, but AMPA- (excitatory) mediated ones are decreased (Cepeda et al., 1992; Momiyama et al., 1996);
- the effect of DA is dendrite-dependent: DA reduces more strongly the EPSPs generated in apical dendrites (long-distance cortical inputs) than in the basal ones (neighbouring pyramidal cells), through a reduction of dendritic \text{Ca}^{2+} currents (Yang and Seamans, 1996; Zahrt et al., 1997);
- the effect of DA is activity-dependent: the more the cell is active, the more DA modulates its inputs (Calabresi et al., 1987);
- DA levels are long-lasting in the target area Huang and Kandel (1995). The phasic DA bursts in the dopaminergic cells are therefore not relevant: we will only consider the tonic component of DA activity, not its phasic component.
Existing models of dopaminergic modulation of sustained activies in prefrontal cortex do not all make the same hypothesis about the exact influence of DA. A detailed model by supposes that DA enhances the persistent \text{Na}^{+} ionic currents, reduces the slowly inactivating \text{K}^{+} ionic currents, reduces the efficiency of apical inputs, reduces the amplitude of glutamate-induced EPSPs (including NMDA, even if they admit this is controversial) and increases the spontaneous activity of GABAergic cells as well as the amplitude of IPSPs in pyramidal cells. In their respective models, as well as suppose that DA only enhances NMDA-mediated currents in the basal dendrites in coordination with a simultaneous increase of the amplitude of IPSPs. On the contrary, consider that DA momentarily restricts excitatory inputs on apical dendrites. More recently, considered that DA only modifies the gain of cells by increasing their firing threshold, without being more specific about synaptic currents.
The major link between most of these models is that they distinguish the effects of DA on apical dendrites and on basal dendrites of pyramidal cells: the influence of long-distance cortical inputs is reduced by DA whereas the influence of neighbouring pyramidal cells is increased. This last assumtion is coherent with the fact that basal dendrites are primarily NMDA-mediated (Schiller et al., 2000). The reduction of apical currents allows the network to be momentarily insensitive to external inputs, increasing the robustness of sustained activities when they appear. In the case of PRh, as we know that sustained activities are not robust to the appearance of distractors (Miller et al., 1993a), we neglected this effect. Accordingly, the major influences of DA we consider in our model are therefore the increase of the efficiency of lateral connections between excitatory cells (on an activity-dependent manner, as they are mainly mediated by NMDA receptors), the increase of the amplitude of IPSPs (by increasing the efficiency of the connections from inhibitory to excitatory cells) and the increase of the activity of the inhibitory cells through an increase in the efficiency of the connections from excitatory to inhibitory cells. These assumptions are summarized in Figure 2.1 - a. The modification of the excitability of cells through modulation of ionic currents has not been taken into account since the effects of this mechanism are thought to be similar to the selective modulation of synaptic currents. The differential effects of D1-like and D2-like receptors have not been considered since there exists no sufficient experimental evidence to draw a precise line between them.
2.2.4 Equations for updating the activity
The model consists of a single map of N \times N excitatory units and \frac{N}{2} \times \frac{N}{2} inhibitory units. We use N = 20 for the results in this paper, but the properties of the model do not depend on this particular size: it has been tested from N=10 to N=40, showing that distributed computations and flexible learning can induce scalability. We used a mean-field approach, where the activity of each unit follows an ordinary differential equation, discretized with a timestep of 1 ms. In the mean-field approach, a unit represents a population average of a certain number of single cells. Since the true underlying circuitry is not well known, we do not explicitely derive the mean-field solution but describe the dynamics at the macroscopic population level. Nevertheless, for the sake of simplicty, we use the term “cell” for a unit. The mean activity I_i (t) of an inhibitory cell at time t is ruled by Equation 2.1:
\tau_I \cdot \frac{d I_i (t)}{d t} + I_i (t) = \sum_{j \neq i} W^{II}_{i j} \cdot I_j (t) + ( 1 + K^{EI} \cdot DA ) \times \sum_{k} W^{EI}_{i k} \cdot E_k (t) +\eta^I_i (t) \tag{2.1}
where \tau_I = 10 ms is the net time constant of the unit. W^{II} is the set of connections between inhibitory cells, decreasing with the distance between the cells and W^{EI} is the set of connections from the excitatory cells (activity denoted E_k (t)) to the inhibitory cell (formulas given in the appendix). The dopamine level in the network (represented by the scalar value DA between 0 and 1) increases the gain of inputs from excitatory cells. K^{EI} is a fixed scaling parameter. Finally, \eta^I (t) is a noise added to the cell that randomly fluctuates in the range [- 0.1, 0.1]. The resulting activity is restricted to positive values.
The mean activity E_i (t) of an excitatory cell at time t is ruled by Equation 2.2:
\begin{aligned} \tau_E \cdot \frac{d E_i (t)}{d t} + E_i (t) = f ( & ( 1 + K^{EE} \cdot \sigma^{lat}(DA) \cdot \sigma^{EE} (E_i (t)) ) \cdot \sum_{j \neq i} W^{EE}_{i j} \cdot E_j (t) \\ + &( 1 + K^{IE} \cdot \sigma^{GABA} (DA) \cdot E_i^2 (t)) \cdot \sum_k W^{IE}_{i k} \cdot I_k (t) \\ + & W^{C}_i \cdot C_i (t) \\ + & (1 + K^{T} \cdot \sigma^{T} (DA) ) \cdot T_i (t) \\ + & \eta^E_i (t) ) \end{aligned} \tag{2.2}
where \tau_E = 20 ms is the net time constant of the unit. This value is chosen twice as large as in the inhibitory units to reflect the ratio of membrane time constants between pyramidal cells and inhibitory interneurons in the cortex (McCormick et al., 1985). f (x) is a transfer function, ensuring that the activity of the cell does not reach too high values. It is linear in the range [0, 1] and then saturates slowly to a maximum value of 1.5 (formula given in the appendix). There are five terms inside this transfer function. The first term denotes the influence of the lateral connections between excitatory cells W^{EE}. Its gain depends on dopamine through a sigmoidal term \sigma^{lat} and a fixed scaling parameter K^{EE} but also on the activity of the cell itself through another sigmoidal function \sigma^{EE}. For these predominantly NMDA-mediated lateral connections, the influence of DA is therefore activity-dependent. These two sigmoids are independent to ensure that DA only modulates active cells and that effective transmission of activity through NMDA-mediated connections between excitatory cells only occurs in the presence of DA. The second term represents the influence of the connections from the inhibitory cells with a negative strength W^{IE}. Their efficiency also increases with dopamine (sigmoidal function \sigma^{GABA} and fixed scaling parameter K^{IE}) and the activity of the cell. The feedforward inhibition produced by the increase of the efficiency of IPSPs by high levels of DA on pyramidal cells, as proposed by , is realized through a square of the activity of the cell itself. The third term is the contribution of the cortical input C_i (t) through a random weight W^{C}_i, without any dopaminergic modulation since they are considered to reach apical dendrites (see the Dopamine modulation section). When the cell is stimulated, we set C_i(t) = 1.0. The fourth term is the contribution of a possible thalamic input T_i (t), increased by dopamine through \sigma^{T} and the scaling parameter K^{T}. This term is clearly distinct from the cortical inputs: although PRh is dysgranular - with a very thin layer IV (Rempel-Clower and Barbas, 2000) - thalamocortical afferents from the dorsal and medial geniculate nuclei target layers I, III/IV and VI (Furtak et al., 2007; Linke and Schwegler, 2000), therefore on both apical and basal dendrites of pyramidal cells, as well as on various interneurons. We therefore assume that the thalamic input has a driving force through apical dendrites, similar to the cortical input, and a dependence on dopamine through the basal dendrites. The last term \eta^E (t) is a noise randomly fluctuating in [- 0.5, 0.5]. The resulting activity is restricted to positive values. Details about the sigmoidal functions and other parameters are given in the appendix.
While the general properties of DA modulation are largely supported by the discussed observations, the exact parameters and sigmoid functions have been determined through trial-and-error processes to enable sustained activities. Although the results we present here quantitatively depend on these choices, the global properties we intend to highlight admit some variations in the values of the parameters.
2.2.5 Learning rule
The lateral reciprocal connections between excitatory cells W^{EE} are subject to learning. We considered a covariance rule combining input- and output-dependent LTP (long-term potentiation) and output-dependent only LTD (long-term depression):
\begin{aligned} \tau_W \cdot \frac{d W^{EE}_{i j} (t)}{d t} = (E_i (t) - \hat{E_i} (t))^+ \cdot ( (E_j (t) - \hat{E_j} (t) )^+ - \alpha_i (t) \cdot W^{EE}_{i j} (t) \cdot (E_i (t) - \hat{E_i} (t))^+ ) \end{aligned} \tag{2.3}
where E_i (t) is the pre-synaptic activity of cell i, E_j (t) the post-synaptic activity of cell j. ()^+ is the positive part function. \hat{E_k} (t) is a temporal sliding-mean of the activity E_k (t) over a window of T ms defined by:
\begin{aligned} \hat{E_k} (t) = \frac{(T-1) \cdot \hat{E_k} (t - 1) + E_k (t)}{T} \end{aligned} \tag{2.4}
with T = 5000 ms in this model. This term ensures that learning occurs only when pre-synaptic or post-synaptic activities are significantly higher than their baseline value, ruling out learning of noise. However, the final weights determined by this rule alone are strongly dependent on the value of the parameter \alpha_i, which is constant in classical covariance rules. If \alpha_i is set too high, weights will never increase enough to produce post-synaptic activity, but if \alpha_i is too low, the post-synaptic cell will have maximal activity for a too large set of stimuli. As we want our model to deal with different cluster sizes, we had to use a more flexible approach for the learning rule. We therefore focused on homeostatic learning, where the learning rule uses as a constraint that the activity of a cell should not exceed a certain value, in order to save energy (Rossum and Turrigiano, 2001; Turrigiano and Nelson, 2004). Homeostatic learning is possible when the parameter \alpha_i can vary with the experience of the cell, in our case when the cell’s activity exceeds a certain threshold. The following rule is used:
\begin{aligned} \tau_{\alpha} \cdot \frac{d \alpha_{i} (t)}{d t} + \alpha_i (t) = K_\alpha \cdot H_i (t) \end{aligned} \tag{2.5}
\begin{aligned} \tau_H \cdot \frac{d H_{i} (t)}{d t} + H_i (t) = K_H \cdot ( (E_i (t) - E_{max})^+ )^2 \end{aligned} \tag{2.6}
with H_i (t) and \alpha_i (t) restricted to positive values and \alpha_i (0) equal to 10.
When E_i (t) exceeds E_{max} (1.0 in our model), H_i (t) becomes rapidly highly positive, leading to a slow increase of \alpha_i (t). The inhibitory part of Equation 2.3 becomes preponderant and all the weights decrease. The reason why H_i (t) is introduced is that \alpha_i (t) must have a slow time constant so that learning is stable. This learning rule is similar to the classical BCM rule (Bienenstock et al., 1982) but is more stable, since the inhibitory term in Equation 2.3 represents a constraint both on a short time scale - by its dependance on E_i (t) and W^{EE}_{i j} (t)- and on a long time scale with \alpha_i (t). The effect of this learning rule is that weights will rapidly increase at the beginning of learning (the Hebbian part of Equation 2.3 is preponderant) but when the cells begin to overshoot, \alpha_i (t) increases and forces the cell to find a compromise between increasing its afferent weights and activity overshooting. When learning is efficient, \alpha_i (t) stabilizes to an optimal value that depends on the mean activity of the cell.
2.3 Results
We will first show the consequence of learning the lateral connections between excitatory cells on the formation of clusters and the propagation of activity within the cluster. We then demonstrate the effect of DA modulation on sustained activities in the network and show that the model follows the classical inverted-U shaped curve. After introducing these basic properties, we then demonstrate the specific properties for memory recall such as the dependence of the propagation of activity between two clusters on the strength of their reciprocal connections, as well as the effect of thalamic stimulation on memory retrieval
2.3.1 Learning and propagation of activity within a cluster
During learning, a sequence of stimuli is shown to the network. The first object is presented for 250 ms, activating a random number of parts of the corresponding cluster. No stimulation is given to the network for the next 250 ms, followed by the second object for 250 ms and further on. This sequence is repeated for 100 times. Please note that this is one particular learning protocol, but that other protocols ensuring that each objet is sufficiently often presented also work. The dopamine level is set to a low value of 0.1 during learning, for reasons explained in the Discussion section.
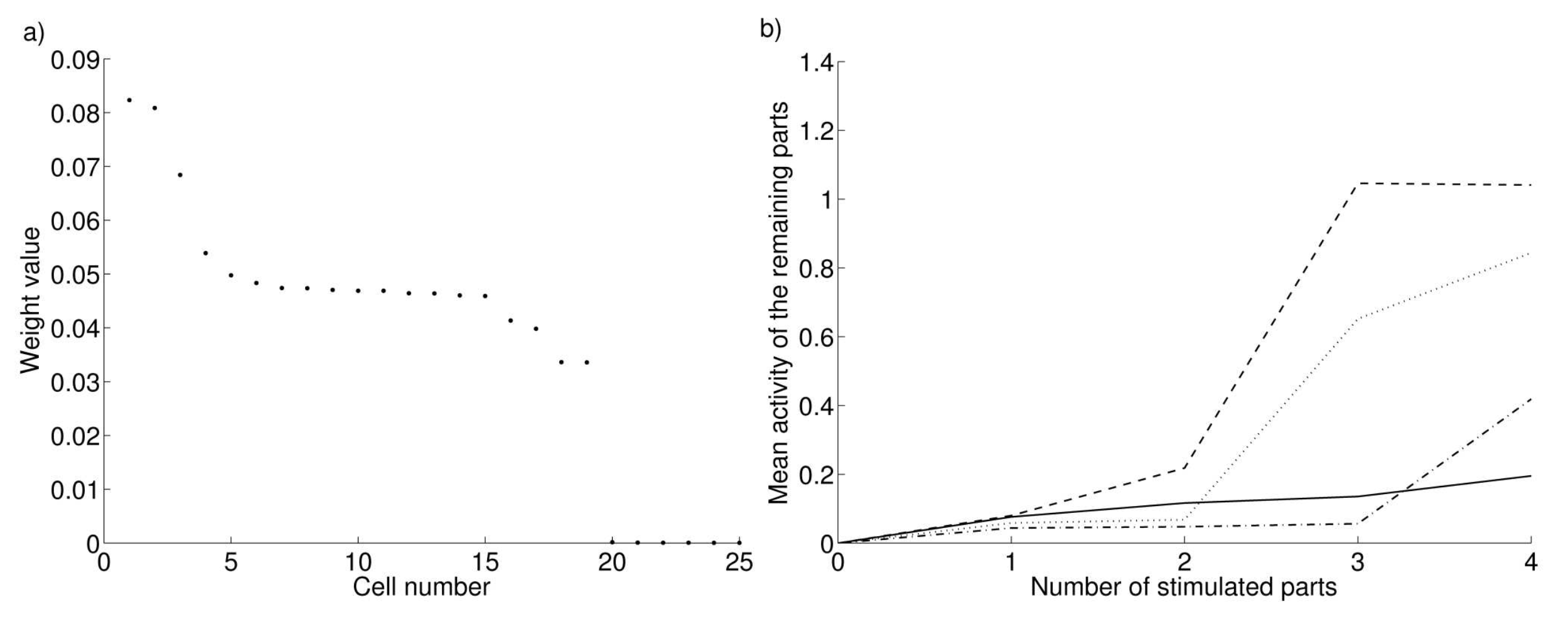
After learning, each cell has built connections with the cells representing other parts of an object. Figure 2.2 - a shows the 25 highest connection values for a randomly selected cell in the first cluster. One can observe that this cell has formed positive connections with the 19 other cells of the cluster. The weights within a cluster are not all equal, reflecting the probability of cooccurrence of the different parts during learning. Oppositely, the connections with cells of another cluster have been reduced to neglictable values.
After learning, how do we functionaly retrieve the information about the correlation between different parts? Our hypothesis is that the activation of a sufficient number of parts should provoke activity in the remaining parts, at least under certain dopamine levels. Figure 2.2 - b shows the mean activity of the remaining parts dependent on the numbers of parts that receive cortical activation. When dopamine has too low (0.2) or high (0.8) levels, the remaining parts show only little activation, even if four out of five parts are stimulated. When dopamine has an intermediate level (0.4 or 0.6) and three or more parts are activated, the remaining parts show strong activity, as if they actually received cortical input. This shows that under intermediate dopamine levels, the network is able to retrieve all the parts of a cluster if a majority of them is stimulated. We also simulated clusters of bigger size (up to 20 parts of four cells, i.e. 80 cells) and observed that this minimum proportion of stimulated parts is slightly decreasing with the cluster size, but it is always superior to one third.
2.3.2 Sustained activities and intermediate values of dopamine
In the following experiments, we stimulate only three parts of a cluster (12 cells out of 20) and record two different neurons, one belonging to these three parts and called the “stimulated” cell, the other to one of the two remaining parts and called the “unstimulated” cell.
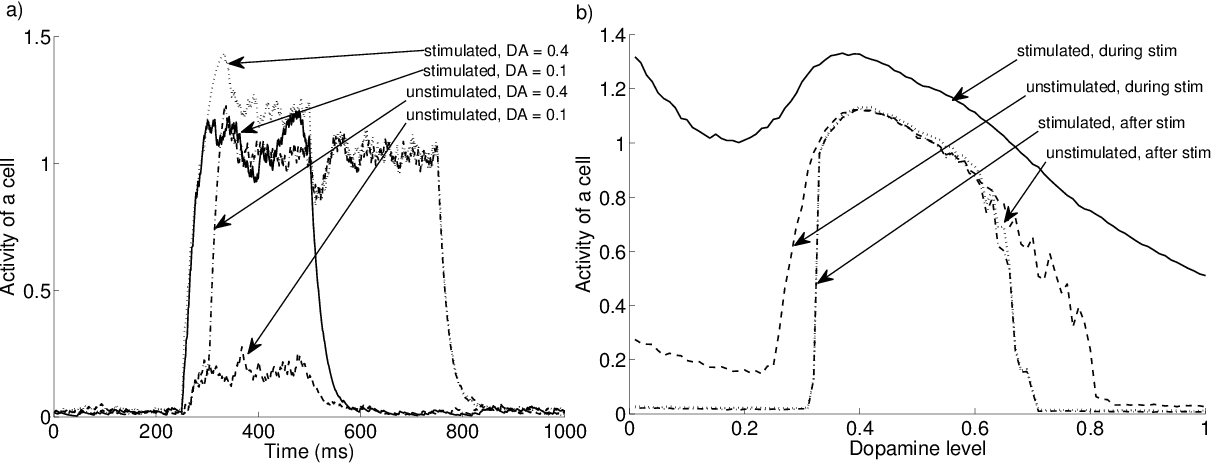
To determine the adequate range of dopamine levels, it is interesting to look at the sustained activities observable in the network. Figure 2.3 - a shows the timecourse of the activity of two cells during the successive presentation of the two objects. With a low dopamine level (0.1), only the stimulated cell shows significant activity (around 1.0) during the presentation of the object. With an intermediate dopamine level (0.4), both cells become highly active (around 1.2 and 1.0, respectively) during the stimulation, with a little timelag due to the propagation of activity within the cluster. When the stimulation ends, their activity does not fall back to baseline but stays at a high level (1.0). This sustained activity is only due to the reciprocal interactions between excitatory cells and their modulation by dopamine.
When the second object is presented, its representation competes with the sustained activation. If the two representations are equally distributed on the map, which is the case here, some of their excitatory cells will be connected to the same inhibitory cells, leading to enhanced inhibition and disruption of the sustained activities. If the two representations are spatially segregated on the map (corresponding for example to two objects from very different categories, like a face and a tree), the two representations can exist in parallel. Data from about the robustness of sustained activities in PRh does not deal with the distribution of competing stimuli on the surface of the cortex, allowing this property to be a prediction of the model. However, if the distracting stimulus has a low intensity (C_i(t) < 0.4) or is not represented by more than two parts, the sustained representation can resist its appearance, thanks to the increased activity of inhibitory cells.
Figure 2.3 - b shows the influence of the dopamine level on the activities of the two considered cells during and after stimulation. When the cluster is partly stimulated, dopamine globally enhances the activity of the stimulated cell when DA is inferior to 0.4 but then begins to depress it. For the unstimulated cell, one can observe a strong enhancing effect when dopamine is around 0.25 due to the propagation of activity within the cluster. When dopamine exceeds 0.8, the activity of this cell falls abruptly to zero, showing that propagation of activity is not possible under high levels of dopamine, because of the enhancement of the reciprocal connections between inhibitory and excitatory cells. The two lower curves of Figure 2.3 - b show the sustained activity of the two cells 100 ms after the end of the stimulation. They have an inverted-U shape which is typical for dopaminergic modulation of working memory in prefrontal cortex (Goldman-Rakic et al., 2000). The graph shows that the values of dopamine in our model that allow to observe sustained activities range between 0.3 and 0.7. The amplitude of the sustained activities is relatively high (up to 80% of the activity during stimulation depending on the dopamine level) but is coherent with cellular recordings (Curtis and D’Esposito, 2003; Naya et al., 2003; Ohbayashi et al., 2003). Due to the balanced background inhibition, we can also change the parameters of the model to obtain lower sustained activities.
2.3.3 Propagation of activity between clusters
The propagation of activity within a cluster is an interesting property in the framework of multimodal object categorisation and identification. However, contrary to the preceding experiments where the two learned objects do not share any parts, learning in the real world does not ensure that parts of two different objects are not activated at the same time in PRh, for example because these objects share these parts. Consequently, the weights between two clusters are not necessarily equal to zero. What happens to the propagation of activity if two clusters are reciprocally connected with small weight values?
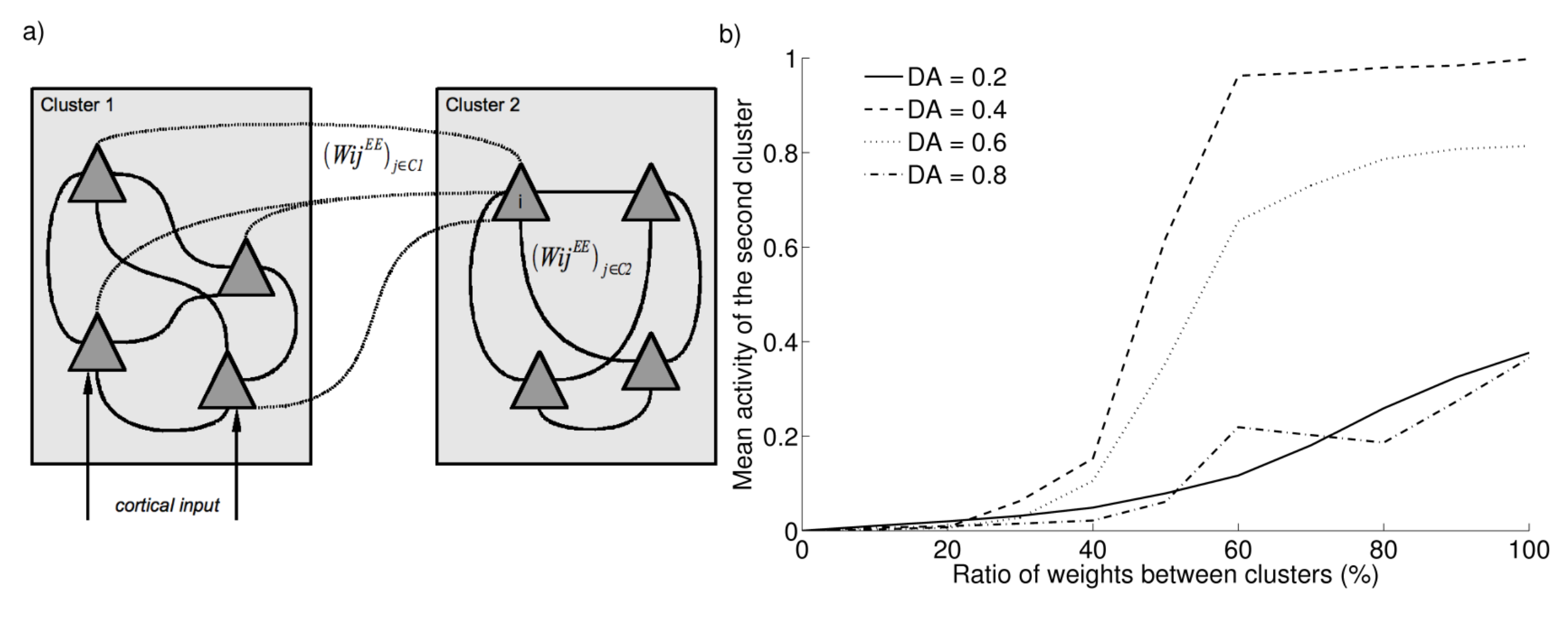
Figure 2.4 shows the influence of these inter-cluster connections. After the two clusters have been learned, we artificially increase the strength of connection between the two groups of cells. As each cell does not receive the same amount of cortical input because of the random weights W^C_i, their lateral connections W^{EE}_{i j} are not equal. We therefore computed the mean value of these lateral connections for each cell of the second cluster (called the intra-cluster connection value) and set the connections from the first cluster to the corresponding cell in the second cluster proportional to this value (inter-cluster connection value).
We then stimulate three parts of the first cluster and record the mean activity of the second cluster. Under low or high dopamine levels, inter-cluster connections can be equal to the intra-cluster connections (meaning that they form one bigger cluster) without observing any propagation of activity to the second cluster. Under intermediate dopamine levels, the ratio between these connections must be below 40% to avoid that the activation of one cluster propagates without control to other weakly connected clusters. This result ensures a reasonable trade-off between stability of object representation and propagation of activity.
2.3.4 Thalamic stimulation
The preceding results show that our model is able to learn to correlate different parts of an object through lateral connections and to propagate activity between these parts under intermediate dopamine levels. It also exhibits sustained activity after an object is presented, but which is easily disrupted by similar distractors. What can be the interest of such unrobust sustained activities in the more general framework of visual working memory? Our conviction is that this high-level representation of an object does not need to be actively maintained through time but only regenerated when needed. A cluster describes quite exhaustively the different aspects of an object: what needs to be remembered is more the location of the cluster in PRh than the details of its representation. Propagation of activity within a cluster seems a useful mechanism in the sense that external activation of parts of a cluster can be sufficient under intermediate dopamine levels to retrieve the whole information carried by the cluster. This external activation can take its origins either from prefrontal cortex or from the basal ganglia - through the dorsal nucleus of the thalamus- where sustained activities are robust.
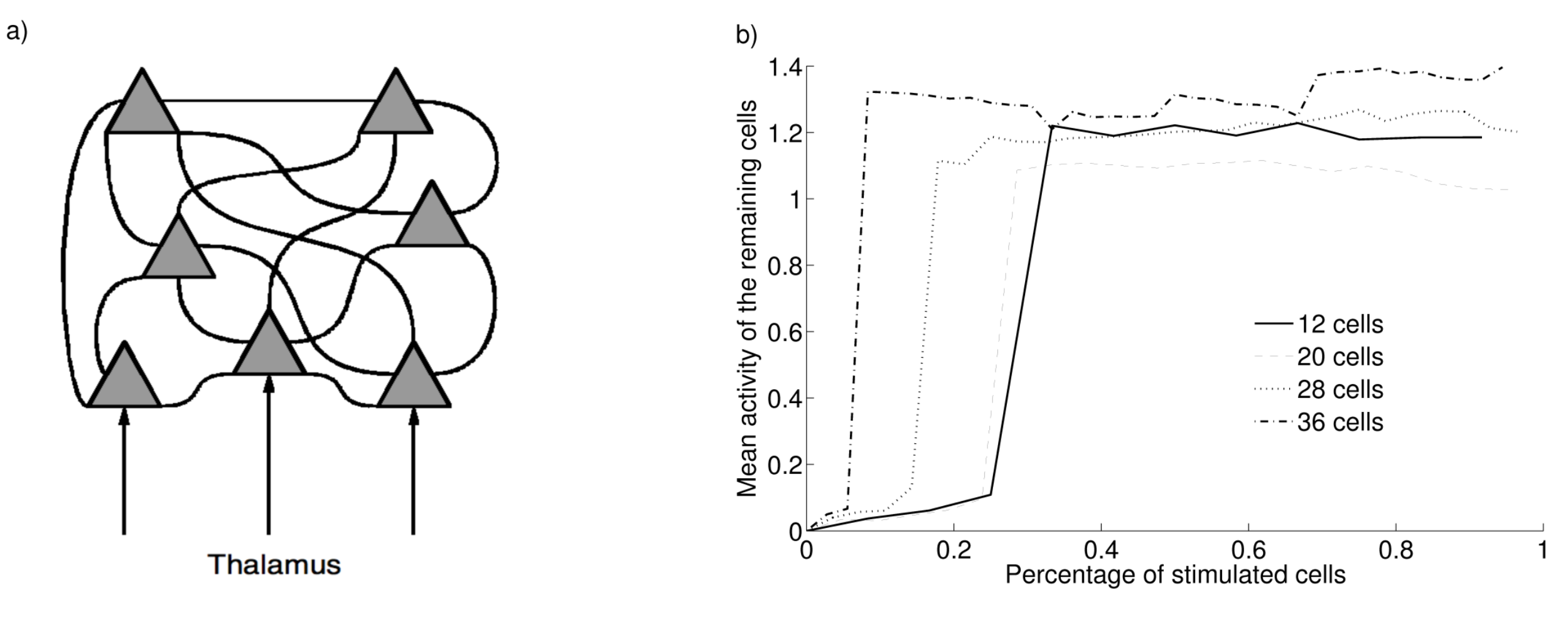
Figure 2.5 shows the influence of partial thalamic stimulation of the cells of a cluster. For this experiment, the network learned simultaneously four clusters of different sizes: 12 cells (3 parts), 20 cells (5 parts), 28 cells (7 parts) and 36 cells (9 parts). A learning cycle (the successive presentation of the four partially stimulated objects) is therefore two times longer (2 seconds) and learning is stopped after 200 cycles. For each cluster, we feed a certain percentage of cells with thalamic input (T_i = 1.0) and we record the mean activity of the remaining cells. Using an intermediate dopamine level (0.5), one can observe that, for the cluster of 12 cells, a thalamic stimulation of at least 35% of its cells is sufficient to propagate activity in the cluster. This proportion is even smaller with clusters of bigger sizes. This property allows the retrieval of the encoded information in the cluster without knowing all its details. The consequence is that a robust working memory of an object does not require to contact all the cells of a cluster but only a small portion of them, making manipulation easier and more flexible.
2.4 Discussion
The proposed computational model of PRh focuses on multimodal object representation. It learns to integrate different parts of an object, even if they do not all appear together during learning. The resulting clusters of reciprocally interconnected neurons are modulated by dopamine, so that, under an intermediate level, activation of a majority of parts propagates to the rest of the cluster and sustained activities appear after stimulus disappearance. Despite the fact that these sustained activities are not robust to distractors - as experimentally found in -, a cluster can be reactivated through thalamic stimulation of less than 35% of its cells (depending on the size of the cluster) and allows the retrieval of the global information.
The major implication of this model is that the maintenance in working memory of the visual attributes of an object is located in PRh - more precisely in the lateral connections of its cells - but that the manipulation of the content of working memory (robustness to distractors, retrieval) has to come from external regions like the thalamus or prefrontal cortex. A testable prediction is that unrobust sustained activities can be observed in PRh without any feedback from prefrontal cortex, as proposed also by or . Similarly to what is observed in prefrontal cortex (Goldman-Rakic et al., 2000), we also suggest that sustained activities in PRh have an inverted-U shape dependence with dopamine levels: no sustained activity for low or high levels of dopamine, sustained activities in the intermediate range. Cellular recordings could also reveal our “propagation of activity” property: cells that are selective for a part of an object that is not presented should respond to the object under intermediate level of DA but not under low levels. Moreover, we predict that these activations will be slightly delayed.
This model principally relies on the modulation by dopamine of various synaptic currents. Although a lot of -sometimes contradictory - data exists regarding the action of DA on prefrontal cells (Seamans and Yang, 2004), little is known about its action on PRh cells. We hypothesized that PRh cells are similarily modulated by DA, but put emphasis on different aspects. In particular, some models of sustained activation in prefrontal cortex (Dreher et al., 2002; Durstewitz et al., 1999) consider that DA primarily restricts the efficiency of cortical inputs on apical dendrites, allowing the network to be isolated from outside distractors. As sustained activities are not robust in PRh, we considered that this apical reduction was not as important as in prefrontal cortex and chose not to use it in the model. On the contrary, we considered that the main influences of DA are to enhance the NMDA-mediated currents provoked by the lateral connections from neighbouring cells and the GABA-mediated currents coming from inhibitory cells like in (Brunel and Wang, 2001; Deco and Rolls, 2003). This assumption is at the core of our model and is susceptible to be experimentally confirmed.
We focused on the tonic component of DA release by considering DA levels in PRh constant over sufficiently long periods. We are not aware of any study that investigated the effect of DA over time in PRh, but our assumption is motivated by observations in hippocampus where the effects of DA can last up to three hours (Huang and Kandel, 1995) and in prefrontal cortex (Grace, 1991) where similar observations have been made. Such long-lasting DA effects can be critical in the learning phase. Here, we set DA to a low value (0.1) since intermediate values partially impair learning: the global efficiency of excitatory lateral connections has to compensate almost exactly the global efficiency of inhibitory connections (which increases faster than the dopaminergic modulation term of excitatory connections). If the DA level is too high during learning, the afferent weights can not increase enough since the homeostatic rule impairs learning when the activity of the cell exceeds a threshold. Thus, the lateral connections will not compensate the disappearance of the cortical input: there will be no sustained activity. However, they remain strong enough to propagate activity within the cluster. Therefore, this model can not handle high constant levels of DA during the whole learning process (what would be however unrealistic), but only some increases to high levels for a finite period of time. These transient increases (which are not however phasic bursts) could momentarily signal the behavioural importance of certain objects and favorize their learning, but on the long-term DA should show habituation to these objects.
The sustained activation in this model relies on the reciprocal interactions between excitatory cells. This concept has already been used in the previously cited computational models of working memory in prefrontal cortex (Brunel and Wang, 2001; Chadderdon and Sporns, 2006; Deco and Rolls, 2003; Dreher et al., 2002; Durstewitz et al., 1999). The major differences with most of these models is that in our model these lateral connections are primarily relevant for memory recall and that they adapt to the experience of the system so that the attractors of the network can evolve through time. Another remarkable property is that the cells of a cluster do not need to receive input at the same time: a partial activation is enough to propagate activity and to create sustained activities in the whole cluster. It could be possible that the sustained activities in PRh have no direct purpose but they occur as a side effect of the propagation of activity for memory retrieval.
What do the clusters of cells in PRh exactly represent? We used the term “object” in a very broad sense, as a collection of parts that frequently appear together during learning. This could relate to spatial arrangements of parts of an object (the back, the seat and the feet of a chair, for example) that do not all appear at the same time depending on the point of view to the object, but partly view-invariant cells are already present in IT (Booth and Rolls, 1998). However, When PRh is functional, learning to discriminate a set of visual objects under a certain viewpoint can be easily transfered to the same objects under another viewpoint, whereas this capacity is severely impaired without PRh (Buckley and Gaffan, 1998). Another level of abtsraction for PRh is multimodal integration, i.e. linking the visual representation of an object with its tactile information, its sound or the associated action (grasping, pushing, sitting, etc).
A cluster could also represent a subordinate-level category in the sense of: different objects sharing a sufficient number of sensory features (parts) would be represented by the same cluster. For example, a cluster could be generic for different espresso cups but not mugs, lacking the genericity of the “cup” basic-level category but providing a minimal sensory abstraction. This is coherent with the study by that indicates that PRh is only involved in fine-grained categorization. Such narrow categories could be used as “templates” to guide attention to the corresponding target through feedback connections to the ventral pathway (Hamker, 2005), as broader categories have been shown to be useless in visual search (Smith et al., 2005).
Our primary aim has been to extend the concept of visual working memory to association areas where the detailed visual properties of an object are stored. Most computational models of working memory make no such distinction and primarily deal with sustained activities in prefrontal cortex. We propose that memory retrieval is achieved through a loop between PRh, basal ganglia and thalamus. PRh receives thalamocortical connections from dorsal and medial geniculate nuclei of the thalamus and in turn projects heavily to the caudate putamen, a part of the main input structure of the basal ganglia, the striatum (Furtak et al., 2007). When a given object has to be retrieved, the basal ganglia can selectively disinhibit the thalamus and therefore favorize the thalamic stimulation of the cluster to be retrieved.
This pathway through the basal ganglia significantly compresses the information encoded in the cerebral cortex and can not represent its rich and detailed representations: as pinpoints, the number of neurons projecting to the striatum is two orders of magnitude greater than the number of striatal neurons (Kincaid et al., 1998). We propose that the basal ganglia acts as a pointer that allows to retrieve the detailed representation when necessary through the disinhibition of thalamus. Similarly, prefrontal cortex is probably not encoding the content of memory, but rather a rule to retrieve this content. In a realistic DMS task, basal ganglia and prefrontal cortex have to learn which object has to be retrieved and which should be forgotten. This work is facilitated by the fact that the exact content of a cluster in PRh does not need to be known by this external loop: stimulating 35% of its cells (or even less for bigger clusters) is sufficient to retrieve its details.
Acknowledgements
This work has been supported by the HA2630/4-1 grant of the German research foundation (Deutsche Forschungsgemeinschaft, DFG).
Appendix: details of the model
All equations described in the Materials and methods section are numerized according to the finite difference method, with a timestep of 1 ms. Their evaluation occurs asynchronously: cells are randomly evaluated and their new activity is immediately used in the rest of the computations, in order to emphasize the competition between neuronal representations (Rougier and Vitay, 2006).
The model is composed of 20 \times 20 excitatory cells and 10 \times 10 inhibitory cells. Excitatory and inhibitory cells are reciprocally connected through gaussian connectivity kernels. We thus defined a distance between cells: let the excitatory cell E_i have coordinates (x_i, y_i) \in [0..20]^2 on the map and the inhibitory cell I_j have coordinates (x_j, y_j) \in [0..10]^2. The distance d_{EI}(i, j) between the two cells is therefore given by:
d_{EI}(i, j) = \sqrt{(x_i - 2\times x_j)^2 + (y_i - 2\times y_j)^2}
Similarly, the distance d_{II}(i, j) between two inhibitory cells I_i with coordinates (x_i, y_i) \in [0..10]^2 and I_j with coordinates (x_j, y_j) \in [0..10]^2 is given by:
d_{II}(i, j) = \sqrt{(x_i - x_j)^2 + (y_i - y_j)^2}
We then define the gaussian connectivity kernels by:
W^{IE}(i, j) = -0.12 \times \exp{ \left(- (\frac{d_{EI}(i, j)}{2.5})^2 \right)}
W^{EI}(i, j) = 0.3 \times \exp{ \left( - (\frac{d_{EI}(i, j)}{2})^2 \right)}
The connections between two inhibitory cells are given by:
W^{II}(i, j) = \begin{cases} 0.02 \times \exp{ \left(- (\frac{d_{II}(i, j)}{5})^2 \right)} & \text{if } i \neq j \\ 0 & else. \end{cases}
The parameters of Equation 2.1 are the same for each inhibitory cell: \tau_I = 10 ms, K^{EI} = 1.2 and \eta^I_i (t) is a random value uniformly distributed between -0.1 and 0.1. The parameters of Equation 2.2 are: \tau_E = 20 ms, K^{EE} = 3.0, K^{IE} = 3.0, K^{T} = 1.0 and \eta^E_i (t) a random value uniformly distributed between -0.5 and 0.5. Cortical weights W^C are randomly chosen in the range [0.8, 1.2]. The sigmoidal functions \sigma^{lat}(x), \sigma^{EE}(x), \sigma^{GABA}(x), \sigma^{T}(x) all have the same shape:
\sigma(x) = \frac{1}{1+\exp{(-l \cdot (x-c))}} - \frac{1}{1+\exp{(l \cdot c)}}
with l and c being: for \sigma^{lat}(x) c = 0.3, l = 20; for \sigma^{EE}(x) c = 0.3, l = 20; for \sigma^{GABA}(x) c = 0.5, l = 10; for \sigma^{T}(x) c = 0.5, l = 10. The transfer function f(x) is defined as follows:
f(x)= \begin{cases} 0 & \text{if $x < 0$} \\ x & \text{if $0 \leq x \leq 1$} \\ \frac{0.5}{1+\exp{(- 10.0 \cdot (x-1) )}} +0.75 & \text{if $x > 1$} \end{cases}
The parameters of Equation 2.3, Equation 2.5 and Equation 2.6 are: \tau_W = 50000 ms, \tau_\alpha = 50000 ms, K_\alpha = 100, \tau_H = 100 ms, K_H = 200, E_{max} = 1.0.
