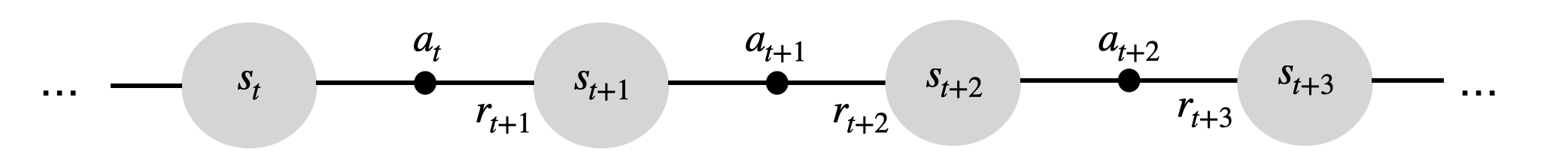Markov Decision Process
Markov Decision Process
Definition
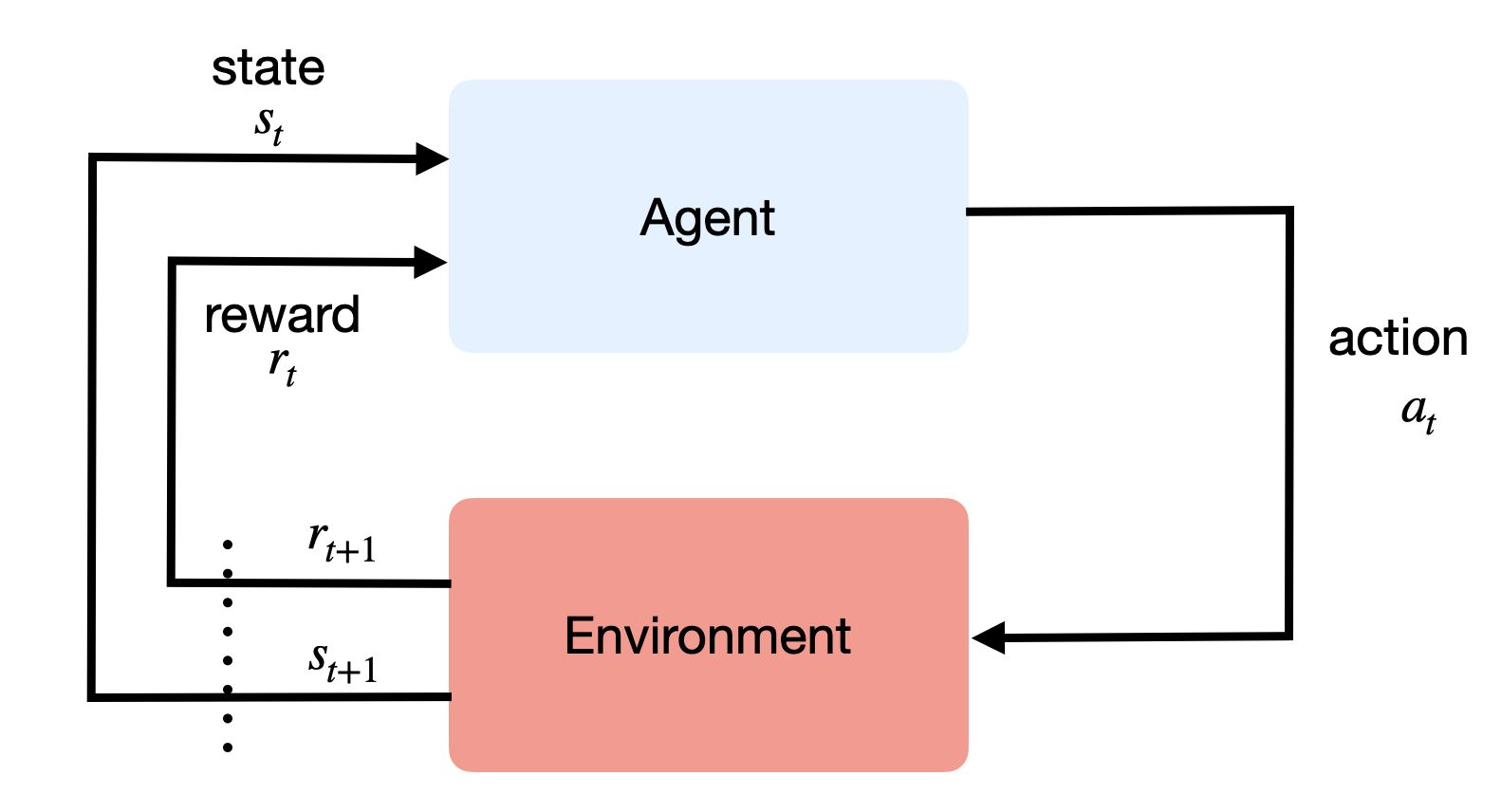
Reinforcement Learning methods apply to problems where an agent interacts with an environment in discrete time steps (Figure 3.1). At time t, the agent is in state s_t and decides to perform an action a_t. At the next time step, it arrives in the state s_{t+1} and obtains the reward r_{t+1}. In the genral case, transitions can be stochastic (there is a probability of arriving in a given state after an action), as well as the rewards (as in the bandits previously seen). The goal of the agent is to maximize the reward obtained on the long term.
These problems are formalized as Markov Decision Processes (MDP) and defined by six quantities <\mathcal{S}, \mathcal{A}, p_0, \mathcal{P}, \mathcal{R}, \gamma>. For a finite MDP, we have:
The state space \mathcal{S} = \{ s_i\}_{i=1}^N, where each state respects the Markov property.
The action space \mathcal{A} = \{ a_i\}_{i=1}^M.
An initial state distribution p_0(s_0) (from which states the agent is most likely to start).
The state transition probability function, defining the probability of arriving in the state s' at time t+1 after being in the state s and performing the action a at time t:
\begin{aligned} \mathcal{P}: \mathcal{S} \times \mathcal{A} \rightarrow & P(\mathcal{S}) \\ p(s' | s, a) & = P (s_{t+1} = s' | s_t = s, a_t = a) \\ \end{aligned}
- The expected reward function defining the (stochastic) reward obtained after performing a in state s and arriving in s':
\begin{aligned} \mathcal{R}: \mathcal{S} \times \mathcal{A} \times \mathcal{S} \rightarrow & \Re \\ r(s, a, s') &= \mathbb{E} (r_{t+1} | s_t = s, a_t = a, s_{t+1} = s') \\ \end{aligned}
- The discount factor \gamma \in [0, 1].
In deep RL, the state and action spaces can be infinite, but let’s focus on finite MDPs for now.
The behavior of the agent over time is a trajectory (also called episode, history or roll-out) \tau = (s_0, a_0, s_1, a_, \ldots, s_T, a_T) defined by the dynamics of the MDP. Each transition occurs with a probability p(s'|s, a) and provides a certain amount of reward defined by r(s, a, s'). In episodic tasks, the horizon T is finite, while in continuing tasks T is infinite.
Markov property
The state of the agent represents all the information needed to take decisions and solve the task. For a robot navigating in an environment, this may include all its sensors, its positions as tracked by a GPS, but also the relative position of all objects / persons it may interact with. For a board game, the description of the board is usually enough.
Importantly, the Markov property states that:
The future is independent of the past given the present.
In mathematical terms for a transition (s_t, a_t, s_{t+1}):
p(s_{t+1}|s_t, a_t) = p(s_{t+1}|s_t, a_t, s_{t-1}, a_{t-1}, \dots s_0, a_0)
i.e. you do not need the full history of the agent to predict where it will arrive after an action. In simple problems, this is just a question of providing enough information to the description of a state: if a transition depends on what happened in the past, just put that information in the state description.
A state representation with the Markov property should therefore not only contain all the important information available at time t, but also information from the past that is necessary to take a decision.
If the Markov property is not met, RL methods may not converge (or poorly). In many problems, one does not have access to the true states of the agent, but one can only indirectly observe them. For example, in a video game, the true state is defined by a couple of variables: coordinates (x, y) of the two players, position of the ball, speed, etc. However, in Atari games all you have access to are the raw pixels: sometimes the ball may be hidden behind a wall or a tree, but it still exists in the state space. Speed information is also not observable in a single frame.
In a Partially Observable Markov Decision Process (POMDP), observations o_t come from a space \mathcal{O} and are linked to underlying states using the density function p(o_t| s_t). Observations are usually not Markov, so the full history of observations h_t = (o_0, a_0, \dots o_t, a_t) is needed to solve the problem. We will see later how recurrent neural networks can help with POMDPs.
Rewards and returns
As with n-armed bandits, we only care about the expected reward received during a transition s \rightarrow s' (on average), but the actual reward received r_{t+1} may vary around the expected value with some unknown variance. In hard RL, we only care about the expected reward and ignore its variance, as we suppose that we can take actions an infinity of times. However, distributional RL investigates the role of this variance (see Section Categorical DQN).
r(s, a, s') = \mathbb{E} (r_{t+1} | s_t = s, a_t = a, s_{t+1} = s')
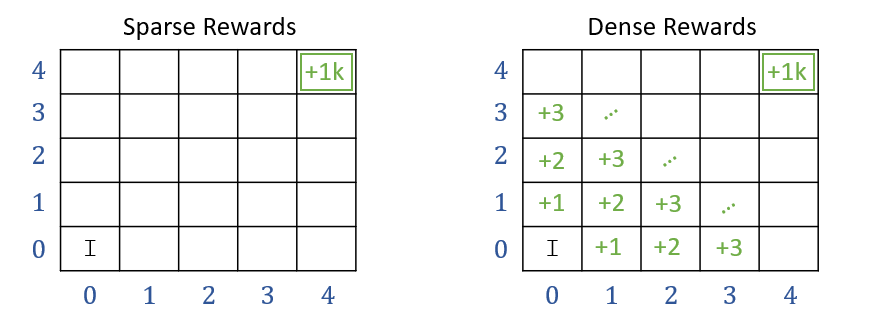
An important distinction in practice is between sparse vs. dense rewards. Sparse rewards take non-zero values only during certain transitions: game won/lost, goal achieved, timeout, etc. Dense rewards provide non-zero values during each transition: distance to goal, energy consumption, speed of the robot, etc. As we will see later, MDPs with sparse rewards are much harder to learn.
Over time, the MDP will be in a sequence of states (possibly infinite):
s_0 \rightarrow s_1 \rightarrow s_2 \rightarrow \ldots \rightarrow s_T
and collect a sequence of rewards:
r_1 \rightarrow r_2 \rightarrow r_3 \rightarrow \ldots \rightarrow r_{T}
In a MDP, we are interested in maximizing the return R_t, i.e. the discounted sum of future rewards after the step t:
R_t = r_{t+1} + \gamma \, r_{t+2} + \gamma^2 \, r_{t+3} + \ldots = \sum_{k=0}^\infty \gamma^k \, r_{t+k+1}
The return is sometimes called the reward-to-go: how much reward will I collect from now on? Of course, you can never know the return at time t: transitions and rewards are probabilistic, so the received rewards in the future are not exactly predictable at t. R_t is therefore purely theoretical: RL is all about estimating the return.
More generally, for a trajectory (episode) \tau = (s_0, a_0, r_1, s_1, a_1, \ldots, s_T), one can define its return as:
R(\tau) = \sum_{t=0}^{T} \gamma^t \, r_{t+1}
The discount factor (or discount rate, or discount) \gamma \in [0, 1] is a very important parameter in RL: It defines the present value of future rewards. Receiving 10 euros now has a higher value than receiving 10 euros in ten years, although the reward is the same: you do not have to wait. The value of receiving a reward r after k+1 time steps is \gamma^k \, r, meaning that immediate rewards are better than delayed rewards.
\gamma determines the relative importance of future rewards for the behavior:
- if \gamma is close to 0, only the immediately available rewards will count: the agent is greedy or myopic.
- if \gamma is close to 1, even far-distance rewards will be taken into account: the agent is farsighted.
Another important property is that, when \gamma < 1, \gamma^k tends to 0 when k goes to infinity: this makes sure that the return is always finite. We can therefore try to maximize it.
R_t = r_{t+1} + \gamma \, r_{t+2} + \gamma^2 \, r_{t+3} + \ldots = \sum_{k=0}^\infty \gamma^k \, r_{t+k+1}
For episodic tasks (which break naturally into finite episodes of length T, e.g. plays of a game, trips through a maze), the return is always finite and easy to compute at the end of the episode. The discount factor can be set to 1.
R_t = \sum_{k=0}^{T} r_{t+k+1}
For continuing tasks (which can not be split into episodes), the return could become infinite if \gamma = 1. The discount factor has to be smaller than 1.
R_t = \sum_{k=0}^{\infty} \gamma^k \, r_{t+k+1}
In the MDP above, selecting the action a_1 in s_1 does not bring reward immediately (r_1 = 0) but allows to reach s_5 in the future and get a reward of 10. Selecting a_2 in s_1 brings immediately a reward of 1, but that will be all.
Depending on the value of \gamma, the optimal action might be a_1 or a_2, depending on which one brings more reward on the long term.
When selecting a_1 in s_1, the discounted return is:
R = 0 + \gamma \, 0 + \gamma^2 \, 0 + \gamma^3 \, 10 + \ldots = 10 \, \gamma^3
while it is R= 1 for the action a_2.
For high values of \gamma, 10\, \gamma^3 is higher than one, so the action a_1 is the optimal action. For small values of \gamma, 10\, \gamma^3 becomes smaller than one, and the action a_2 becomes the optimal action. The discount rate \gamma can totally change the optimal behavior of the agent, that is why it is part of the MDP definition and not just a hyperparameter.
Policy
The probability that an agent selects a particular action a in a given state s is called the policy \pi.
\begin{align} \pi &: \mathcal{S} \times \mathcal{A} \rightarrow P(\mathcal{S})\\ (s, a) &\rightarrow \pi(s, a) = P(a_t = a | s_t = s) \\ \end{align}
The policy can be deterministic (one action has a probability of 1, the others 0) or stochastic. In all cases, the sum of the probabilities in a given state must be one:
\sum_{a \in \mathcal{A}(s)} \pi(s, a) = 1
The goal of an agent is to find a policy that maximizes the sum of received rewards on the long term, i.e. the return R_t at each each time step. This policy is called the optimal policy \pi^*. It maximizes the following objective function:
\pi^* = \text{argmax} \, \mathcal{J}(\pi) = \text{argmax} \, \mathbb{E}_{\tau \sim \rho_\pi} [R(\tau)]
where \rho_\pi is the density distribution of the trajectories generated by the policy \pi.
In summary, RL is an adaptive optimal control method for Markov Decision Processes using (sparse) rewards as a partial feedback. At each time step t, the agent observes its Markov state s_t \in \mathcal{S}, produces an action a_t \in \mathcal{A}(s_t), receives a reward according to this action r_{t+1} \in \Re and updates its state: s_{t+1} \in \mathcal{S}. The agent generates trajectories \tau = (s_0, a_0, r_1, s_1, a_1, \ldots, s_T) depending on its policy \pi(s ,a). The goal is to find the optimal policy \pi^* (s, a) that maximizes in expectation the return of each possible trajectory under that policy.
Value functions
A central notion in RL is to estimate the value (or utility) of every state and action of the MDP. The state-value V^{\pi} (s) of a state s is defined as the mathematical expectation of the return when starting from that state and thereafter following the agent’s current policy \pi:
V^{\pi} (s) = \mathbb{E}_{\rho_\pi} ( R_t | s_t = s) = \mathbb{E}_{\rho_\pi} ( \sum_{k=0}^{\infty} \gamma^k r_{t+k+1} |s_t=s )
The mathematical expectation operator \mathbb{E}(\cdot) is indexed by \rho_\pi, the probability distribution of states achievable with \pi. Indeed, several trajectories are possible after the state s:
- The state transition probability function p(s' | s, a) leads to different states s', even if the same actions are taken.
- The expected reward function r(s, a, s') provides stochastic rewards, even if the transition (s, a, s') is the same.
- The policy \pi itself is stochastic.
Only rewards that are obtained using the policy \pi should be taken into account, not the complete distribution of states and rewards.
The value of a state is not intrinsic to the state itself, it depends on the policy: One could be in a state which is very close to the goal (only one action left to win the game), but if the policy is very bad, the “good” action will not be chosen and the state will have a small value.
The value of taking an action a in a state s under policy \pi is the expected return starting
Similarly, the action-value (or Q-value) for a state-action pair (s, a) under the policy \pi is defined as:
\begin{align} Q^{\pi} (s, a) & = \mathbb{E}_{\rho_\pi} ( R_t | s_t = s, a_t =a) \\ & = \mathbb{E}_{\rho_\pi} ( \sum_{k=0}^{\infty} \gamma^k r_{t+k+1} |s_t=s, a_t=a) \\ \end{align}
The Q-value of an action is sometimes called its utility: is it worth taking this action?
Bellman equations
Relationship between V and Q
The value of a state V^{\pi}(s) depends on the value Q^{\pi} (s, a) of the action that will be chosen by the policy \pi in s:
V^{\pi}(s) = \mathbb{E}_{a \sim \pi(s,a)} [Q^{\pi} (s, a)] = \sum_{a \in \mathcal{A}(s)} \pi(s, a) \, Q^{\pi} (s, a)
If the policy \pi is deterministic (the same action is chosen every time), the value of the state is the same as the value of that action (same expected return). If the policy \pi is stochastic (actions are chosen with different probabilities), the value of the state is the weighted average (i.e. expectation) of the value of the actions.
➡️ If the Q-values are known, the V-values can be found easily.
We can note that the return at time t depends on the immediate reward r_{t+1} and the return at the next time step t+1:
\begin{aligned} R_t &= r_{t+1} + \gamma \, r_{t+2} + \gamma^2 \, r_{t+3} + \dots + \gamma^k \, r_{t+k+1} + \dots \\ &= r_{t+1} + \gamma \, ( r_{t+2} + \gamma \, r_{t+3} + \dots + \gamma^{k-1} \, r_{t+k+1} + \dots) \\ &= r_{t+1} + \gamma \, R_{t+1} \\ \end{aligned}
When taking the mathematical expectation of that identity, we obtain:
\mathbb{E}_{\rho_\pi}[R_t] = r(s_t, a_t, s_{t+1}) + \gamma \, \mathbb{E}_{\rho_\pi}[R_{t+1}]
It becomes clear that the value of an action depends on the immediate reward received just after the action, as well as the value of the next state:
Q^{\pi}(s_t, a_t) = r(s_t, a_t, s_{t+1}) + \gamma \, V^{\pi} (s_{t+1})
However, this is only for a fixed (s_t, a_t, s_{t+1}) transition. Taking transition probabilities into account, one can obtain the Q-values through the equation:
Q^{\pi}(s, a) = \mathbb{E}_{s' \sim p(s'|s, a)} [ r(s, a, s') + \gamma \, V^{\pi} (s') ] = \sum_{s' \in \mathcal{S}} p(s' | s, a) \, [ r(s, a, s') + \gamma \, V^{\pi} (s') ]
The value of an action depends on:
- the states s' one can arrive after the action (with a probability p(s' | s, a)).
- the value of that state V^{\pi} (s'), weighted by \gamma as it is one step in the future.
- the reward received immediately after taking that action r(s, a, s') (as it is not included in the value of s').
➡️ If the V-values are known, the Q-values can be found easily by a 1-step look-ahead, i.e. looking at the achievable states.
Bellman equations
Putting together those two equations, a fundamental property of value functions used throughout reinforcement learning is that they satisfy a particular recursive relationship:
\begin{aligned} V^{\pi}(s) &= \sum_{a \in \mathcal{A}(s)} \pi(s, a) \, Q^{\pi} (s, a)\\ &= \sum_{a \in \mathcal{A}(s)} \pi(s, a) \, \sum_{s' \in \mathcal{S}} p(s' | s, a) \, [ r(s, a, s') + \gamma \, V^{\pi} (s') ] \end{aligned}
This equation is called the Bellman equation for V^{\pi}. It expresses the relationship between the value of a state V^\pi(s) and the value of its successors V^\pi(s'), depending on the dynamics of the MDP (p(s' | s, a) and r(s, a, s')) and the current policy \pi. The interesting property of the Bellman equation for RL is that it admits one and only one solution V^{\pi}(s).
The same recursive relationship stands for Q^{\pi}(s, a):
\begin{aligned} Q^{\pi}(s, a) &= \sum_{s' \in \mathcal{S}} p(s' | s, a) \, [ r(s, a, s') + \gamma \, V^{\pi} (s') ] \\ &= \sum_{s' \in \mathcal{S}} p(s' | s, a) \, [ r(s, a, s') + \gamma \, \sum_{a' \in \mathcal{A}(s')} \pi(s', a') \, Q^{\pi} (s', a')] \end{aligned}
which is called the Bellman equation for Q^{\pi}.
Optimal Bellman equations
The optimal policy is the policy that gathers the maximum of reward on the long term. Value functions define a partial ordering over policies:
A policy \pi is better than another policy \pi' if its expected return is greater or equal than that of \pi' for all states s.
\pi \geq \pi' \Leftrightarrow V^{\pi}(s) \geq V^{\pi'}(s) \quad \forall s \in \mathcal{S}
For a MDP, there exists at least one policy that is better than all the others: this is the optimal policy \pi^*. We note V^*(s) and Q^*(s, a) the optimal value of the different states and actions under \pi^*.
V^* (s) = \max_{\pi} V^{\pi}(s) \quad \forall s \in \mathcal{S}
Q^* (s, a) = \max_{\pi} Q^{\pi}(s, a) \quad \forall s \in \mathcal{S}, \quad \forall a \in \mathcal{A}
When the policy is optimal \pi^*, the link between the V and Q values is even easier. The V and Q values are maximal for the optimal policy: there is no better alternative.
The optimal action a^* to perform in the state s is the one with the highest optimal Q-value Q^*(s, a).
a^* = \text{argmax}_a \, Q^*(s, a)
By definition, this action will bring the maximal return when starting in s. The optimal policy is therefore greedy with respect to Q^*(s, a), i.e. deterministic.
\pi^*(s, a) = \begin{cases} 1 \; \text{if} \; a = a^* \\ 0 \; \text{otherwise.} \end{cases}
As the optimal policy is deterministic, the optimal value of a state is equal to the value of the optimal action:
V^* (s) = \max_{a \in \mathcal{A}(s)} Q^{\pi^*} (s, a)
The expected return after being in s is the same as the expected return after being in s and choosing the optimal action a^*, as this is the only action that can be taken. This allows to define the Bellman optimality equation for V^*:
V^* (s) = \max_{a \in \mathcal{A}(s)} \sum_{s' \in \mathcal{S}} p(s' | s, a) \, [ r(s, a, s') + \gamma \, V^{*} (s') ]
The same Bellman optimality equation stands for Q^*:
Q^* (s, a) = \sum_{s' \in \mathcal{S}} p(s' | s, a) \, [r(s, a, s') + \gamma \max_{a' \in \mathcal{A}(s')} Q^* (s', a') ]
The optimal value of (s, a) depends on the optimal action in the next state s'.
Dynamic programming
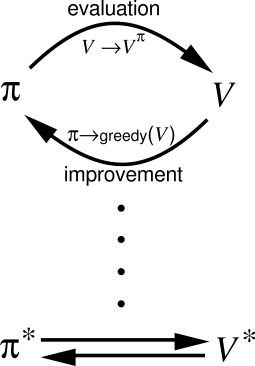
In general, RL algorithms iterate over two steps:
Policy evaluation
- For a given policy \pi, the value of all states V^\pi(s) or all state-action pairs Q^\pi(s, a) is calculated or estimated.
Policy improvement
- From the current estimated values V^\pi(s) or Q^\pi(s, a), a new better policy \pi is derived.
After enough iterations, the policy converges to the optimal policy (if the states are Markov).
This alternation between policy evaluation and policy improvement is called generalized policy iteration (GPI). One particular form of GPI is dynamic programming, where the Bellman equations are used to evaluate a policy.
Exact solution
Let’s note \mathcal{P}_{ss'}^\pi the transition probability between s and s' (dependent on the policy \pi) and \mathcal{R}_{s}^\pi the expected reward in s (also dependent):
\mathcal{P}_{ss'}^\pi = \sum_{a \in \mathcal{A}(s)} \pi(s, a) \, p(s' | s, a)
\mathcal{R}_{s}^\pi = \sum_{a \in \mathcal{A}(s)} \pi(s, a) \, \sum_{s' \in \mathcal{S}} \, p(s' | s, a) \ r(s, a, s')
The Bellman equation becomes V^{\pi} (s) = \mathcal{R}_{s}^\pi + \gamma \, \displaystyle\sum_{s' \in \mathcal{S}} \, \mathcal{P}_{ss'}^\pi \, V^{\pi} (s'). As we have a fixed policy during the evaluation, the Bellman equation is simplified.
Let’s now put the Bellman equations in a matrix-vector form.
V^{\pi} (s) = \mathcal{R}_{s}^\pi + \gamma \, \sum_{s' \in \mathcal{S}} \, \mathcal{P}_{ss'}^\pi \, V^{\pi} (s')
We first define the vector of state values \mathbf{V}^\pi:
\mathbf{V}^\pi = \begin{bmatrix} V^\pi(s_1) \\ V^\pi(s_2) \\ \vdots \\ V^\pi(s_n) \\ \end{bmatrix}
and the vector of expected reward \mathbf{R}^\pi:
\mathbf{R}^\pi = \begin{bmatrix} \mathcal{R}^\pi(s_1) \\ \mathcal{R}^\pi(s_2) \\ \vdots \\ \mathcal{R}^\pi(s_n) \\ \end{bmatrix}
The state transition matrix \mathcal{P}^\pi is defined as:
\mathcal{P}^\pi = \begin{bmatrix} \mathcal{P}_{s_1 s_1}^\pi & \mathcal{P}_{s_1 s_2}^\pi & \ldots & \mathcal{P}_{s_1 s_n}^\pi \\ \mathcal{P}_{s_2 s_1}^\pi & \mathcal{P}_{s_2 s_2}^\pi & \ldots & \mathcal{P}_{s_2 s_n}^\pi \\ \vdots & \vdots & \vdots & \vdots \\ \mathcal{P}_{s_n s_1}^\pi & \mathcal{P}_{s_n s_2}^\pi & \ldots & \mathcal{P}_{s_n s_n}^\pi \\ \end{bmatrix}
You can simply check that:
\begin{bmatrix} V^\pi(s_1) \\ V^\pi(s_2) \\ \vdots \\ V^\pi(s_n) \\ \end{bmatrix} = \begin{bmatrix} \mathcal{R}^\pi(s_1) \\ \mathcal{R}^\pi(s_2) \\ \vdots \\ \mathcal{R}^\pi(s_n) \\ \end{bmatrix} + \gamma \, \begin{bmatrix} \mathcal{P}_{s_1 s_1}^\pi & \mathcal{P}_{s_1 s_2}^\pi & \ldots & \mathcal{P}_{s_1 s_n}^\pi \\ \mathcal{P}_{s_2 s_1}^\pi & \mathcal{P}_{s_2 s_2}^\pi & \ldots & \mathcal{P}_{s_2 s_n}^\pi \\ \vdots & \vdots & \vdots & \vdots \\ \mathcal{P}_{s_n s_1}^\pi & \mathcal{P}_{s_n s_2}^\pi & \ldots & \mathcal{P}_{s_n s_n}^\pi \\ \end{bmatrix} \times \begin{bmatrix} V^\pi(s_1) \\ V^\pi(s_2) \\ \vdots \\ V^\pi(s_n) \\ \end{bmatrix}
leads to the same equations as:
V^{\pi} (s) = \mathcal{R}_{s}^\pi + \gamma \, \sum_{s' \in \mathcal{S}} \, \mathcal{P}_{ss'}^\pi \, V^{\pi} (s')
for all states s. The Bellman equations for all states s can therefore be written with a matrix-vector notation as:
\mathbf{V}^\pi = \mathbf{R}^\pi + \gamma \, \mathcal{P}^\pi \, \mathbf{V}^\pi
If we know \mathcal{P}^\pi and \mathbf{R}^\pi (dynamics of the MDP for the policy \pi), we can simply obtain the state values:
(\mathbb{I} - \gamma \, \mathcal{P}^\pi ) \times \mathbf{V}^\pi = \mathbf{R}^\pi
where \mathbb{I} is the identity matrix, what gives:
\mathbf{V}^\pi = (\mathbb{I} - \gamma \, \mathcal{P}^\pi )^{-1} \times \mathbf{R}^\pi
If we have n states, the matrix \mathcal{P}^\pi has n^2 elements. Inverting \mathbb{I} - \gamma \, \mathcal{P}^\pi requires at least \mathcal{O}(n^{2.37}) operations. Forget it if you have more than a thousand states (1000^{2.37} \approx 13 million operations). In dynamic programming, we will use iterative methods to estimate \mathbf{V}^\pi.
Policy iteration
The idea of iterative policy evaluation (IPE) is to consider a sequence of consecutive state-value functions which should converge from initially wrong estimates V_0(s) towards the real state-value function V^{\pi}(s).
V_0 \rightarrow V_1 \rightarrow V_2 \rightarrow \ldots \rightarrow V_k \rightarrow V_{k+1} \rightarrow \ldots \rightarrow V^\pi
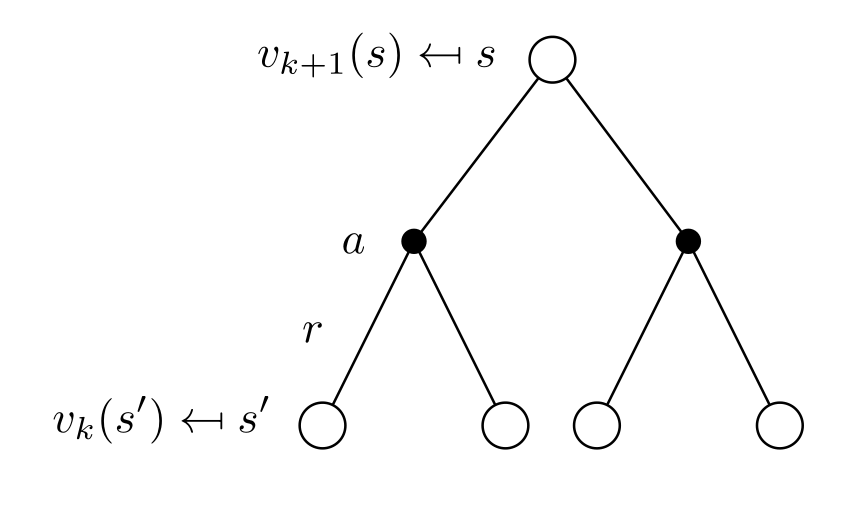
The value function at step k+1 V_{k+1}(s) is computed using the previous estimates V_{k}(s) and the Bellman equation transformed into an update rule.
\mathbf{V}_{k+1} = \mathbf{R}^\pi + \gamma \, \mathcal{P}^\pi \, \mathbf{V}_k
V_\infty = V^{\pi} is a fixed point of this update rule because of the uniqueness of the solution to the Bellman equation.
For each state s, we would like to know if we should deterministically choose an action a \neq \pi(s) or not in order to improve the policy. The value of an action a in the state s for the policy \pi is given by:
Q^{\pi} (s, a) = \sum_{s' \in \mathcal{S}} p(s' | s, a) \, [r(s, a, s') + \gamma \, V^{\pi}(s') ]
If the Q-value of an action a is higher than the one currently selected by the deterministic policy:
Q^{\pi} (s, a) > Q^{\pi} (s, \pi(s)) = V^{\pi}(s)
then it is better to select a once in s and thereafter follow \pi. If there is no better action, we keep the previous policy for this state. This corresponds to a greedy action selection over the Q-values, defining a deterministic policy \pi(s):
\pi(s) \leftarrow \text{argmax}_a \, Q^{\pi} (s, a) = \sum_{s' \in \mathcal{S}} p(s' | s, a) \, [r(s, a, s') + \gamma \, V^{\pi}(s') ]
After the policy improvement, the Q-value of each deterministic action \pi(s) has increased or stayed the same.
\text{argmax}_a \; Q^{\pi} (s, a) = \sum_{s' \in \mathcal{S}} p(s' | s, a) \, [r(s, a, s') + \gamma \, V^{\pi}(s') ] \geq Q^\pi(s, \pi(s))
This defines an improved policy \pi', where all states and actions have a higher value than previously. Greedy action selection over the state value function implements policy improvement:
\pi' \leftarrow \text{Greedy}(V^\pi)
Once a policy \pi has been improved using V^{\pi} to yield a better policy \pi', we can then compute V^{\pi'} and improve it again to yield an even better policy \pi''. The algorithm policy iteration successively uses policy evaluation and policy improvement to find the optimal policy.
\pi_0 \xrightarrow[]{E} V^{\pi_0} \xrightarrow[]{I} \pi_1 \xrightarrow[]{E} V^{\pi^1} \xrightarrow[]{I} ... \xrightarrow[]{I} \pi^* \xrightarrow[]{E} V^{*}
The optimal policy being deterministic, policy improvement can be greedy over the state-action values. If the policy does not change after policy improvement, the optimal policy has been found.
Value iteration
One drawback of policy iteration is that it uses a full policy evaluation, which can be computationally exhaustive as the convergence of V_k is only at the limit and the number of states can be huge. The idea of value iteration is to interleave policy evaluation and policy improvement, so that the policy is improved after EACH iteration of policy evaluation, not after complete convergence.
As policy improvement returns a deterministic greedy policy, updating of the value of a state is then simpler:
V_{k+1}(s) = \max_a \sum_{s'} p(s' | s,a) [r(s, a, s') + \gamma \, V_k(s') ]
Note that this is equivalent to turning the Bellman optimality equation into an update rule. Value iteration converges to V^*, faster than policy iteration, and should be stopped when the values do not change much anymore.
Summary
Policy-iteration and value-iteration consist of alternations between policy evaluation and policy improvement, and converge to the optimal policy. This principle is called Generalized Policy Iteration (GPI). Solving the Bellman equations requires the following:
- accurate knowledge of environment dynamics p(s' | s, a) and r(s, a, s') for all transitions;
- enough memory and time to do the computations;
- the Markov property.
Finding an optimal policy is polynomial in the number of states and actions: \mathcal{O}(N^2 \, M) (N is the number of states, M the number of actions). The number of states is often astronomical (e.g., Go has about 10^{170} states), often growing exponentially with the number of state variables (what Bellman called “the curse of dimensionality”). In practice, classical DP can only be applied to problems with a few millions of states.