Advantage Actor-Critic (A3C)

Actor-critic algorithms

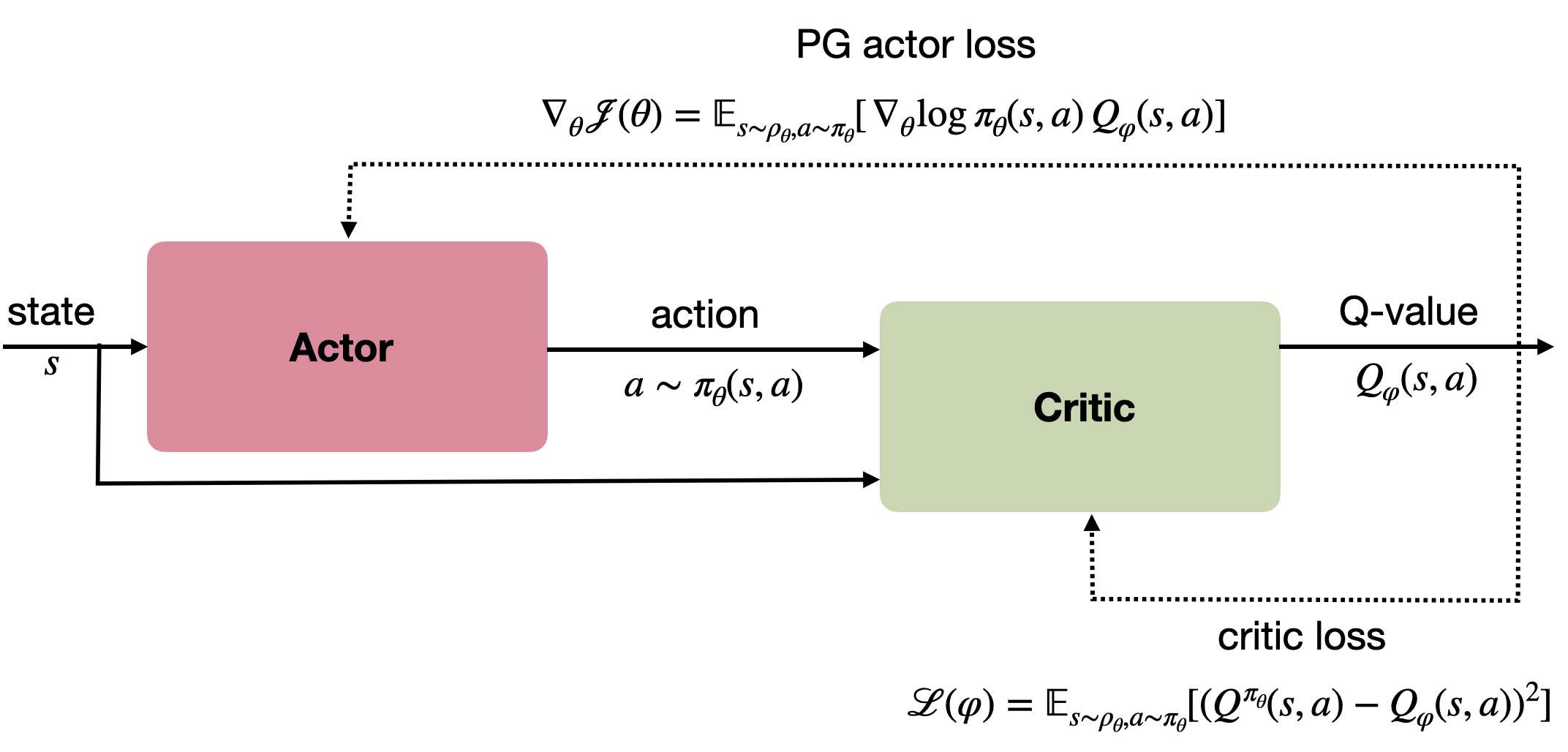
The policy gradient theorem provides an actor-critic arhictecture that allow to estimate the PG from single transitions:

\nabla_\theta J(\theta) = \mathbb{E}_{s \sim \rho_\theta, a \sim \pi_\theta}[\nabla_\theta \log \pi_\theta(s, a) \, Q_\varphi(s, a))]

Figure 1: Architecture of the policy gradient (PG) method.

The critic can be trained with any advantage estimator, including Q-learning. It is common to use the DQN loss (or any variant of it: double DQN, n-step, etc) for the critic.

\mathcal{L}(\varphi) = \mathbb{E}_{s_t \sim \rho_\theta, a_t \sim \pi_\theta} [(r(s, a, s') + \gamma \, Q_{\varphi'}(s', \text{argmax}_{a'} Q_\varphi (s', a')) - Q_\varphi (s, a) )^2]

Most policy-gradient algorithms in this section are actor-critic architectures. The different versions of the policy gradient take the form:

\nabla_\theta J(\theta) = \mathbb{E}_{s_t \sim \rho^\pi, a_t \sim \pi_\theta}[\nabla_\theta \log \pi_\theta (s_t, a_t) \, \psi_t ]

where:

• \psi_t = R_t is the REINFORCE algorithm (MC sampling).

• \psi_t = R_t - b is the REINFORCE with baseline algorithm.

• \psi_t = Q^\pi(s_t, a_t) is the policy gradient theorem.

• \psi_t = A^\pi(s_t, a_t) is the advantage actor-critic.

• \psi_t = r_{t+1} + \gamma \, V^\pi(s_{t+1}) - V^\pi(s_t) is the TD actor-critic.

• \psi_t = \sum_{k=0}^{n-1} \gamma^{k} \, r_{t+k+1} + \gamma^n \, V^\pi(s_{t+n+1}) - V^\pi(s_t) is the n-step advanatge actor-critic (A2C).

Generally speaking:

• the more \psi_t relies on real rewards (e.g. R_t), the more the gradient will be correct on average (small bias), but the more it will vary (high variance). This increases the sample complexity: we need to average more samples to correctly estimate the gradient.
• the more \psi_t relies on estimations (e.g. the TD error), the more stable the gradient (small variance), but the more incorrect it is (high bias). This can lead to suboptimal policies, i.e. local optima of the objective function.

This is the classical bias/variance trade-off in machine learning. n-step advantages are an attempt to mitigate between these extrema. Schulman et al. (2015) proposed the Generalized Advantage Estimate (GAE, see Section Generalized Advantage Estimation (GAE)) to further control the bias/variance trade-off.

Note: A2C is actually derived from the A3C algorithm presented later, but it is simpler to explain it first. See https://openai.com/index/openai-baselines-acktr-a2c/ for an explanation of the reasons. A good explanation of A2C and A3C with Python code is available at https://cgnicholls.github.io/reinforcement-learning/2017/03/27/a3c.html.

Advantage Actor-Critic (A2C)

The first aspect of A2C is that it relies on n-step updating, which is a trade-off between MC and TD:

• MC waits until the end of an episode to update the value of an action using the reward to-go (sum of obtained rewards) R(s, a).
• TD updates immediately the action using the immediate reward r(s, a, s') and approximates the rest with the value of the next state V^\pi(s).
• n-step uses the n next immediate rewards and approximates the rest with the value of the state visited n steps later.

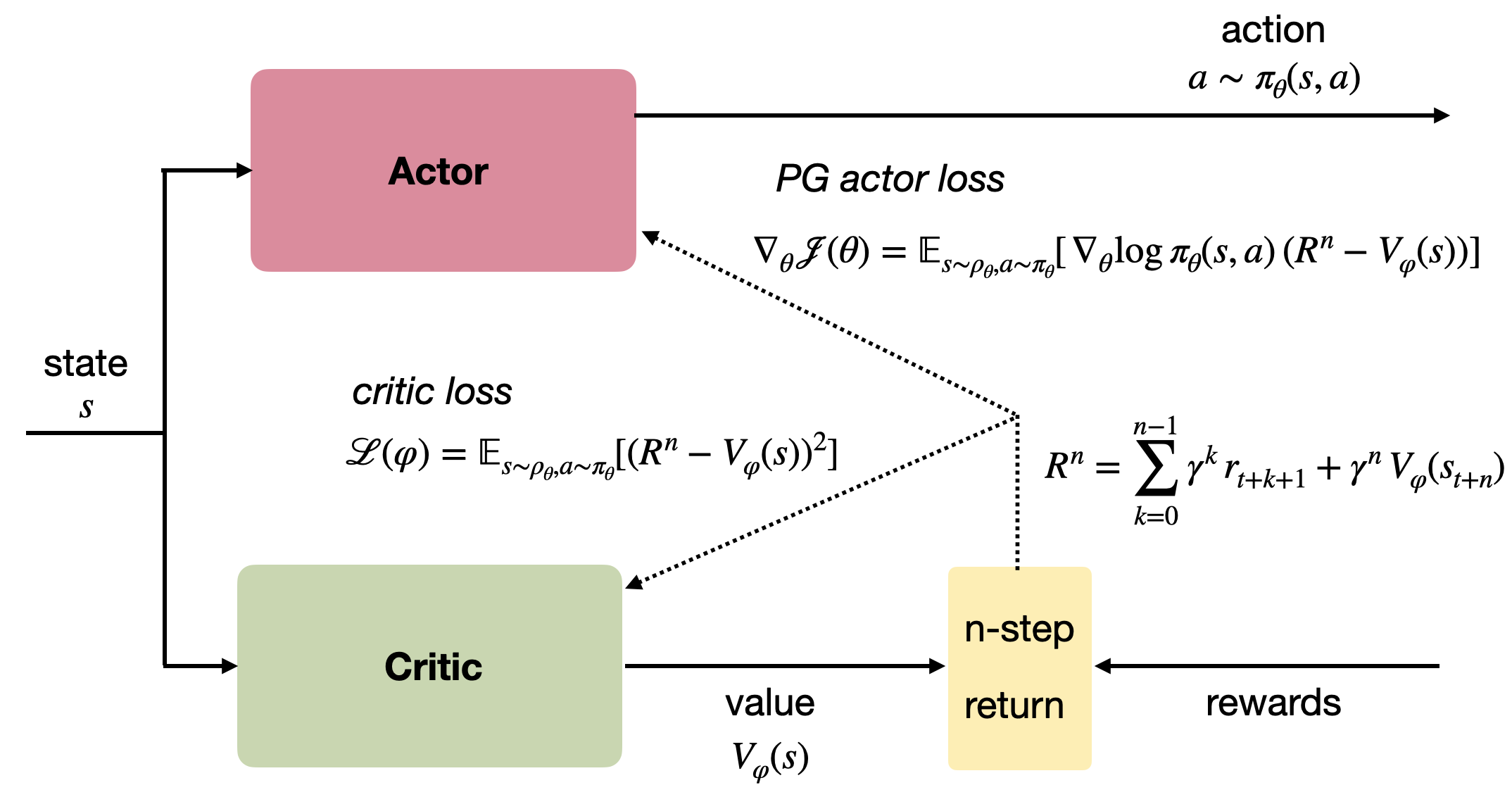
\nabla_\theta J(\theta) = \mathbb{E}_{s_t \sim \rho^\pi, a_t \sim \pi_\theta}[\nabla_\theta \log \pi_\theta(s_t, a_t) \, ( \sum_{k=0}^{n-1} \gamma^{k} \, r_{t+k+1} + \gamma^n \, V_\varphi(s_{t+n+1}) - V_\varphi(s_t))]

A2C has an actor-critic architecture:

• The actor outputs the policy \pi_\theta for a state s, i.e. a vector of probabilities for each action.
• The critic outputs the value V_\varphi(s) of a state s.

Figure 2: Advantage actor-critic architecture.

Having a computable formula for the policy gradient, the algorithm is rather simple:

1. Acquire a batch of transitions (s, a, r, s') using the current policy \pi_\theta (either a finite episode or a truncated one).

2. For each state encountered, compute the discounted sum of the next n rewards \sum_{k=0}^{n} \gamma^{k} \, r_{t+k+1} and use the critic to estimate the value of the state encountered n steps later V_\varphi(s_{t+n+1}).

R_t = \sum_{k=0}^{n-1} \gamma^{k} \, r_{t+k+1} + \gamma^n \, V_\varphi(s_{t+n+1})

3. Update the actor.

\nabla_\theta J(\theta) = \sum_t \nabla_\theta \log \pi_\theta(s_t, a_t) \, (R_t - V_\varphi(s_t))

4. Update the critic to minimize the TD error between the estimated value of a state and its true value.

\mathcal{L}(\varphi) = \sum_t (R_t - V_\varphi(s_t))^2

5. Repeat.

This is not very different in essence from REINFORCE (sample transitions, compute the return, update the policy), apart from the facts that episodes do not need to be finite and that a critic has to be learned in parallel. A more detailed pseudo-algorithm for a single A2C learner is the following:

A2C algorithm for a single worker/learner

• Initialize the actor \pi_\theta and the critic V_\varphi with random weights.

• Observe the initial state s_0.

• while not converged:

  • Initialize empty episode minibatch.

  • for k \in [0, n]: # Sample episode

    • Select a action a_k using the actor \pi_\theta.

    • Perform the action a_k and observe the next state s_{k+1} and the reward r_{k+1}.

    • Store (s_k, a_k, r_{k+1}) in the episode minibatch.

  • if s_n is not terminal: set R = V_\varphi(s_n) with the critic, else R=0.

  • Reset gradient d\theta and d\varphi to 0.

  • for k \in [n-1, 0]: # Backwards iteration over the episode

    • Update the discounted sum of rewards R = r_k + \gamma \, R

    • Accumulate the policy gradient using the critic:

    d\theta \leftarrow d\theta + \nabla_\theta \log \pi_\theta(s_k, a_k) \, (R - V_\varphi(s_k))

    • Accumulate the critic gradient:

    d\varphi \leftarrow d\varphi + \nabla_\varphi (R - V_\varphi(s_k))^2

  • Update the actor and the critic with the accumulated gradients using gradient descent or similar:

  \theta \leftarrow \theta + \eta \, d\theta \qquad \varphi \leftarrow \varphi + \eta \, d\varphi

Note that not all states are updated with the same horizon n: the last action encountered in the sampled episode will only use the last reward and the value of the final state (TD learning), while the very first action will use the n accumulated rewards. In practice it does not really matter, but the choice of the discount rate \gamma will have a significant influence on the results.

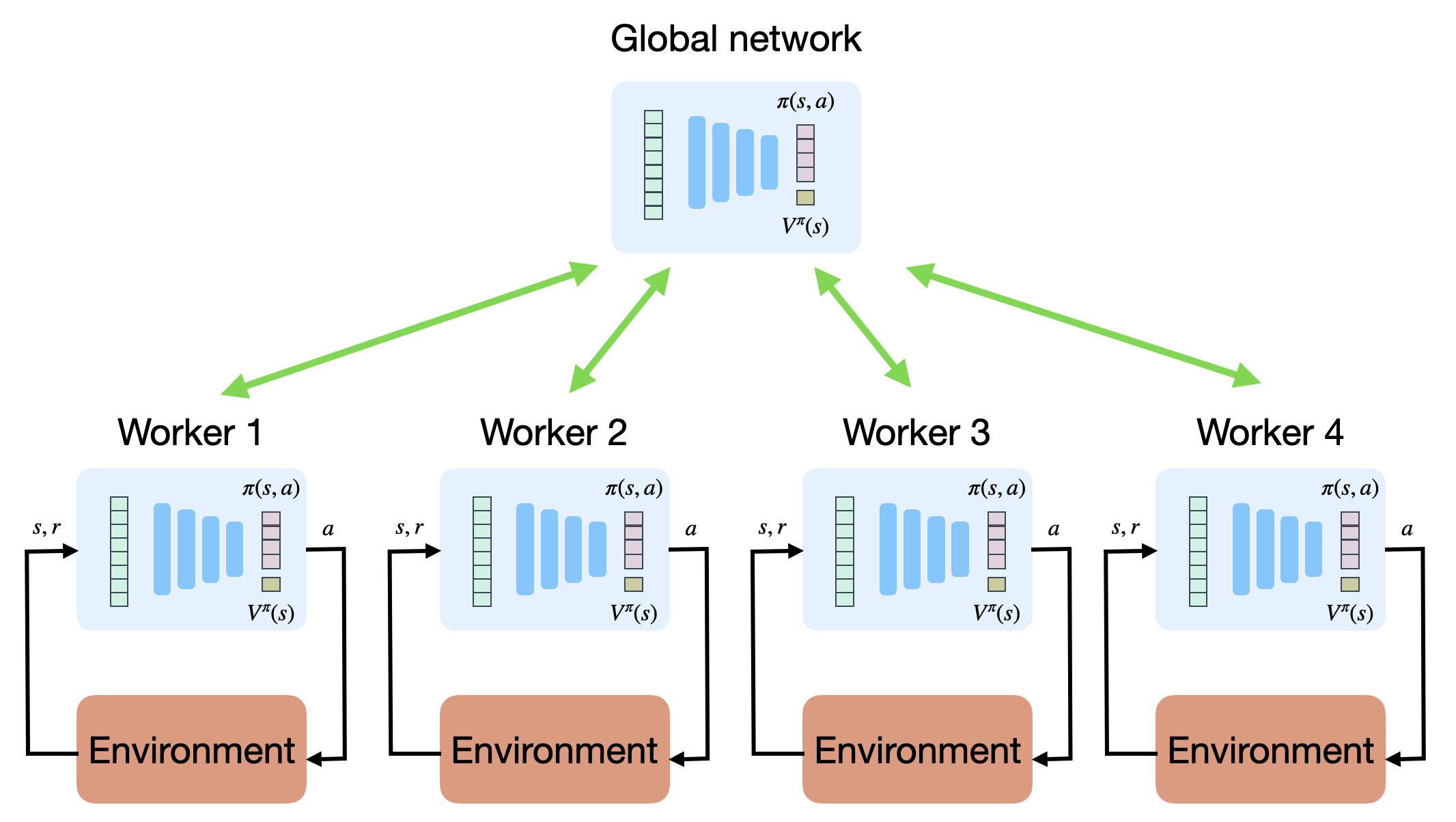
As many actor-critic methods, A2C performs online learning: a couple of transitions are explored using the current policy, which is immediately updated. As for value-based networks (e.g. DQN), the underlying NN will be affected by the correlated inputs and outputs: a single batch contains similar states and action (e.g. consecutive frames of a video game). The solution retained in A2C and A3C does not depend on an experience replay memory as DQN, but rather on the use of multiple parallel actors and learners (see Section Distributed learning).

The idea is depicted on Figure 3 (actually for A3C, but works with A2C). The actor and critic are stored in a global network. Multiple instances of the environment are created in different parallel threads (the workers). At the beginning of an episode, each worker receives a copy of the actor and critic weights from the global network. Each worker samples an episode (starting from different initial states, so the episodes are uncorrelated), computes the accumulated gradients and sends them back to the global network. The global networks merges the gradients and uses them to update the parameters of the policy and critic networks. The new parameters are send to each worker again, until it converges.

Distributed A2C algorithm

• Initialize the actor \pi_\theta and the critic V_\varphi in the global network.

• while not converged:

  • for each worker i in parallel:

    • Get a copy of the global actor \pi_\theta and critic V_\varphi.

    • Sample an episode of n steps.

    • Return the accumulated gradients d\theta_i and d\varphi_i.

  • Wait for all workers to terminate.

  • Merge all accumulated gradients into d\theta and d\varphi.

  • Update the global actor and critic networks.

This solves the problem of correlated inputs and outputs, as each worker explores different regions of the environment (one can set different initial states in each worker, vary the exploration rate, etc), so the final batch of transitions used for training the global networks is much less correlated. The only drawback of this approach is that it has to be possible to explore multiple environments in parallel. This is easy to achieve in simulated environments (e.g. video games) but much harder in real-world systems like robots. A brute-force solution for robotics is simply to buy enough robots and let them learn in parallel (Gu et al., 2017).

Asynchronous Advantage Actor-Critic (A3C)

Figure 3: Distributed architecture of A3C. A global network interacts asynchronously with several workers, each having a copy of the network and interacting with a separate environment. At the end of an episode, the accumulated gradients are sent back to the master network, and a new value of the parameters is sent to the workers.

Asynchronous Advantage Actor-Critic (A3C, Mnih et al., 2016) extends the approach of A2C by removing the need of synchronization between the workers at the end of each episode before applying the gradients. The rationale behind this is that each worker may need different times to complete its task, so they need to be synchronized. Some workers might then be idle most of the time, what is a waste of resources. Gradient merging and parameter updates are sequential operations, so no significant speedup is to be expected even if one increases the number of workers.

The solution retained in A3C is to simply skip the synchronization step: each worker reads and writes the network parameters whenever it wants. Without synchronization barriers, there is of course a risk that one worker tries to read the network parameters while another writes them: the obtained parameters would be a mix of two different networks. Surprisingly, it does not matter: if the learning rate is small enough, there is anyway not a big difference between two successive versions of the network parameters. This kind of “dirty” parameter sharing is called HogWild! updating (Niu et al., 2011) and has been proven to work under certain conditions which are met here.

The resulting A3C pseudocode is summarized here:

Distributed A3C algorithm

• Initialize the actor \pi_\theta and the critic V_\varphi in the global network.

• for each worker i in parallel:

  • repeat:

    • Get a copy of the global actor \pi_\theta and critic V_\varphi.

    • Sample an episode of n steps.

    • Compute the accumulated gradients d\theta_i and d\varphi_i.

    • Update the global actor and critic networks asynchronously (HogWild!).

The workers are fully independent: their only communication is through the asynchronous updating of the global networks. This can lead to very efficient parallel implementations: in the original A3C paper (Mnih et al., 2016), they solved the same Atari games than DQN using 16 CPU cores instead of a powerful GPU, while achieving a better performance in less training time (1 day instead of 8). The speedup is almost linear: the more workers, the faster the computations, the better the performance (as the policy updates are less correlated).

Entropy regularization

An interesting addition in A3C is the way they enforce exploration during learning. In actor-critic methods, exploration classically relies on the fact that the learned policies are stochastic (on-policy): \pi(s, a) describes the probability of taking the action a in the state s. In discrete action spaces, the output of the actor can be a softmax layer, ensuring that all actions get a non-zero probability of being selected during training. In continuous action spaces, the executed action is sampled from the output probability distribution. However, this is often not sufficient and hard to control.

In A3C, the authors added an entropy regularization term (Williams and Peng, 1991) to the policy gradient update:

\nabla_\theta J(\theta) = \mathbb{E}_{s_t \sim \rho^\pi, a_t \sim \pi_\theta}[\nabla_\theta \log \pi_\theta(s_t, a_t) \, ( R_t - V_\varphi(s_t)) + \beta \, \nabla_\theta H(\pi_\theta(s_t))]

For discrete actions, the entropy of the policy for a state s_t is simple to compute:

H(\pi_\theta(s_t)) = - \sum_a \pi_\theta(s_t, a) \, \log \pi_\theta(s_t, a)

It measures the “randomness” of the policy: if the policy is fully deterministic (the same action is systematically selected), the entropy is zero as it carries no information. If the policy is completely random, the entropy is maximal. Maximizing the entropy at the same time as the returns improves exploration by forcing the policy to be as non-deterministic as possible.

See Section Maximum Entropy RL (SAC) for more details on using the entropy for exploration.

Actor-critic neural architectures

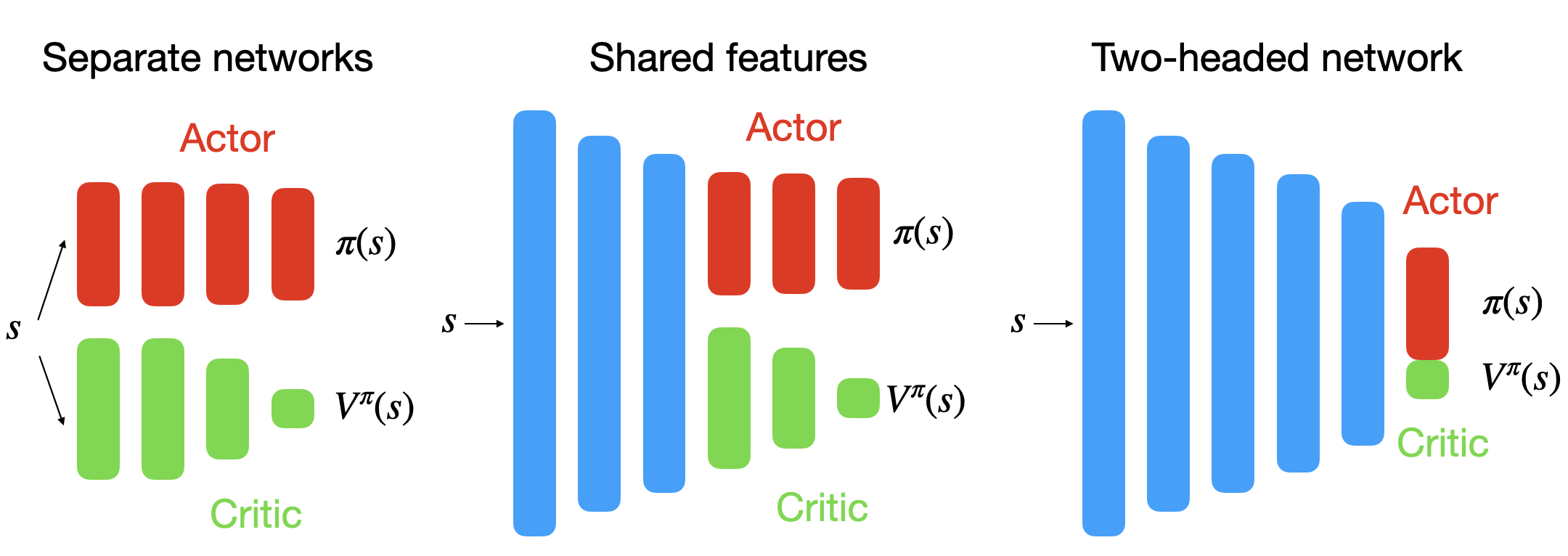
We have considered that actor-critic architectures consist of two separate neural networks, the actor \pi(s, a) and the critic Q(s, a) both taking the state s (or observation o) as an input and outputing one value per action. Each of these networks have their own loss function. They share nothing except the “data”. Is it really the best option?

When working on images, the first few layers of the CNNs are likely to learn the same visual features (edges, contours). It would be more efficient to share some of the extracted features. Actor-critic architectures can share layers between the actor and the critic, sometimes up to the output layer. A compound loss sums the losses for the actor and the critic. Tensorflow/pytorch know which parameters influence which part of the loss.

\mathcal{L}(\theta) = \mathcal{L}_\text{actor}(\theta) + \mathcal{L}_\text{critic}(\theta)

For pixel-based environments (Atari), the networks often share the convolutional layers. For continuous environments (Mujoco), separate networks sometimes work better than two-headed networks.

Figure 4: The actor and the critic can share no/some/most layers, depending on the algorithm and the application.

Continuous action spaces

The actor-critic methods presented above use stochastic policies \pi_\theta(s, a) assigning parameterized probabilities of being selecting to each (s, a) pair.

• When the action space is discrete, the output layer of the actor is simply a softmax layer with as many neurons as possible actions in each state, making sure the probabilities sum to one. It is then straightforward to sample an action from this layer.

• When the action space is continuous, one has to make an assumption on the underlying distribution. The actor learns the parameters of the distribution and the executed action is simply sampled from the parameterized distribution.

Suppose that we want to control a robotic arm with n degrees of freedom. An action \mathbf{a} could be a vector of joint displacements:

\mathbf{a} = \begin{bmatrix} \Delta \theta_1 & \Delta \theta_2 & \ldots \, \Delta \theta_n\end{bmatrix}^T

The output layer of the policy network can very well represent this vector, but how would we implement exploration? \epsilon-greedy and softmax action selection would not work, as all output neurons are useful.

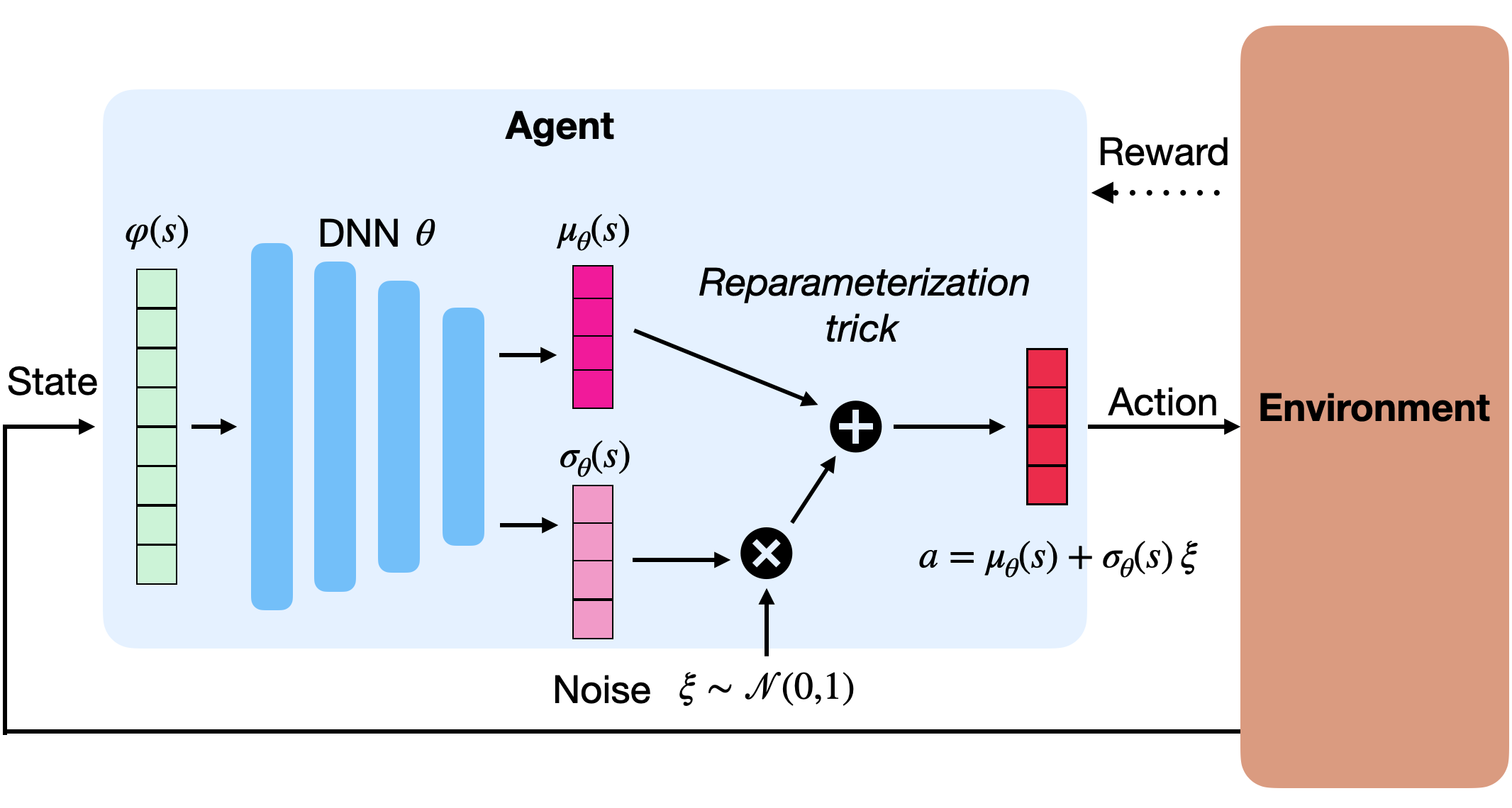
The most common solution is to use a stochastic Gaussian policy, based on the Gaussian distribution. In this case, the output of the actor is a mean vector \mu_\theta(s) and a variance vector \sigma_\theta(s), providing the parameters of the normal distribution. The policy \pi_\theta(s, a) = \mathcal{N}(\mu_\theta(s), \sigma^2_\theta(s)) is then simply defined as:

\pi_\theta(s, a) = \frac{1}{\sqrt{2\pi\sigma^2_\theta(s)}} \, \exp -\frac{(a - \mu_\theta(s))^2}{2\sigma_\theta(s)^2}

Figure 5: Reparameterization trick to implement continuous stochastic Gaussian policies.

In order to use backpropagation on the policy gradient (i.e. getting an analytical form of the score function \nabla_\theta \log \pi_\theta (s, a)), one can use the reparameterization trick (Heess et al., 2015) by rewriting the policy as:

a = \mu_\theta(s) + \sigma_\theta(s) \times \xi \qquad \text{where} \qquad \xi \sim \mathcal{N}(0,1)

To select an action, we only need to sample \xi from the unit normal distribution, multiply it by the standard deviation and add the mean. To compute the score function, we use the following partial derivatives:

\nabla_\mu \log \pi_\theta (s, a) = \frac{a - \mu_\theta(s)}{\sigma_\theta(s)^2} \qquad \nabla_\sigma \log \pi_\theta (s, a) = \frac{(a - \mu_\theta(s))^2}{\sigma_\theta(s)^3} - \frac{1}{\sigma_\theta(s)}

and use the chain rule to obtain the score function. The reparameterization trick is a cool trick to apply backpropagation on stochastic problems: it is for example used in the variational auto-encoders [VAE; Kingma and Welling (2013)].

Depending on the problem, one could use: 1) a fixed \sigma for the whole action space, 2) a fixed \sigma per DoF, 3) a learnable \sigma per DoF (assuming all action dimensions to be mutually independent) or even 4) a covariance matrix \Sigma when the action dimensions are dependent.

One limitation of Gaussian policies is that their support is infinite: even with a small variance, samples actions can deviate a lot (albeit rarely) from the mean. This is particularly a problem when action must have a limited range: the torque of an effector, the linear or angular speed of a car, etc. Clipping the sampled action to minimal and maximal values introduces a bias which can impair learning. Chou et al. (2017) proposed to use beta-distributions instead of Gaussian ones in the actor. Sampled values have a [0,1] support, which can rescaled to [v_\text{min},v_\text{max}] easily. They show that beta policies have less bias than Gaussian policies in most continuous problems.

Chou, P.-W., Maturana, D., and Scherer, S. (2017). Improving Stochastic Policy Gradients in Continuous Control with Deep Reinforcement Learning using the Beta Distribution. in International Conference on Machine Learning Available at: http://proceedings.mlr.press/v70/chou17a/chou17a.pdf.

Gu, S., Holly, E., Lillicrap, T., and Levine, S. (2017). Deep Reinforcement Learning for Robotic Manipulation with Asynchronous Off-Policy Updates. in Proc. ICRA Available at: http://arxiv.org/abs/1610.00633.

Heess, N., Wayne, G., Silver, D., Lillicrap, T., Tassa, Y., and Erez, T. (2015). Learning continuous control policies by stochastic value gradients. Proc. International Conference on Neural Information Processing Systems, 2944–2952. Available at: http://dl.acm.org/citation.cfm?id=2969569.

Kingma, D. P., and Welling, M. (2013). Auto-Encoding Variational Bayes. Available at: http://arxiv.org/abs/1312.6114.

Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T. P., Harley, T., et al. (2016). Asynchronous Methods for Deep Reinforcement Learning. in Proc. ICML Available at: http://arxiv.org/abs/1602.01783.

Niu, F., Recht, B., Re, C., and Wright, S. J. (2011). HOGWILD!: A Lock-Free Approach to Parallelizing Stochastic Gradient Descent. in Proc. Advances in Neural Information Processing Systems, 21–21. Available at: http://arxiv.org/abs/1106.5730.

Schulman, J., Levine, S., Abbeel, P., Jordan, M., and Moritz, P. (2015). Trust Region Policy Optimization. in Proceedings of the 31 st International Conference on Machine Learning, 1889–1897. Available at: http://proceedings.mlr.press/v37/schulman15.html.

Williams, R. J., and Peng, J. (1991). Function optimization using connectionist reinforcement learning algorithms. Connection Science 3, 241–268.