Model-based-augmented model-free RL (Dyna-Q, I2A)
Dyna-Q
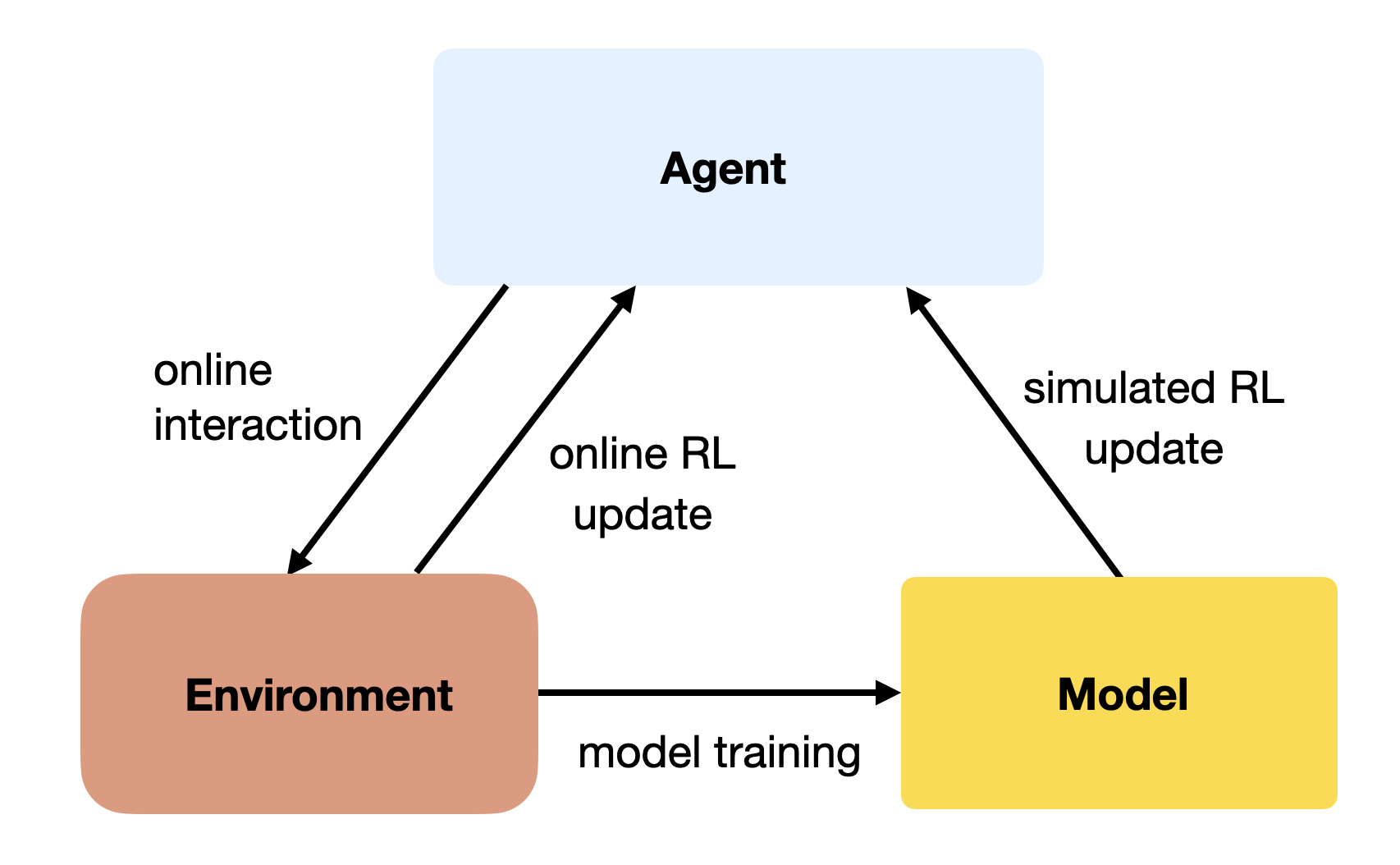
Once a model of the environment is learned, it is possible to augment MF algorithms with MB transitions. The MF algorithm (e.g. Q-learning) learns from transitions (s, a, r, s') sampled either with:
- real experience: online interaction with the environment.
- simulated experience: simulated transitions by the model.
If the simulated transitions are realistic enough, the MF algorithm can converge using much less real transitions, thereby reducing its sample complexity.
The Dyna-Q algorithm (Sutton, 1990) is an extension of Q-learning to integrate a model M(s, a) = (s', r'). It alternates between online updates of the agent using the real environment and (possible multiple) offline updates using the model.
It is interesting to notice that Dyna-Q is the inspiration for DQN and its experience replay memory. In DQN, the ERM stores real transitions generated in the past and recovers them later intact, while in Dyna-Q, the model generates imagined transitions approximated based on past real transitions. Interleaving on-policy and off-policy updates is also the core idea of ACER (section Actor-Critic with Experience Replay (ACER)).
I2A - Imagination-augmented agents
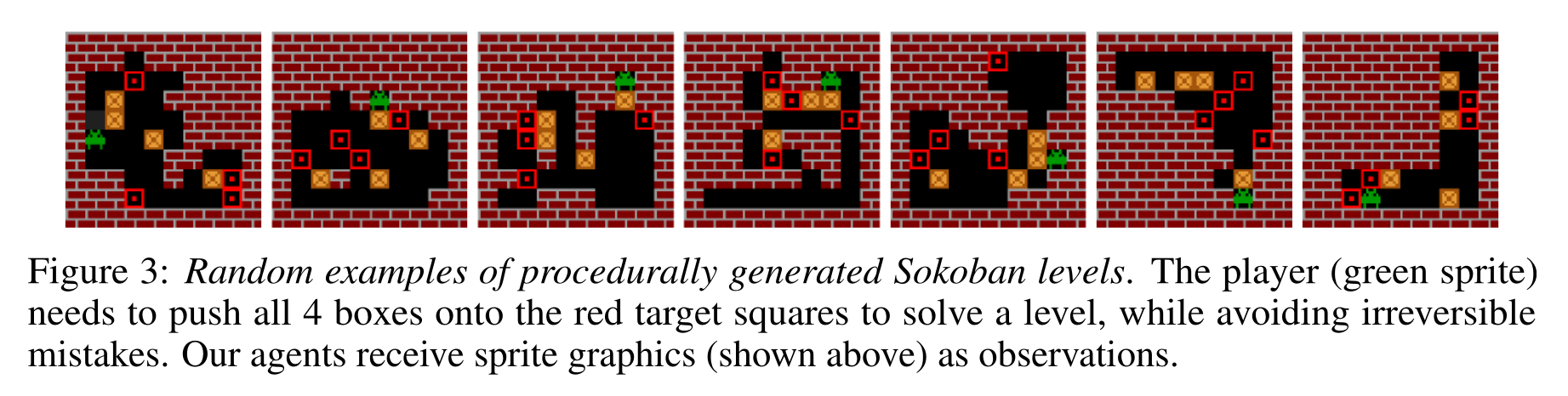
I2A (Weber et al., 2017) is a model-based augmented model-free method: it trains a MF algorithm (A3C) with the help of rollouts generated by a MB model. The authors showcase their algorithm on the puzzle environment Sokoban, where you need to move boxes to specified locations.
Sokoban is a quite hard game, as actions are irreversible (you can get stuck) and the solution requires many actions (sparse rewards). MF methods are bad at this game as they learn through trials-and-(many)-errors.
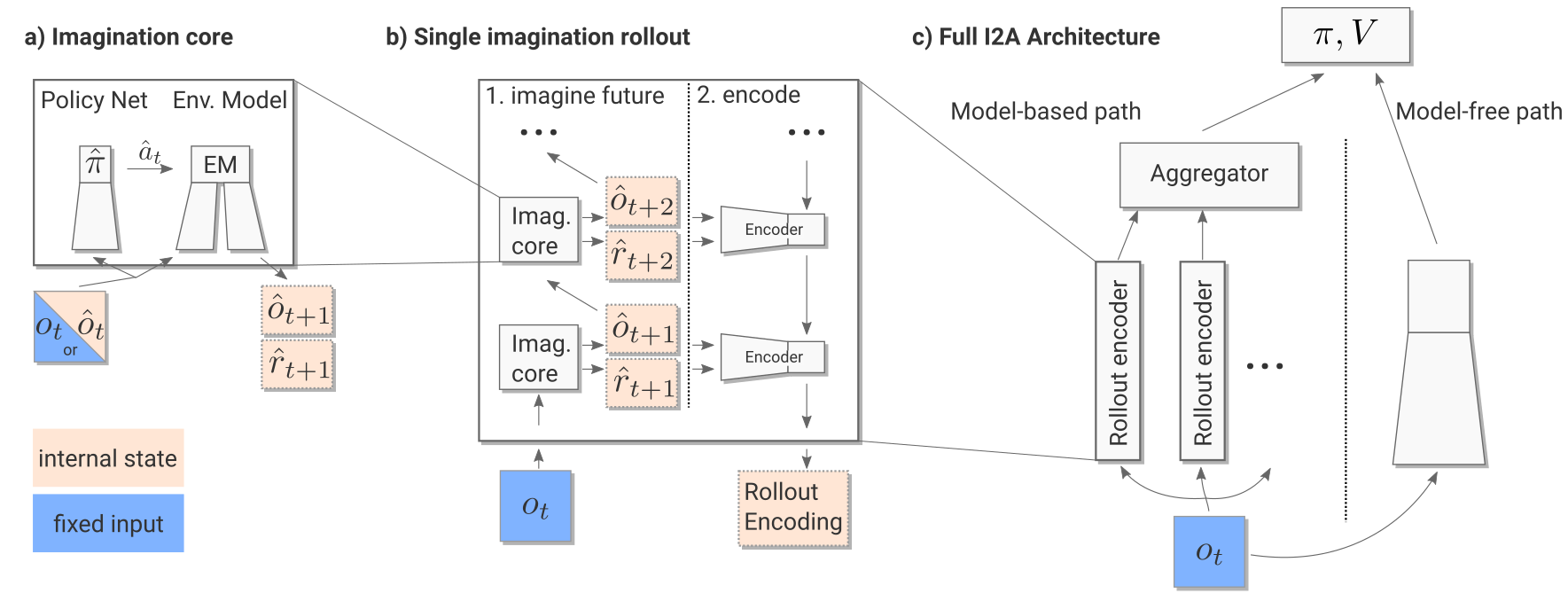
I2A is composed of several different modules. We will now have a look at them one by one.
Environment model
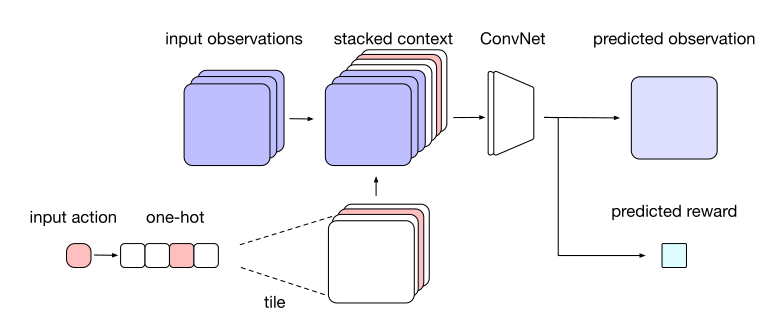
The environment model learns to predict the next frame and the next reward based on the four last frames and the chosen action:
(o_{t-3}, o_{t-2}, o_{t-1}, o_{t}, a_t) \rightarrow (o_{t+1}, r_{t+1})
As Sokoban is a POMDP (partially observable), the notation uses observations o_t instead of states s_t, but it does not really matter here.
The neural network is a sort of convolutional autoencoder, taking additionally an action a as input and predicting the next reward. Formally, the output “image” being different from the input, the neural network is not an autoencoder but belongs to the family of segmentation networks such as SegNet (Badrinarayanan et al., 2016) or U-net (Ronneberger et al., 2015). It can be pretrained using a random policy, and later fine-tuned during training.
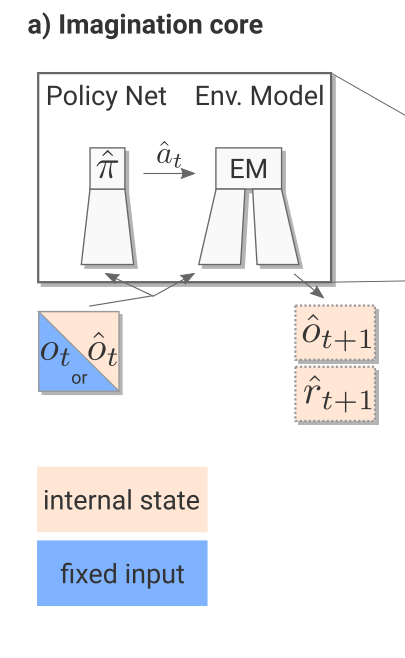
Imagination core
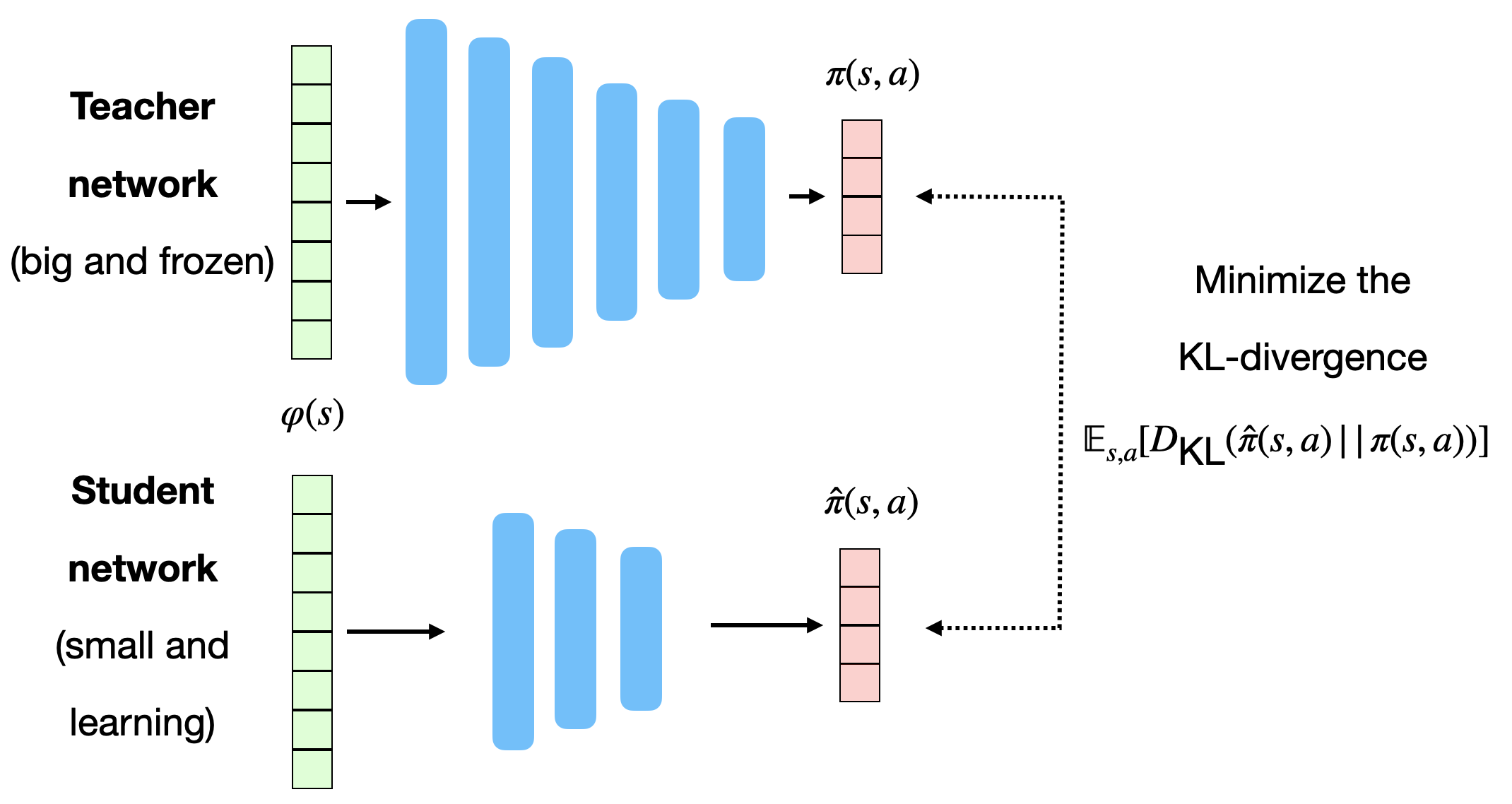
The imagination core is composed of the environment model M(s, a) and a rollout policy \hat{\pi}. The rollout policy \hat{\pi} is a simple and fast policy. It does not have to be the trained policy \pi: It could even be a random policy, or a pretrained policy using for example A3C directly. In I2A, the rollout policy \hat{\pi} is obtained through policy distillation of the bigger policy network \pi.
The small rollout policy network \hat{\pi} tries to copy the outputs \pi(s, a) of the whole model. This is a supervised learning task: we just need minimize the KL divergence between the two policies:
\mathcal{L}(\hat{\theta}) = \mathbb{E}_{s, a} [D_\text{KL}(\hat{\pi}(s, a) || \pi(s, a))]
As the network is smaller, it won’t be quite as good as \pi (although not dramatically), but its learning objective is simpler: supervised learning is much easier than RL, especially when the rewards are sparse. A very small network (up to 90% of the original parameters) is often enough for the same functionality.
In general, policy distillation can be used to ensure generalization over different environments, as in Distral (Teh et al., 2017). Each learning algorithms learns its own task, but tries not to diverge too much from a shared policy, which turns out to be good at all tasks.
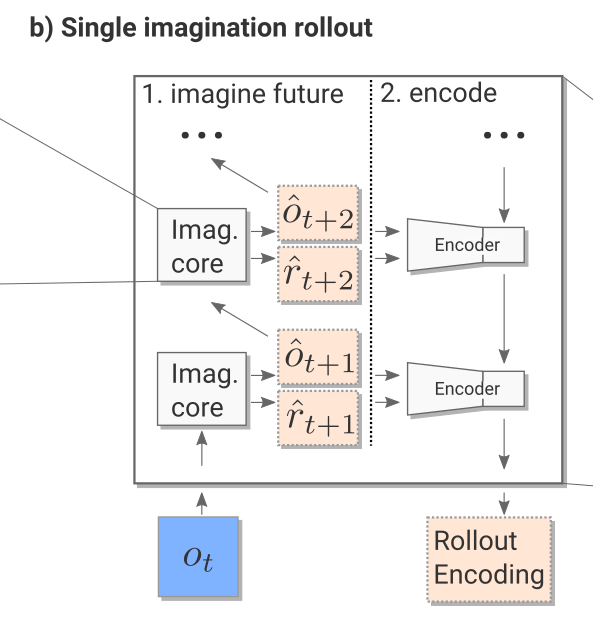
Imagination rollout module
The imagination rollout module uses the imagination core to predict iteratively the next \tau frames and rewards using the current frame o_t and the rollout policy:
(o_{t-3}, o_{t-2}, o_{t-1}, o_{t}) \rightarrow \hat{o}_{t+1} \rightarrow \hat{o}_{t+2} \rightarrow \ldots \rightarrow \hat{o}_{t+\tau}
The \tau frames and rewards are passed backwards to a convolutional LSTM (from t+\tau to t) which produces an embedding / encoding of the rollout. The output of the imagination rollout module is a vector e_i (the final state of the LSTM) representing the whole rollout, including the (virtually) obtained rewards. Note that because of the stochasticity of the rollout policy \hat{\pi}, different rollouts can lead to different encoding vectors.
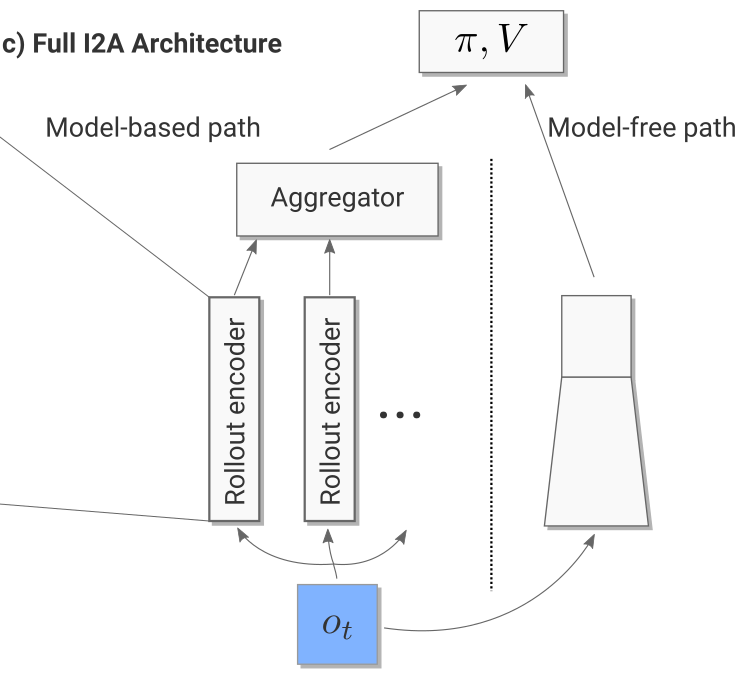
Model-free path
For the current observation o_t (and the three frames before), we then generate one rollout per possible action (5 in Sokoban):
- What would happen if I do action 1?
- What would happen if I do action 2?
- etc.
The resulting vectors are concatenated to the output of model-free path (a convolutional neural network taking the current observation as input).
Full model
Altogether, we have a huge NN with weights \theta (model, rollout encoder, MF path) between the input observation o_t and the output policy \pi (plus the critic V).
We can then learn the policy \pi and value function V using the n-step advantage actor-critic (A3C) :
\nabla_\theta \mathcal{J}(\theta) = \mathbb{E}_{s_t \sim \rho_\theta, a_t \sim \pi_\theta}[\nabla_\theta \log \pi_\theta (s_t, a_t) \, (\sum_{k=0}^{n-1} \gamma^{k} \, r_{t+k+1} + \gamma^n \, V_\varphi(s_{t+n}) - V_\varphi(s_t)) ]
\mathcal{L}(\varphi) = \mathbb{E}_{s_t \sim \rho_\theta, a_t \sim \pi_\theta}[(\sum_{k=0}^{n-1} \gamma^{k} \, r_{t+k+1} + \gamma^n \, V_\varphi(s_{t+n}) - V_\varphi(s_t))^2]
The complete architecture may seem complex, but everything is differentiable so we can apply backpropagation and train the network end-to-end using multiple workers. It is simply the A3C algorithm (MF), but augmented by MB rollouts, i.e. with explicit information about the (emulated) future.
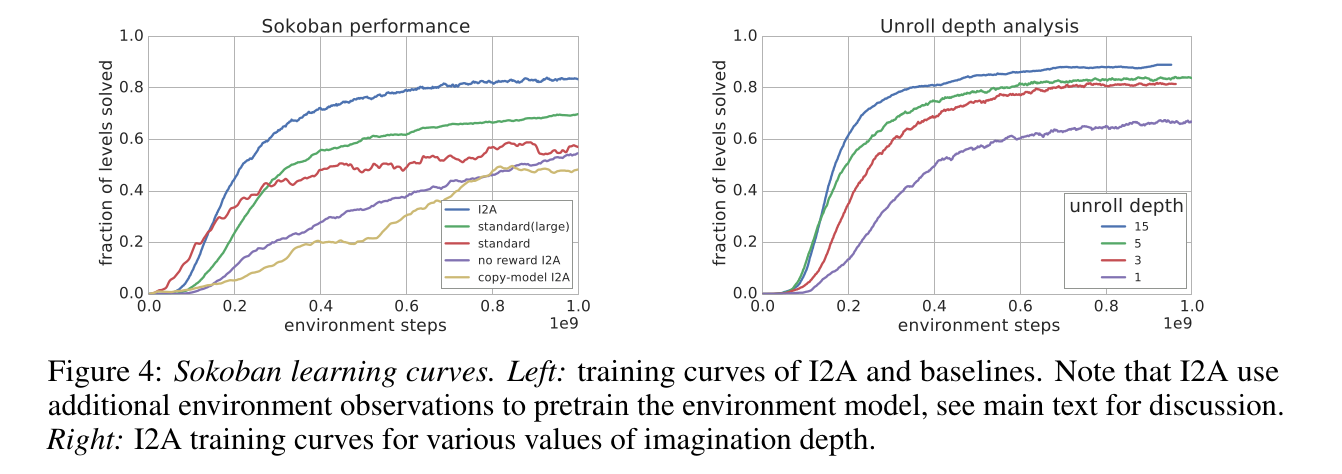
Results
Unsurprisingly, I2A performs better than A3C on Sokoban. The deeper the rollout, the better:
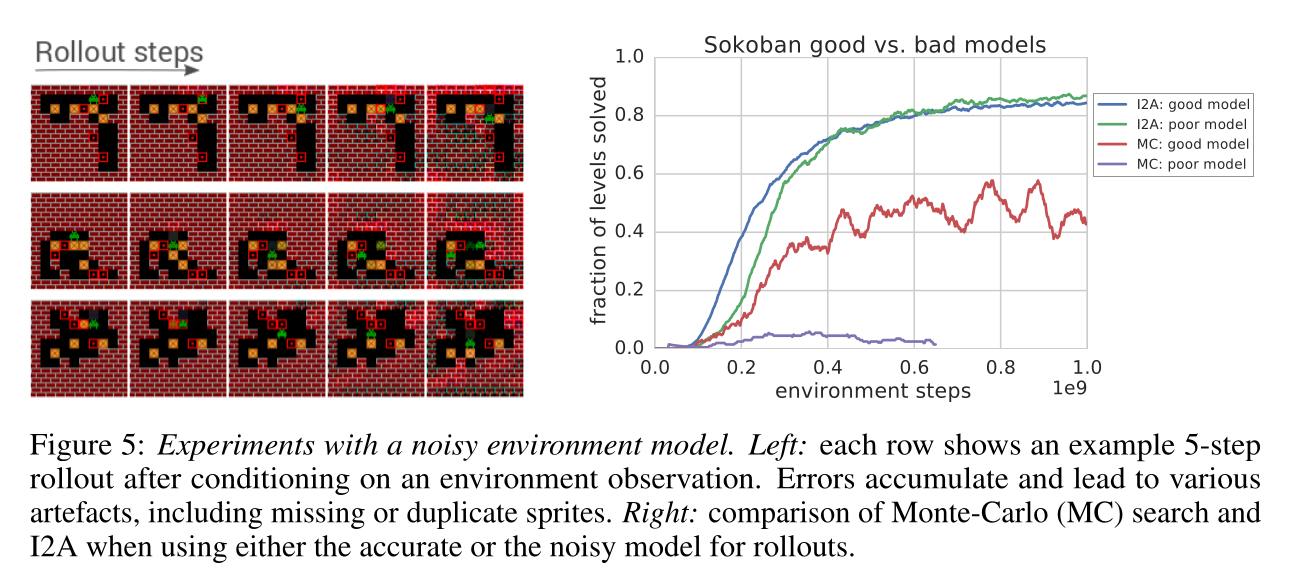
The model does not even have to be perfect: the MF path can compensate for imperfections: