World models, Dreamer

World models

The core idea of world models (Ha and Schmidhuber, 2018) is to explicitly separate the world model (what will happen next) from the controller (how to act). The neural networks used in deep RL are usually small, as rewards do not contain enough information to train huge networks. However, unsupervised data (without any label nor reward) is plenty and could be leveraged to learn useful representations. A huge world model can be efficiently trained by self-supervised / unsupervised methods, while a small controller should not need too many trials if its input representations are good.

Ha and Schmidhuber (2018) used the Vizdoom Take Cover environment (http://vizdoom.cs.put.edu.pl/) to demonstrate the power of world models, as well as a car racing environment.

Tip

For a detailed explanation of world models, refer to:

https://worldmodels.github.io/

The videos embedded here come from this page.

Architecture

The architecture of World Models is composed of three modules trained in succession:

1. The Vision module V,
2. The Memory module M,
3. The Controller module C.

Figure 23.1: Architecture of world models. Source: https://worldmodels.github.io/

Vision module

The vision module V is the encoder of a variational autoencoder (VAE), trained on single frames of the game (obtained using a random policy). The resulting latent vector \mathbf{z}_t contains a compressed representation of the frame \mathbf{o}_t.

Figure 23.2: Vision module. Source: https://worldmodels.github.io/

Memory module

The sequence of latent representations \mathbf{z}_0, \ldots \mathbf{z}_t in a game is fed to a LSTM layer (RNN) together with the actions a_t to compress what happens over time.

A Mixture Density Network (MDN, Bishop (1994)) is used to predict the distribution of the next latent representations P(\mathbf{z}_{t+1} | a_t, \mathbf{h}_t, \ldots \mathbf{z}_t). In short, MDN allows to perform probabilistic regression, but predicting both the mean and the variance of the data, instead of just its mean as in vanilla least sqaures regression. Most MDN methods use a mixture of Gaussian distributions to model the target distribution.

Figure 23.3: Memory module. Source: https://worldmodels.github.io/

RNN-MDN

The RNN-MDN architecture has been used successfully in the past for sequence generation problems such as generating handwriting and sketches (Sketch-RNN, Ha and Eck (2017)).

Check a demo here: https://magenta.tensorflow.org/sketch-rnn-demo

Controller module

The last step is the controller. It takes a latent representation \mathbf{z}_t and the current hidden state of the LSTM \mathbf{h}_t as inputs and selects an action linearly:

a_t = \text{tanh}(W \, [\mathbf{z}_t, \mathbf{h}_t ] + b)

A RL actor cannot get simpler as that…

Figure 23.4: Controller module. Source: https://worldmodels.github.io/

The controller is not even trained with RL: it uses a genetic algorithm, the Covariance-Matrix Adaptation Evolution Strategy (CMA-ES, Hansen and Ostermeier (2001)), to find the output weights that maximize the returns. The world model is trained by classical self-supervised learning using a random agent before learning, while the controller is simply evolved using a black-box optimizer.

World models

Algorithm:

1. Collect 10,000 rollouts from a random policy.

2. Train VAE (V) to encode each frame into a latent vector \mathbf{z} \in \mathcal{R}^{32}.

3. Train MDN-RNN (M) to model P(\mathbf{z}_{t+1} | a_t, \mathbf{h}_t, \ldots \mathbf{z}_t).

4. Evolve Controller (C) to maximize the expected cumulative reward of a rollout.

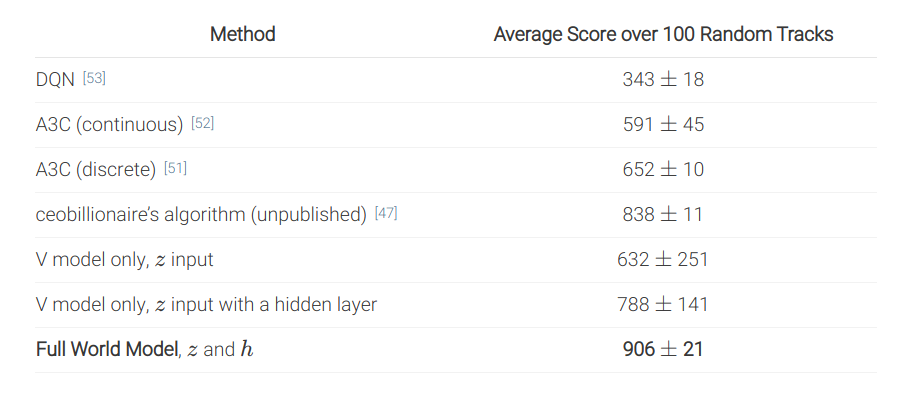
For the car racing environment, the repartition of the number of weights clearly shows that the complexity of the model lies in the world model, not the controller:

Parameters for car racing:

Model	Parameter Count
VAE	4,348,547
MDN-RNN	422,368
Controller	867

Results

Performance in car racing:

Below is the input of the VAE and the reconstruction. The reconstruction does not have to be perfect as long as the latent space is informative.

Having access to a full rollout of the future leads to more stable driving:

Figure 23.5: Performance of World models on the car racing environemnt. Source: https://worldmodels.github.io/

In summary, the world model V+M is learned offline with a random agent, using self-supervised learning, while the controller C has few weights (1000) and can be trained by evolutionary algorithms, not even RL. The network can even learn by playing entirely in its own imagination, as the world model can be applied on itself and predict all future frames. It just needs to additionally predict the reward. After that, the learned policy can be transferred to the real environment.

Deep Planning Network - PlaNet

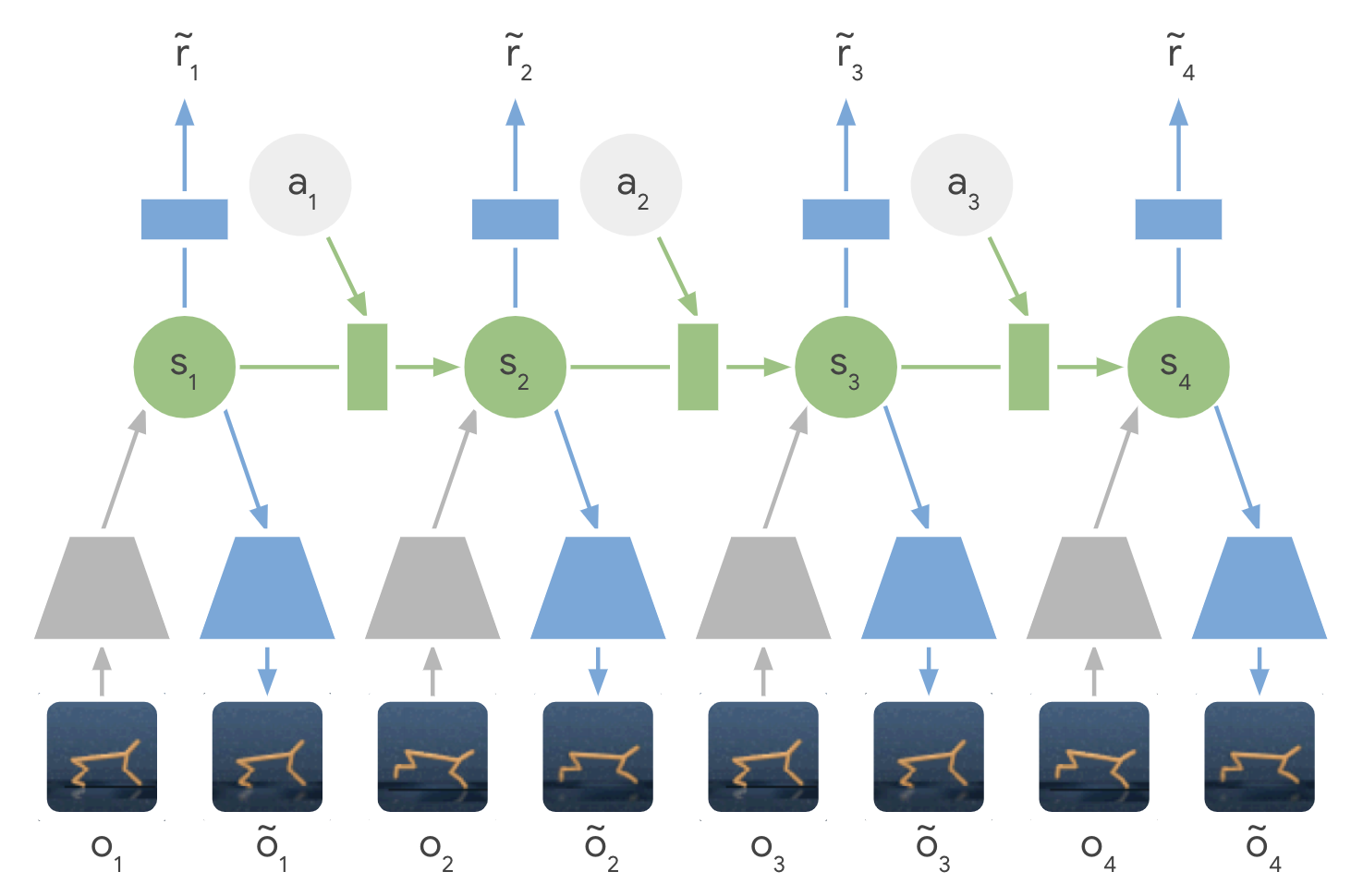
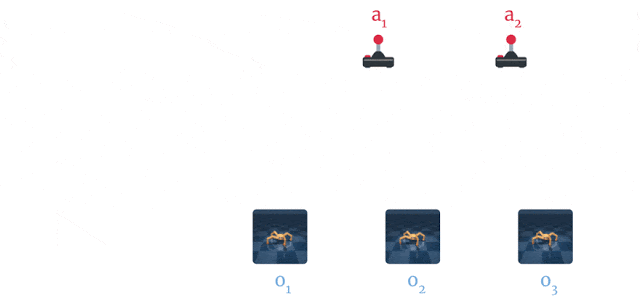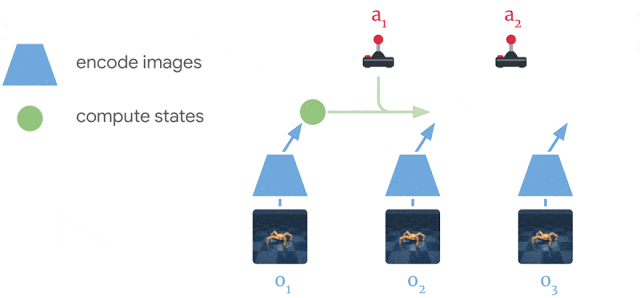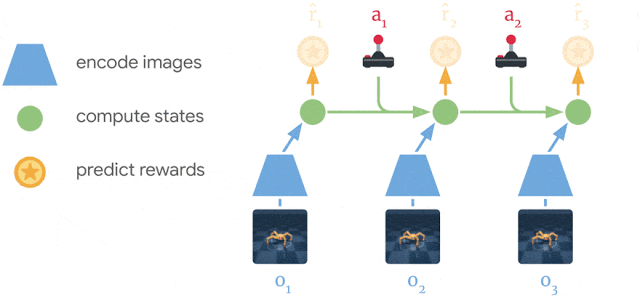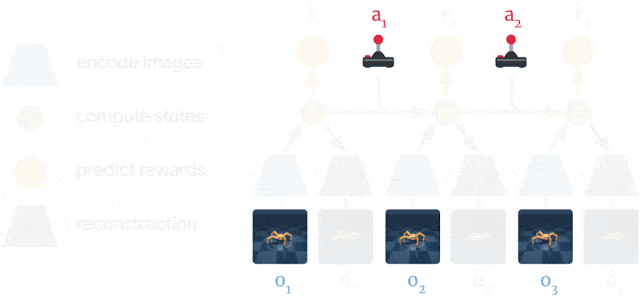
PlaNet (Hafner et al., 2019) extends the idea of World models by learning the model together with the policy (end-to-end). It learns a latent dynamics model that takes the past observations o_t into account (needed for POMDPs):

s_{t}, r_{t+1}, \hat{o}_t = f(o_t, a_t, s_{t-1})

and plans in the latent space using multiple rollouts:

a_t = \text{arg}\max_a \mathbb{E}[R(s_t, a, s_{t+1}, \ldots)]

Training

Figure 23.6: Latent dynamics model of PlaNet. Source: https://planetrl.github.io/

The latent dynamics model is a sequential variational autoencoder learning concurrently:

1. An encoder from the observation o_t to the latent space s_t.

q(s_t | o_t)

2. A decoder from the latent space to the reconstructed observation \hat{o}_t.

p(\hat{o}_t | s_t)

3. A transition model to predict the next latent representation given an action.

p(s_{t+1} | s_t, a_t)

4. A reward model predicting the immediate reward.

p(r_t | s_t)

Training sequences (o_1, a_1, o_2, \ldots, o_T) can be generated off-policy (e.g. from demonstrations) or on-policy. The loss function to train this recurrent state-space model (RSSM), which has a stochastic component in the encoder (VAE), and has to compensate for latent overshooting (i.e. to enforce consistency between one-step and multi-step predictions in the latent space), is slightly complicated and is not explained here.

Figure 23.7: Training the latent dynamics model of PlaNet. Source: https://ai.googleblog.com/2020/03/introducing-dreamer-scalable.html

Inference

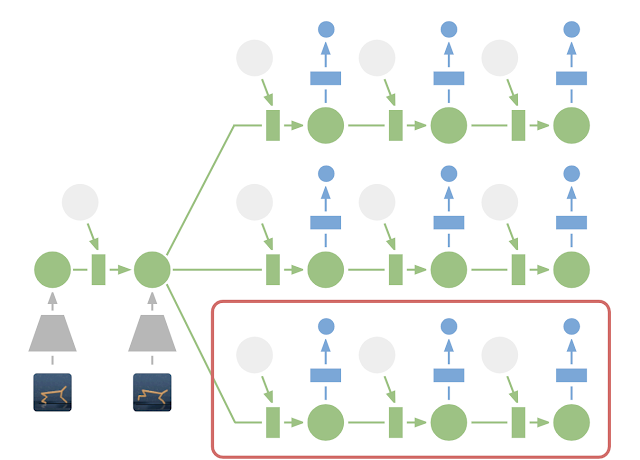
From a single observation o_t encoded into s_t, we can generate 10000 rollouts using random sampling. In these rollouts, the action sequences are varied randomly, generating as many random sequences as needed. The return of each rollout can be estimated using the reward model. A belief over the action sequences is updated using the cross-entropy method (CEM, Szita and Lörincz (2006)) in order to restrict the search.

After the 10000 rollouts are executed (in imagination), the sequence with the highest return is selected and its first action is executed. At the next time step, planning starts from scratch: this is the key idea of Model Predictive Control. There is no actor in PlaNet, only a transition model used for planning. The reason PlaNet works is that planning is done in the latent space, hich has a much lower dimensionality than the observations (e.g. images).

Source: https://ai.googleblog.com/2019/02/introducing-planet-deep-planning.html

Results

Planet learns continuous Mujoco image-based control problems in 2000 episodes, where D4PG needs 50 times more.

The latent dynamics model can learn 6 control tasks at the same time. As there is no actor, but only a planner, the same network can control all agents!

Figure 23.8: Top row: agent behavior on the 6 Mujoco tasks. Bottom row: predcited frames by the agent. Source: https://ai.googleblog.com/2019/02/introducing-planet-deep-planning.html

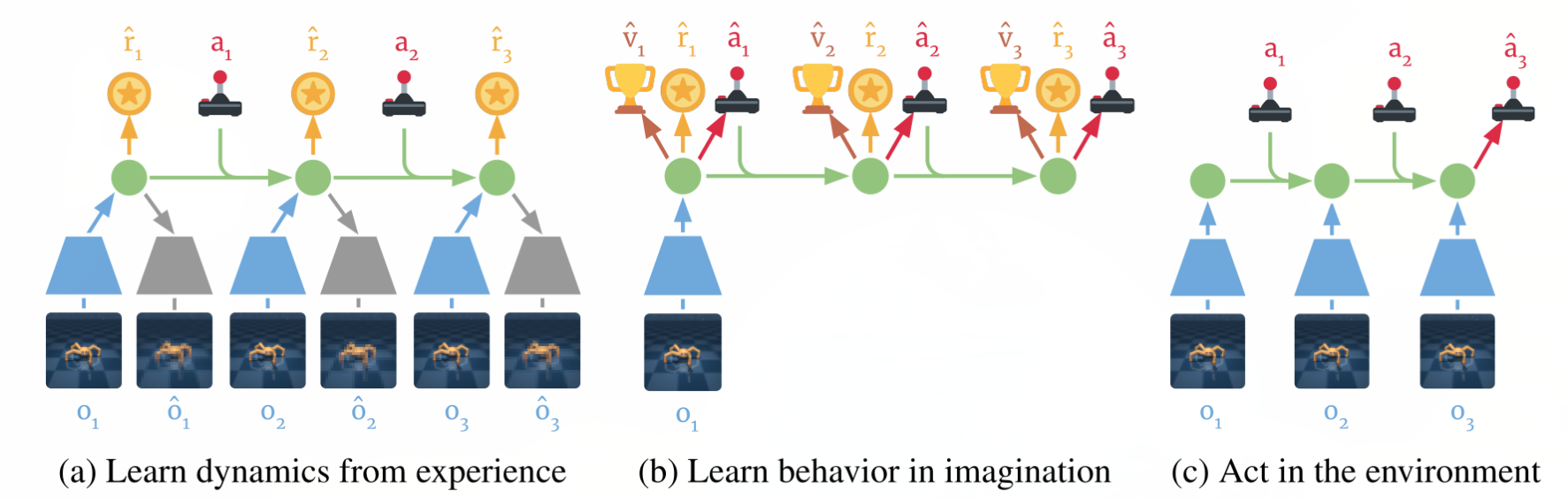
Dreamer

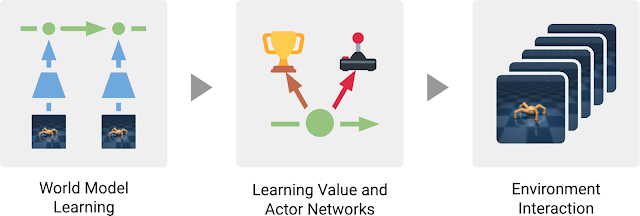
Dreamer (Hafner et al., 2020) extends the idea of PlaNet by additionally training an actor instead of using a MPC planner. The latent dynamics model is the same RSSM architecture. Training a “model-free” actor on imaginary rollouts instead of MPC planning should reduce the computational cost at inference time.

Figure 23.9: Dreamer first learns the World model (RSSM), then trains a model-free agent in its imagination to maximize the rewards, before being used to interact with the environment. Source: https://ai.googleblog.com/2020/03/introducing-dreamer-scalable.html

The latent dynamics model is the same as in PlaNet, learning from past experiences.

Figure 23.10: Latent dynamics model of Dreamer, exactly the same as PlaNet. Source: https://ai.googleblog.com/2020/03/introducing-dreamer-scalable.html

The behavior module learns to predict the value of a state V_\varphi(s) and the policy \pi_\theta(s) (actor-critic). It is trained in imagination in the latent space using the reward model for the immediate rewards (to compute returns) and the transition model for the next states.

Figure 23.11: The actor-critic agent is trained in imagination using rollouts generated by the RSSM model. Source: https://ai.googleblog.com/2020/03/introducing-dreamer-scalable.html

The current observation o_t is encoded into a state s_t, the actor selects an action a_t, the transition model predicts s_{t+1}, the reward model predicts r_{t+1}, the critic predicts V_\varphi(s_t). At the end of the sequence, we apply backpropagation-through-time to train the actor and the critic.

The critic V_\varphi(s_t) is trained on the imaginary sequence (s_t, a_t, r_{t+1}, s_{t+1}, \ldots, s_T) to minimize the prediction error with the \lambda-return:

R^\lambda_t = (1 - \lambda) \, \sum_{n=1}^{T-t-1} \lambda^{n-1} \, R^n_t + \lambda^{T-t-1} \, R_t

The actor \pi_\theta(s_t, a_t) is trained on the sequence to maximize the sum of the value of the future states:

\mathcal{J}(\theta) = \mathbb{E}_{s_t, a_t \sim \pi_\theta} [\sum_{t'=t}^T V_\varphi(s_{t'})]

The main advantage of training an actor is that we need only one rollout when training it: backpropagation maximizes the expected returns. When acting, we just need to encode the history of the episode in the latent space, and the actor becomes model-free!

Figure 23.12: Complete Dreamer architecture. Source: https://ai.googleblog.com/2020/03/introducing-dreamer-scalable.html

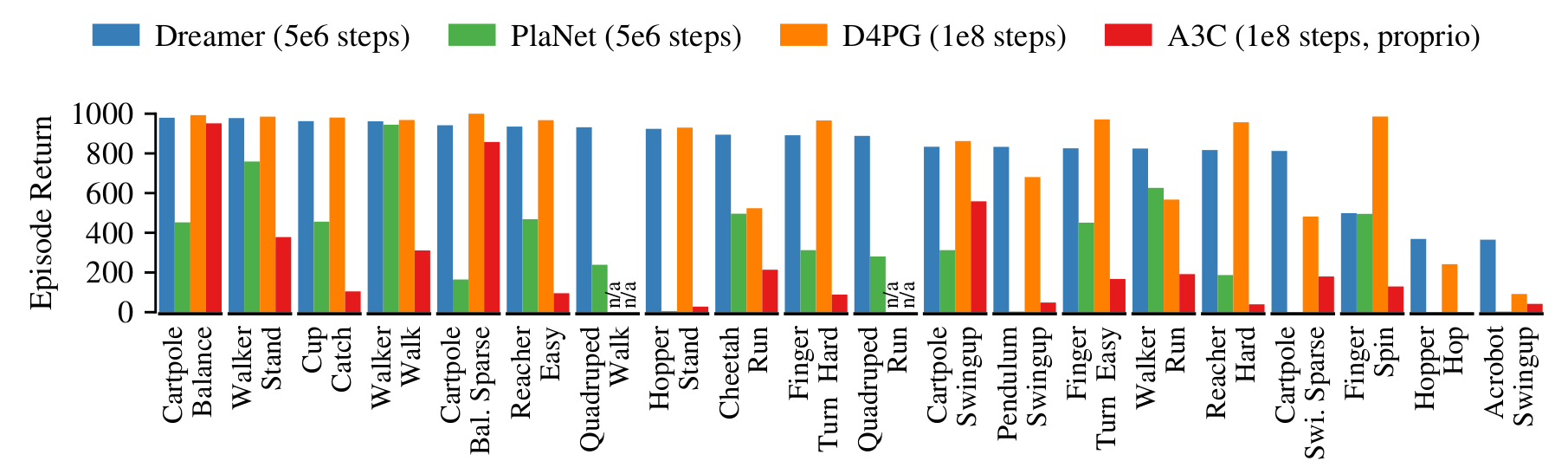
Dreamer beats model-free and model-based methods on 20 continuous control tasks.

Figure 23.13: Results of Dreamer on various Mujoco tasks, compared to SotA control methods. Source: https://ai.googleblog.com/2020/03/introducing-dreamer-scalable.html

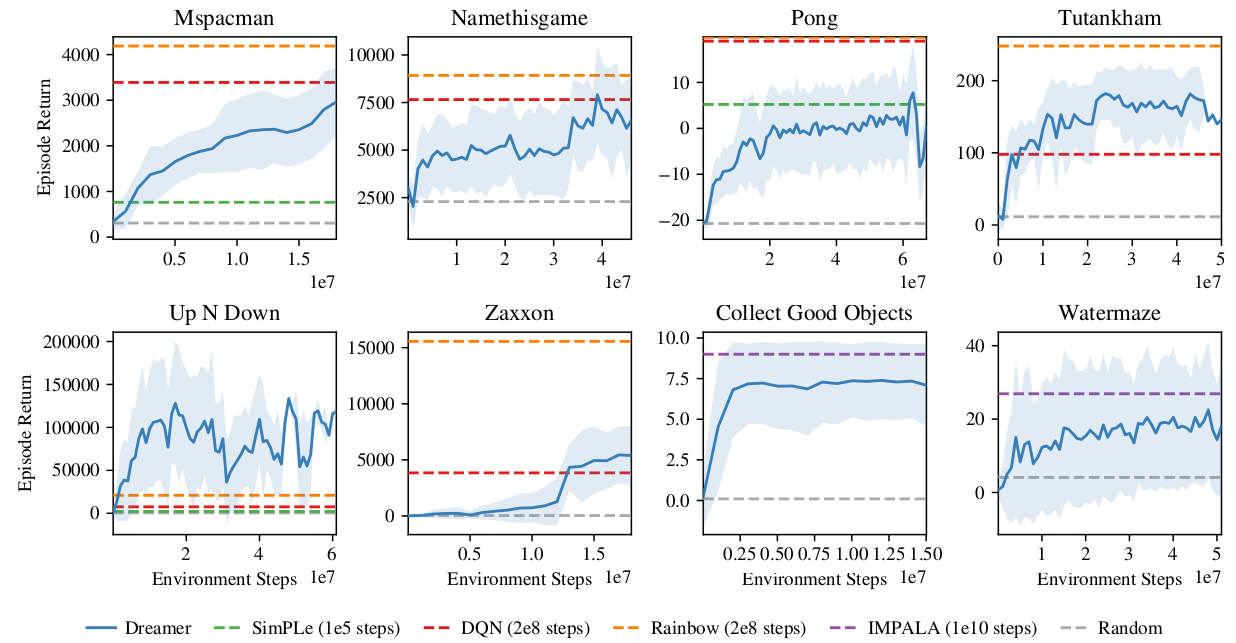
It also learns Atari and Deepmind lab video games, sometimes on par with Rainbow or IMPALA!

Figure 23.14: Results of Dreamer on Atari gameSource: https://dreamrl.github.io/

A recent extension of Dreamer, DayDreamer (Wu et al., 2022), allows physical robots to learn complex tasks in a few hours.

DayDreamer. Source: Wu et al. (2022) and https://danijar.com/daydreamer

Bishop, C. M. (1994). Mixture Density Networks. Birmingham, UK: Neural Computing Research Group, Aston University Available at: https://publications.aston.ac.uk/id/eprint/373/1/NCRG_94_004.pdf [Accessed November 12, 2024].

Ha, D., and Eck, D. (2017). A Neural Representation of Sketch Drawings. Available at: http://arxiv.org/abs/1704.03477 [Accessed January 17, 2021].

Ha, D., and Schmidhuber, J. (2018). World Models. doi:10.5281/zenodo.1207631.

Hafner, D., Lillicrap, T., Ba, J., and Norouzi, M. (2020). Dream to Control: Learning Behaviors by Latent Imagination. Available at: http://arxiv.org/abs/1912.01603 [Accessed March 24, 2020].

Hafner, D., Lillicrap, T., Fischer, I., Villegas, R., Ha, D., Lee, H., et al. (2019). Learning Latent Dynamics for Planning from Pixels. Available at: http://arxiv.org/abs/1811.04551 [Accessed January 24, 2020].

Hansen, N., and Ostermeier, A. (2001). Completely Derandomized Self-Adaptation in Evolution Strategies. Evolutionary Computation 9, 159–195. doi:10.1162/106365601750190398.

Szita, I., and Lörincz, A. (2006). Learning Tetris Using the Noisy Cross-Entropy Method. Neural Computation 18, 2936–2941. doi:10.1162/neco.2006.18.12.2936.

Wu, P., Escontrela, A., Hafner, D., Goldberg, K., and Abbeel, P. (2022). DayDreamer: World Models for Physical Robot Learning. doi:10.48550/arXiv.2206.14176.