1. Artificial neural networks¶
Slides: pdf
1.1. Multi-layer perceptron¶
A Multi-Layer Perceptron (MLP) or feedforward neural network is composed of:
an input layer for the input vector \(\mathbf{x}\)
one or several hidden layers allowing to project non-linearly the input into a space of higher dimensions \(\mathbf{h}_1, \mathbf{h}_2, \mathbf{h}_3, \ldots\).
an output layer for the output \(\mathbf{y}\).
Fig. 1.29 Multi-layer perceptron with one hidden layer.¶
If there is a single hidden layer \(\mathbf{h}\) (shallow network), it corresponds to the feature space. Each layer takes inputs from the previous layer. If the hidden layer is adequately chosen, the output neurons can learn to replicate the desired output \(\mathbf{t}\).
1.1.1. Fully-connected layer¶
The operation performed by each layer can be written in the form of a matrix-vector multiplication:
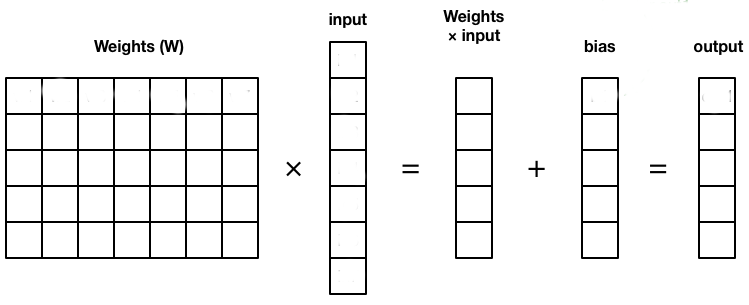
Fig. 1.30 Fully-connected layer.¶
Fully-connected layers (FC) transform an input vector \(\mathbf{x}\) into a new vector \(\mathbf{h}\) by multiplying it by a weight matrix \(W\) and adding a bias vector \(\mathbf{b}\). A non-linear activation function transforms each element of the net activation.
1.1.2. Activation functions¶
Here are some of the most useful activation functions in a MLP.
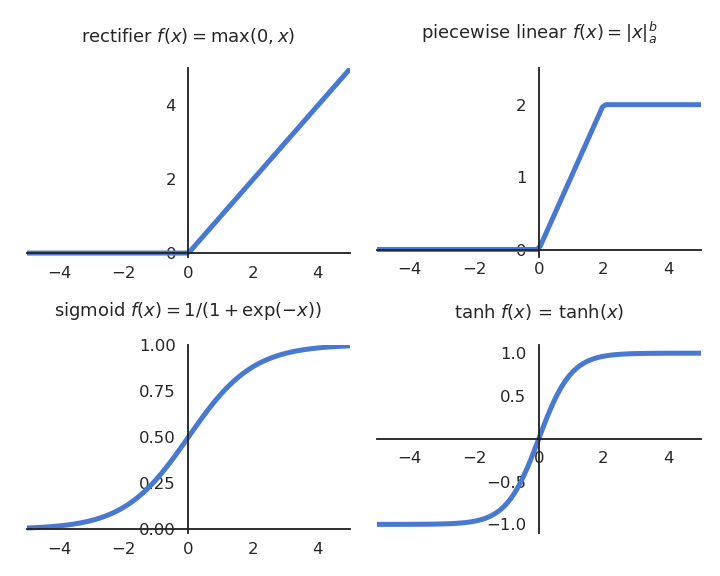
Fig. 1.31 Some classical activation functions in MLPs.¶
Threshold function (output is binary)
Logistic / sigmoid function (output is continuous and bounded between 0 and 1)
Hyperbolic function (output is continuous and bounded between -1 and 1)
Rectified linear function - ReLU (output is continuous and positive).
Parametric Rectifier Linear Unit - PReLU (output is continuous and unbounded).
Fig. 1.32 ReLU vs. PReLU activation functions.¶
For classification problems, the softmax activation function can be used in the output layer to make sure that the sum of the outputs \(\mathbf{y} = \{y_j\}\) over all output neurons is one.
The higher the net activation \(\text{net}_j\), the higher the probability that the example belongs to class \(j\). Softmax is not per se a transfer function (not local to each neuron), but the idea is similar.
Note
Why not use the linear function \(f(x) = x\) in the hidden layer?
We would have:
so the equivalent function would be linear…
Remember Cover’s theorem:
A complex pattern-classification problem, cast in a high dimensional space non-linearly, is more likely to be linearly separable than in a low-dimensional space, provided that the space is not densely populated.
In practice it does not matter how non-linear the function is (e.g PReLU is almost linear), but there must be at least one non-linearity.
1.1.3. Loss function¶
We have a training set \mathcal{D} composed of N input/output pairs \((\mathbf{x}_i, \mathbf{t}_i)_{i=1..N}\). What are the free parameters \(\theta\) (weights \(W^1, W^2\) and biases \(\textbf{b}^1, \textbf{b}^2\)) making the prediction \(\mathbf{y}\) as close as possible from the desired output \(\mathbf{t}\)?
We define a loss function \(\mathcal{L}(\theta)\) of the free parameters which should be minimized:
For regression problems, we take the mean square error (mse):
For classification problems, we take the cross-entropy or negative log-likelihood on a softmax output layer:
1.1.4. Optimizer¶
To minimize the chosen loss function, we are going to use stochastic gradient descent iteratively until the network converges:
We will see later that other optimizers than SGD can be used. The question is now how to compute efficiently these gradients w.r.t all the weights and biases. The algorithm to achieve this is called backpropagation [Rumelhart et al., 1986], which is simply a smart implementation of the chain rule.
Note
[Rumelhart et al., 1986] did not actually invent backpropagation but merely popularized it in an article in Nature. Seppo Linnainmaa published the reverse mode of automatic differentiation in his Master thesis back in 1970 [Linnainmaa, 1970] and Paul Werbos applied it to deep neural networks in 1982 [Werbos, 1982].
For a controversy about the origins of backpropagation and who should get credit for deep learning, see this strongly-worded post by Jürgen Schmidhuber:
https://people.idsia.ch/~juergen/scientific-integrity-turing-award-deep-learning.html
1.2. Backpropagation¶
1.2.1. Backpropagation on a shallow network¶
A shallow MLP computes:
The chain rule gives us for the parameters of the output layer:
and for the hidden layer:
If we can compute all these partial derivatives / gradients individually, the problem is solved.
We have already seen for the linear algorithms that the derivative of the loss function w.r.t the net activation of the output \(\textbf{net}_\mathbf{y}\) is proportional to the prediction error \(\mathbf{t} - \mathbf{y}\):
mse for regression:
cross-entropy using a softmax output layer:
\(\mathbf{\delta_y} = - \dfrac{\partial \mathcal{l}(\theta)}{\partial \textbf{net}_\mathbf{y}}\) is called the output error. The output error is going to appear in all partial derivatives, i.e. in all learning rules. The backpropagation algorithm is sometimes called backpropagation of the error.
We now have everything we need to train the output layer:
As \(\textbf{net}_\mathbf{y} = W^2 \, \mathbf{h} + \mathbf{b}^2\), we get for the cross-entropy loss:
i.e. exactly the same delta learning rule as a softmax linear classifier or multiple linear regression using the vector \(\mathbf{h}\) as an input.
Let’s now note \(\mathbf{\delta_h}\) the hidden error, i.e. minus the gradient of the loss function w.r.t the net activation of the hidden layer:
Using this hidden error, we can compute the gradients w.r.t \(W^1\) and \(\mathbf{b}^1\):
As \(\textbf{net}_\mathbf{h} = W^1 \, \mathbf{x} + \mathbf{b}^1\), we get:
If we know the hidden error \(\mathbf{\delta_h}\), the update rules for the input weights \(W^1\) and \(\mathbf{b}^1\) also take the form of the delta learning rule:
This is the classical form eta * error * input. All we need to know is the backpropagated error \(\mathbf{\delta_h}\) and we can apply the delta learning rule!
The backpropagated error \(\mathbf{\delta_h}\) is a vector assigning an error to each of the hidden neurons:
As :
we obtain:
If \(\mathbf{h}\) and \(\mathbf{\delta_h}\) have \(K\) elements and \(\mathbf{y}\) and \(\mathbf{\delta_y}\) have \(C\) elements, the matrix \(W^2\) is \(C \times K\) as \(W^2 \times \mathbf{h}\) must be a vector with \(C\) elements. \((W^2)^T \times \mathbf{\delta_y}\) is therefore a vector with \(K\) elements, which is then multiplied element-wise with the derivative of the transfer function to obtain \(\mathbf{\delta_h}\).
Backpropagation for a shallow MLP
Fig. 1.33 Shallow MLP.¶
For a shallow MLP with one hidden layer:
the output error:
is backpropagated to the hidden layer:
what allows to apply the delta learning rule to all parameters:
The usual transfer functions are easy to derive (that is why they are chosen…).
Threshold and sign functions are not differentiable, we simply consider the derivative is 1.
The logistic or sigmoid function has the nice property that its derivative can be expressed as a function of itself:
The hyperbolic tangent function too:
ReLU is even simpler:
1.2.2. Backpropagation at the neuron level¶
Let’s have a closer look at what is backpropagated using single neurons and weights. The output neuron \(y_k\) computes:
All output weights \(W^2_{jk}\) are updated proportionally to the output error of the neuron \(y_k\):
This is possible because we know the output error directly from the data \(t_k\).
The hidden neuron \(h_j\) computes:
We want to learn the hidden weights \(W^1_{ij}\) using the delta learning rule:
but we do not know the ground truth of the hidden neuron in the data:
We need to estimate the backpropagated error using the output error. If we omit the derivative of the transfer function, the backpropagated error for the hidden neuron \(h_j\) is:
The backpropagated error is an average of the output errors \(\delta_{{y}_k}\), weighted by the output weights between the hidden neuron \(h_j\) and the output neurons \(y_k\).
The backpropagated error is the contribution of each hidden neuron \(h_j\) to the output error:
If there is no output error, there is no hidden error.
If a hidden neuron sends strong weights \(|W^2_{jk}|\) to an output neuron \(y_k\) with a strong prediction error \(\delta_{{y}_k}\), this means that it participates strongly to the output error and should learn from it.
If the weight \(|W^2_{jk}|\) is small, it means that the hidden neuron does not take part in the output error.
1.2.3. Universal approximation theorem¶
Universal approximation theorem
Cybenko, 1989
Let \(\varphi()\) be a nonconstant, bounded, and monotonically-increasing continuous function. Let \(I_{m_0}\) denote the \(m_0\)-dimensional unit hypercube \([0,1]^{m_0}\). The space of continuous functions on \(I_{m_0}\) is denoted by \(C(I_{m_0})\). Then, given any function \(f \in C(I_{m_0})\) and \(\epsilon > 0\), there exists an integer \(m_1\) and sets of real constants \(\alpha_i, b_i\) and \(w_{ij} \in \Re\), where \(i = 1, ..., m_1\) and \(j = 1, ..., m_0\) such that we may define:
as an approximate realization of the function f; that is,
for all \(x \in I_m\).
This theorem shows that for any input/output mapping function \(f\) in supervised learning, there exists a MLP with \(m_1\) neurons in the hidden layer which is able to approximate it with a desired precision!
The universal approximation theorem only proves the existence of a shallow MLP with \(m_1\) neurons in the hidden layer that can approximate any function, but it does not tell how to find this number. A rule of thumb to find this number is that the generalization error is empirically close to:
where \(\text{VC}_{\text{dim}}(\text{MLP})\) is the total number of weights and biases in the model, and \(N\) the number of training samples.
The more neurons in the hidden layer, the better the training error, but the worse the generalization error (overfitting). The optimal number should be found with cross-validation methods. For most functions, the optimal number \(m_1\) is high and becomes quickly computationally untractable. We need to go deep!
1.2.4. Backpropagation on a deep neural network¶
A MLP with more than one hidden layer is a deep neural network.
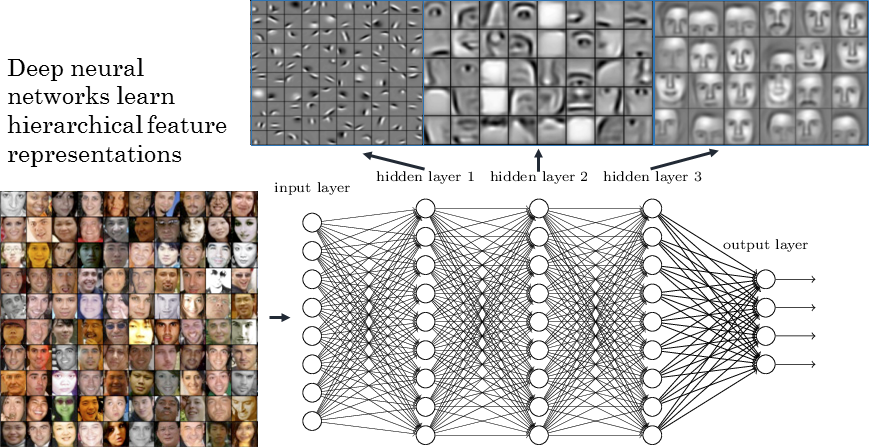
Fig. 1.34 Deep network extract progressively more complex features.¶
Backpropagation still works if we have many hidden layers \(\mathbf{h}_1, \ldots, \mathbf{h}_n\):
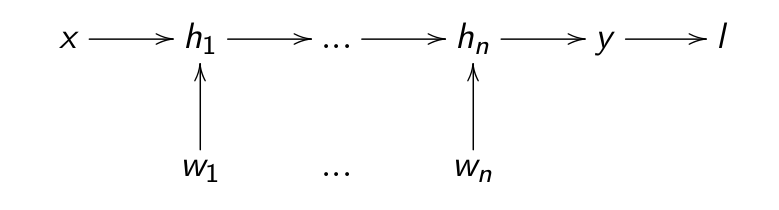
Fig. 1.35 Forward pass. Source: David Silver https://icml.cc/2016/tutorials/deep_rl_tutorial.pdf¶
If each layer is differentiable, i.e. one can compute its gradient \(\frac{\partial \mathbf{h}_{k}}{\partial \mathbf{h}_{k-1}}\), we can chain backwards each partial derivatives to know how to update each layer.
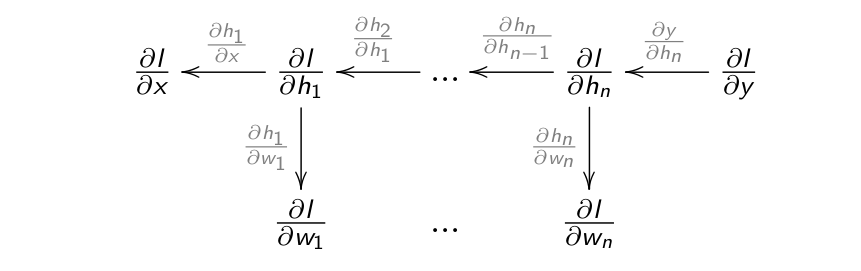
Fig. 1.36 Backpropagation pass. Source: David Silver https://icml.cc/2016/tutorials/deep_rl_tutorial.pdf¶
Backpropagation is simply an efficient implementation of the chain rule: the partial derivatives are iteratively reused in the backwards phase.
A fully connected layer transforms an input vector \(\mathbf{h}_{k-1}\) into an output vector \(\mathbf{h}_{k}\) using a weight matrix \(W^k\), a bias vector \(\mathbf{b}^k\) and a non-linear activation function \(f\):
The gradient of its output w.r.t the input \(\mathbf{h}_{k-1}\) is (using the chain rule):
The gradients of its output w.r.t the free parameters \(W^k\) and \(\mathbf{b}_{k}\) are:
A fully connected layer \(\mathbf{h}_{k} = f(W^k \, \mathbf{h}_{k-1} + \mathbf{b}^k)\) receives the gradient of the loss function w.r.t. its output \(\mathbf{h}_{k}\) from the layer above:
It adds to this gradient its own contribution and transmits it to the previous layer:
It then updates its parameters \(W^k\) and \(\mathbf{b}_{k}\) with:
Training a deep neural network with backpropagation
A feedforward neural network is an acyclic graph of differentiable and parameterized layers.
The backpropagation algorithm is used to assign the gradient of the loss function \(\mathcal{L}(\theta)\) to each layer using backward chaining:
Stochastic gradient descent is then used to update the parameters of each layer:
1.3. Example of a shallow network¶
Let’s try to solve this non-linear binary classification problem:
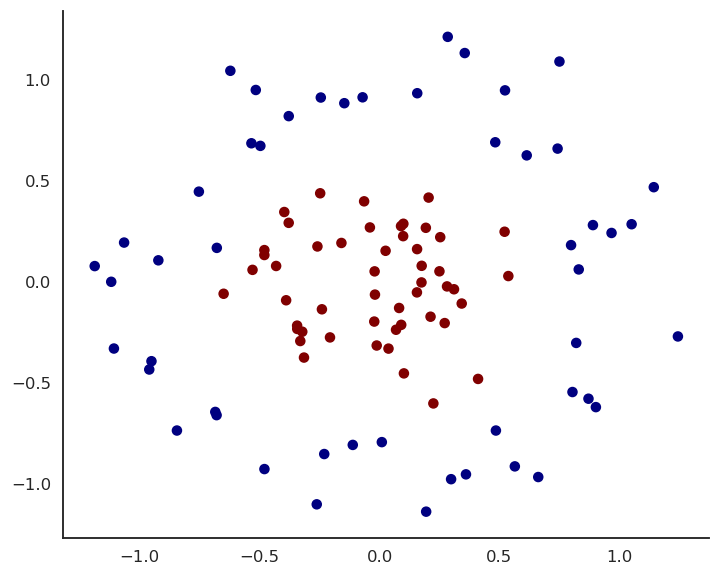
Fig. 1.37 Non-linearly separable dataset.¶
We can create a shallow MLP with:
Two input neurons \(x_1, x_2\) for the two input variables.
Enough hidden neurons (e.g. 20), with a sigmoid or ReLU activation function.
One output neuron with the logistic activation function.
The cross-entropy (negative log-likelihood) loss function.
Fig. 1.38 Simple MLP for the non-linearly separable dataset.¶
We train it on the input data using the backpropagation algorithm and the SGD optimizer.
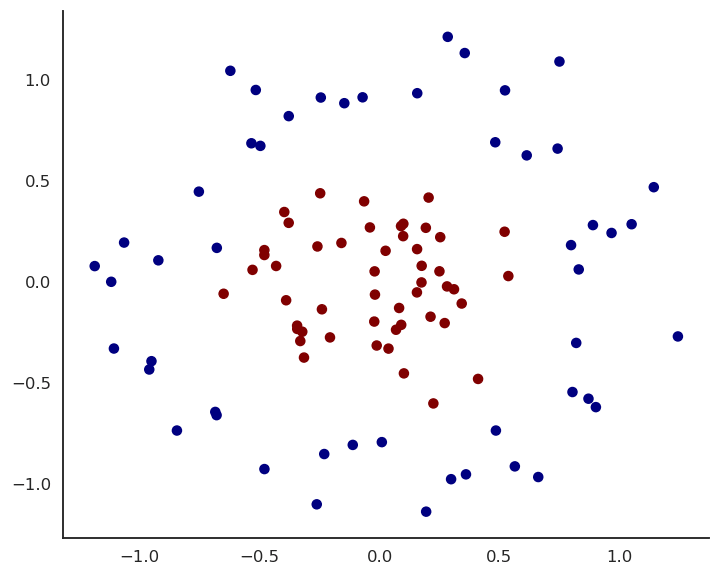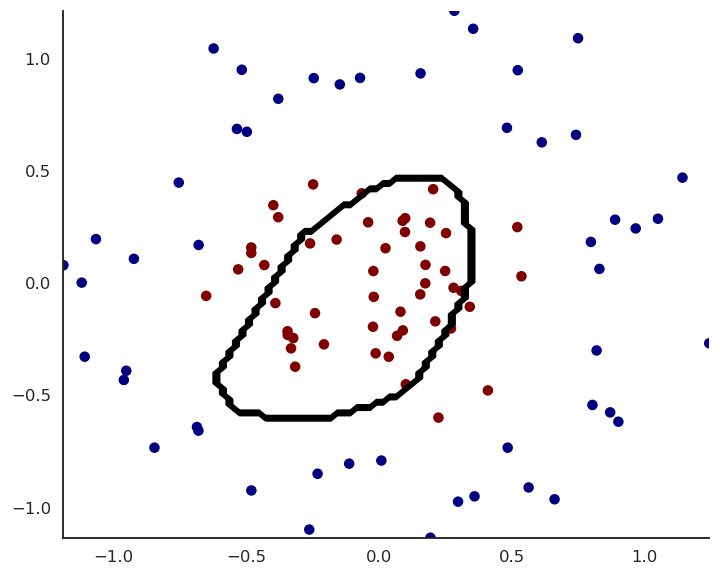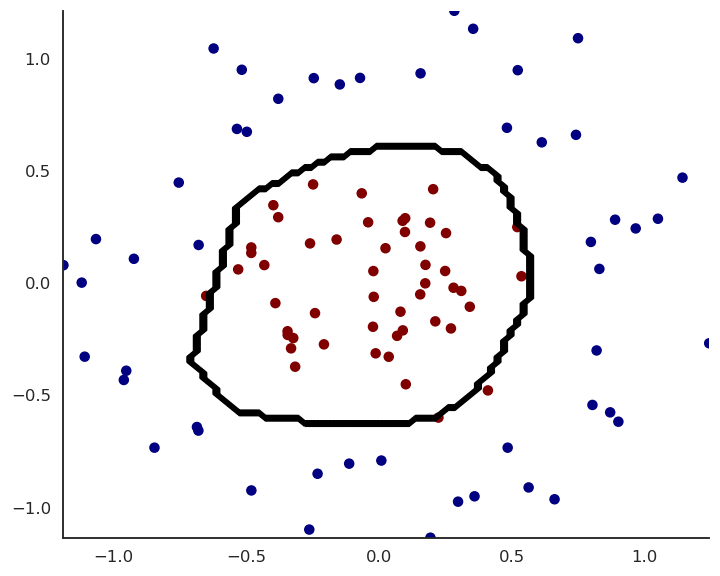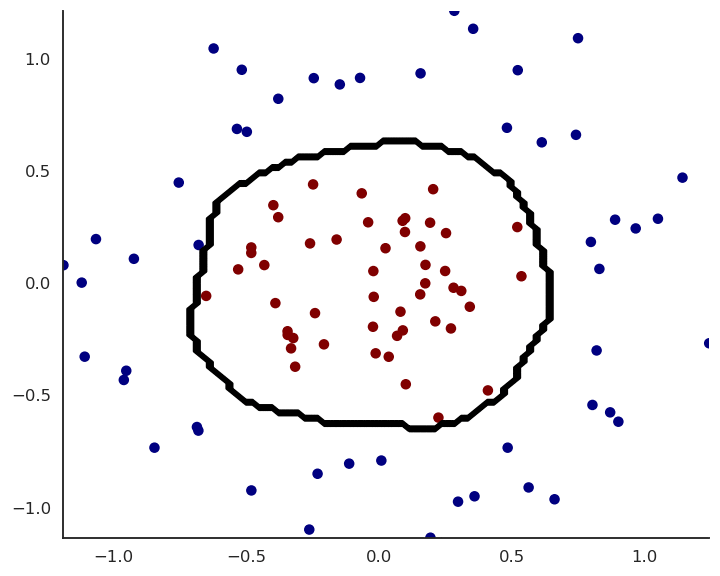
Fig. 1.39 Prediction after each epoch of training.¶
Experiment with this network live on https://playground.tensorflow.org/! You will implement this MLP with numpy during exercise 8.
Automatic differentiation Deep Learning frameworks
Current:
Tensorflow https://www.tensorflow.org/ released by Google in 2015 is one of the two standard DL frameworks.
Keras https://keras.io/ is a high-level Python API over tensorflow (but also theano, CNTK and MxNet) written by Francois Chollet.
PyTorch http://pytorch.org by Facebook is the other standard framework.
Historical:
Theano http://deeplearning.net/software/theano/ released by U Toronto in 2010 is the predecessor of tensorflow. Now abandoned.
Caffe http://caffe.berkeleyvision.org/ by U Berkeley was long the standard library for convolutional networks.
CNTK https://github.com/Microsoft/CNTK (Microsoft Cognitive Toolkit) is a free library by Microsoft!
MxNet https://github.com/apache/incubator-mxnet from Apache became the DL framework at Amazon.
Let’s implement the previous MLP using keras. We first need to generate the data using scikit-learn:
import sklearn.datasets
X, t = sklearn.datasets.make_circles(n_samples=100, shuffle=True, noise=0.15, factor=0.3)
We then import tensorflow:
import tensorflow as tf
The neural network is called a Sequential model in keras:
model = tf.keras.Sequential()
Creating a NN is simply stacking layers in the model. The input layer is just a placeholder for the data:
model.add( tf.keras.layers.Input(shape=(2, )) )
The hidden layer has 20 neurons, the ReLU activation and takes input from the previous layer:
model.add(
tf.keras.layers.Dense(
20, # Number of hidden neurons
activation='relu' # Activation function
)
)
The output layer has 1 neuron with the logistic/sigmoid activation function:
model.add(
tf.keras.layers.Dense(
1, # Number of output neurons
activation='sigmoid' # Soft classification
)
)
We now choose an optimizer (SGD) with a learning rate \(\eta = 0.001\):
optimizer = tf.keras.optimizers.SGD(lr=0.001)
We choose a loss function (binary cross-entropy, aka negative log-likelihood):
loss = tf.keras.losses.binary_crossentropy
We compile the model (important!) and tell it to track the accuracy of the model:
model.compile(
loss=loss,
optimizer=optimizer,
metrics=tf.keras.metrics.categorical_accuracy
)
Et voilà! The network has been created.
print(model.summary())
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 20) 60
_________________________________________________________________
dense_1 (Dense) (None, 1) 21
=================================================================
Total params: 81
Trainable params: 81
Non-trainable params: 0
_________________________________________________________________
None
We now train the model on the data for 100 epochs using a batch size of 10 and wait for it to finish:
model.fit(X, t, batch_size=10, nb_epoch=100)
With keras (and the other automatic differentiation frameworks), you only need to define the structure of the network. The rest (backpropagation, SGD) is done automatically. To make predictions on new data, just do:
model.predict(X_test)